Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 10
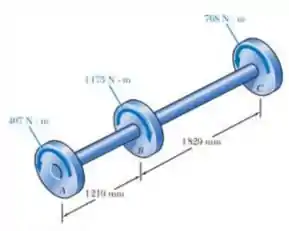
Os eixos do conjunto de polias mostrado na figura devem ser redimensionados. Sabendo que a tensão de cisalhamento admissível em cada eixo é de 58,6 MPa, determine o menor diâmetro admissível para (a) o eixo AB. (b) o eixo BC.
Passo 1
Fala aí gurizada tudo belezinha? O enunciado pede que a gente determine o menor diâmetro admissível para ambos os eixos, vamos começar pelo eixo AB, considerando o torque no valor de
Onde:
Passo 2
Então agora seguimos para o eixo BC!
Onde:
Resposta
Exercícios de Livros Relacionados
O eixo maciço com 60mm de diâmetro está sujeito aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine a tensão de cisalhamento nos pontos A e B e trace um rascunho da
Um eixo é feito de uma liga de aço com tensão de cisalhamento admissível τ a d m = 84MPa . Se o diâmetro do eixo for 37,5mm , determine o torque máximo T que pode ser transmitido. Qual seria o torque
O eixo tem diâmetro externo de 32mm e diâmetro interno de 25mm . Se for submetido aos torques mostrados na figura, faça o gráfico da distribuição de tensão de cisalhamento que age ao longo de uma linh
O eixo maciço de alumínio tem diâmetro de 50mm e tensão de cisalhamento admissível τ a d m = 6MPa . Determine o maior torque T 1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros ca
O eixo maciço é submetido aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine o diâmetro d exigido para o eixo se a tensão de cisalhamento admissível para o material