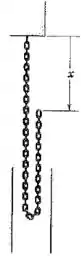
A extremidade livre da corrente de elos de comprimento total e massa por unidade de comprimento é liberada a partir do repouso em . Determine a força na extremidade fixa e a tração na corrente na extremidade inferior da parte sem movimento em termos de . Encontre também a perda total de energia quando .
Passo 1
Vamos começar olhando para parte livre da corrente. Essa parte está em queda livre, de forma que sua aceleração é simplesmente .
Mas a aceleração da parte livre da corda é simplesmente a derivada segunda da coordenada :
Como a velocidade inicial é nula, isso quer dizer que a velocidade da ponta da corrente é dada por:
Passo 2
Vamos tentar aproveitar esse resultado para escrever a tração na extremidade inferior da parte sem movimento. Podemos pensar nessa força como a que gera o “escoamento” da parte livre para a parte imóvel.
Nesse caso é a taxa de “escoamento” de massa vinda da parte livre. Olhando para a figura e usando a massa por unidade de comprimento , podemos escrever o seguinte:
E como a essa tensão precisa desacelerar essa massa:
E então:
Agora sim, podemos aproveitar o resultado do passo :
Passo 3
Agora precisamos encontrar a força que sustenta a parte imóvel da corrente. Já que essa parte não tem aceleração, a segunda lei de Newton dá o seguinte resultado:
Temos as seguintes forças verticais agindo: a tensão exercida pela outra parte da corda e o peso da porção imóvel voltados para baixo, e a força voltada para cima:
E olhando para a figura, podemos escrever uma expressão para a massa da porção imóvel:
E então:
Agora é só isolar :
Passo 4
Agora falta calcular qual é a perda total de energia quando , que é simplesmente o momento em que toda a corrente já “passou para o lado imóvel”.
Como a corrente parte do repouso e termina no repouso, podemos considerar que , então vamos nos concentrar na perda de energia potencial.
Vamos definir o zero da energia potencial como estando preso ao teto. A massa total da nossa corrente é:
E inicialmente (quando a corrente está “dobrada ao meio”) o centro de massa estava a uma altura:
Então:
No final do movimento (quando a corrente está totalmente esticada) o centro de massa está a um altura:
E a energia potencial é:
E então o módulo da variação total de energia potencial é:
E esse é o valor de que estávamos procurando:
Resposta
A força é , a tração é e a perda de energia é .