A haste esbelta AB de comprimento é ligada a um colar em B e repousa sobre um pequeno rolete localizado a uma distância horizontal da barra vertical sobre a qual o colar desliza. Sabendo que o coeficiente de atrito estático entre o colar e a barra vertical é 0,25 e desprezando o raio do rolete, determine o intervalo de valores de P para a qual o equilíbrio seja mantido quando e .
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para o colar supondo movimento para cima em B:
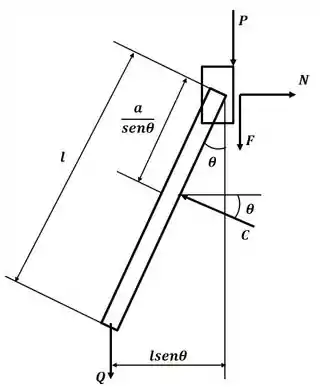
Sabemos que a força de atrito pode ser calculada por:
Passo 2
Agora vamos aplicar o somatório de momento em relação ao ponto B:
Agora podemos aplicar o somatório de forças na direção :
E, substituindo a expressão encontrada para :
Agora aplicando o somatório de forças na direção :
Substituindo os valores encontrados para N e C:
Simplificando a expressão, colocando Q em evidência e isolando P, temos:
Agora, substituindo os valores fornecidos no enunciado:
Passo 3
Agora, supondo que o movimento do colar ocorre para baixo em B, devemos realizar o mesmo procedimento do passo 2, mas como o único sinal que vai mudar é o da força F, então, pegando a fórmula:
E trocando o sinal do termo que aparece o (que veio da expressão de ) já resolve nosso problema, então a nova equação se torna:
E, substituindo os valores do enunciado:
Então, deve estar no seguinte intervalo: