Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 36

Localize o centroide do sólido.

Passo 1

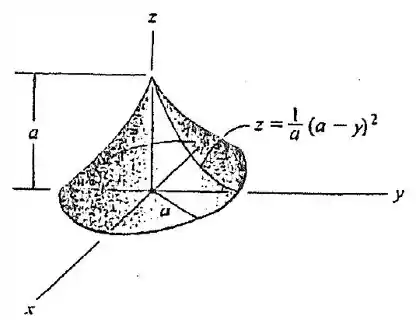
Se liga! Temos um sólido de revolução aí. É como se a gente pegasse essa curva que ele dá e a rodasse em torno de para formar essa área lateral do cone. Por isso, o centro de massa desse cone vai estar sobre o eixo , pela simetria!

Então a primeira coisa que a gente vai fazer é achar um elemento diferencial para a gente montar a fórmulinha do volume e a fórmulinha do centroide. Uma boa ideia, já que nossa sólido tem essa simetria em torno de , seria usar um disquinho bem fino de altura .

Olha essa vista frontal:

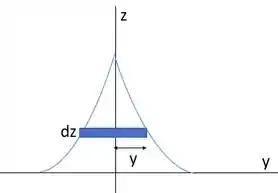
Esses disquinhos são obtidos a partir da base, como se estivéssemos cortando ele de baixo para cima.

Aí a espessura dele fica , e pela figura, o raio de cada disco vai ser . O volume de cada disco fica:

Mas a gente precisa colocar isso em função de , já que estamos usando . A gente pode pegar a equação da curva que o enuciado deu e achar em função de :

Aí nosso volume fica:

Passo 2

Agora a gente usa a fórmulinha de sempre pra achar o centroide!

Esse dentro da integral é distância no eixo da origem até o centroide do disco. Como o centroide do disco é no centro dele que está em no eixo , esse valor dentro da integral vai ser o nosso mesmo.