Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 50
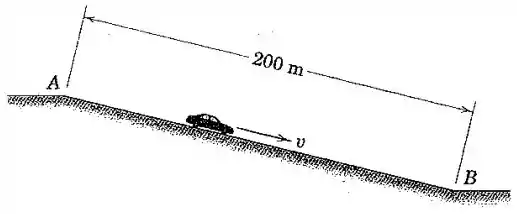
O motorista de um carro, que está inicialmente em repouso no topo de uma ladeira, libera os freios e desce em ponto morto com uma aceleração em metros por segundo ao quadrado dada por , onde é a velocidade em metros por segundo. Determine a velocidade na base da ladeira.
Passo 1
Galera, aqui queremos achar a ao final dos . Como temos a expressão da aceleração em termos da velocidade, e nos foi dada a distância de , temos que usar uma equação diferencial que relacione essas três coisas: velocidade, aceleração e distância.
Então, podemos usar a seguinte equação diferencial:
Substituindo o valor de :
Passo 2
Show! Agora, vamos dar uma ajeitadinha na equação e integrá-la:
Pra calcular a integral da esquerda, lembre-se do seguinte:
Então, temos:
Passo 3
Com a equação que a gente encontrou no passo anterior, vamos tentar isolar , que é o que realmente queremos achar:
Como a aceleração em é , e o carro desce a ladeira sem freios, podemos considerar que a aceleração é sempre positiva, ou seja: