O poste A de aço inoxidável 304 tem diâmetro e está embutido em um tubo de latão vermelho C83400. Ambos estão apoiados sobre a superfície rígida. Se for aplicada uma força de à tampa rígida, determine a tensão normal média desenvolvida no poste e no tubo.

Passo 1
Falaaa meu povo, bora resolver mais essa?
Nós temos esse maravilhoso poste feito de dois materiais, e temos a carga total que o sistema recebe. Cada material vai resistir a uma parcela dessa carga.
Pra determinar a tensão normal em cada material, que é o que ele pede, a gente vai precisar da carga suportada por cada um separadamente. A gente pode desenhar um diagrama de corpo livre pra ver como isso vai rolar.
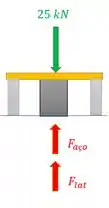
Esse diagrama é tipo um corte do poste, tá? Aí temos a parte de aço que é maciça cilíndrica e a parte de latão que é oca e cilíndrica. Por equilíbrio a gente vê que:
Temos uma equação e duas incógnitas. Então precisamos encontrar mais uma relação entre as duas forças.
Passo 2
Bem, podemos pensar na equação de compatibilidade dos deslocamentos pra resolver essa parada. Como? Vamos analisar como esses caras se deformam por causa da carga. Teriamos algo assim:

A carga age sobre essa “tampa” do poste. Essa tampa não se deforma né? A gente considera pelo enunciado que ela é uma chapa rígida. Então, se não há deformação, ela permance reta. Logo, a altura que ela desce no meio, ela desce igualmente nas extremidades.
Então se o aço encurta um valor , o latão vai ter o mesmo valor de encurtamento, independente da quantidade de carga que cada um recebe. Aí nesse caso:
Lembrando que o deslocamento axial é dado por:
Passo 3
Beleza, sabendo dos nossos objetivos mãos á obra. Vamos usar a equação dos deslocamentos pra encontrar a relação entre as forças:
Pela compatibilidade a gente tem:
Aqui a gente corta o L, e isola o aço.
Pelo nome dos materiais que ele deu, temos esses módulos de elasticidade tabelados:
A área do aço é:
E a área do latão que é um tubo vazado é:
Colocando na equação a gente tem:
Passo 4
Voltando a equação do inicio a gente pode substituir o que encontramos no passo 3.
E isolando:
Então substituindo para a força do aço:
Passo 5
Agora, basta substituirmos os dados na equação da tensão normal:
E com as áreas e forças calculadas temos.
Para o latão, temos: