Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 22
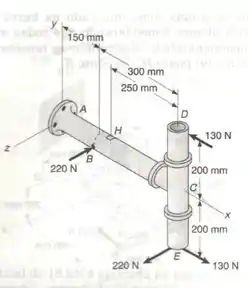
Várias forças são aplicadas à montagem tubular indicada. Sabendo-se que os diâmetros, interno e externo, do tubo são iguais a , respectivamente, determinar:
- Os planos e as tensões principais no ponto localizada no cume da superfície externa do tubo;
- A máxima tensão de cisalhamento no mesmo ponto.
Passo 1
Temos dois objetivos, primeiro precisamos determinar o estado plano de tensões que age no elemento no ponto H, e em seguida precisamos determinar a máxima tensão cisalhante que age nele, para isso precisamos fazer o seguinte:
- Levar todas as forças com seus respectivos momentos fletores até o ponto H
- Com todas as ações no ponto H descartar a parte da seção onde as forças estavam
- Construir o estado plano de tensões no ponto H
- Calcular a máxima tensão cisalhante.
Sabendo isso vamos ao nosso primeiro passo:
Passo 2
Vamos levar as forças até o ponto H com as suas respectivas ações ligadas, se fizermos um elemento unifilar do tubo teremos que:
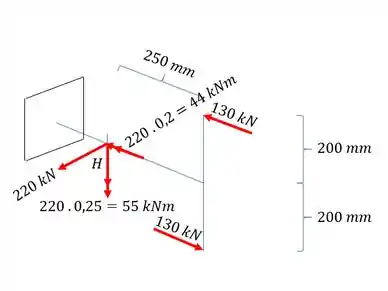
Levando a carga de , teremos que:
E levando a carga de teremos que:
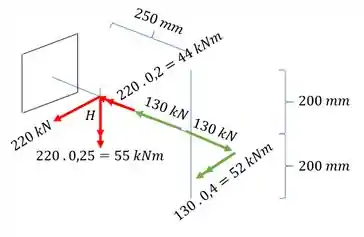
Perceba que as cargas de , se anulam, sendo assim teremos que, juntando os mesmos esforços que estão na mesma direção e descartando todo o resto da estrutura que não afeta mais o ponto H, teremos que:
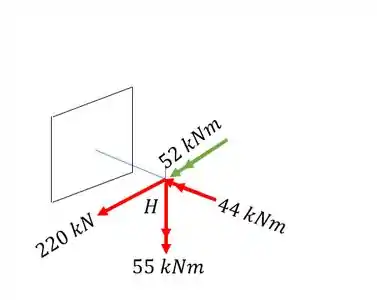
Agora que temos as ações que agem na estrutura, podemos para de olhar a seção como unifilar e podemos olhar ela como uma seção circular, sendo assim teremos que:
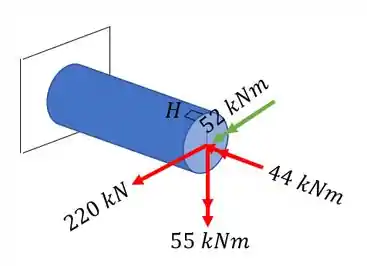
Agora vamos analisar o que cada esforço irá produzir na nossa seção H:
- Sabemos que o momento de 44 kNm tem a tendência de cisalhar a seção com o ponto H.
- Sabemos que o momento de 52 kNm tende a comprimir o ponto H
- A força de 220 kN, também tende a cisalhar o nosso ponto H.
- E o momento de 55 kNm está agindo na mesma seção do ponto H, e sabemos que a tensão na linha de atuação do momento é zero, ou seja, esse esforço não produz nenhuma tensão no nosso ponto H. O que isso significa? Significa que podemos descartar completamente esse esforço porque ele não afetará o ponto H:
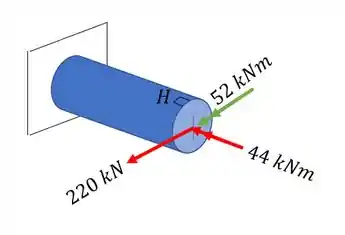
Passo 3
Se já temos os esforços, podemos calcular as tensões que cada um deles produz:
Vamos começar pelas tensões normais:
- Devido ao momento torsor
- Devido ao cortante
Para a tensão normal, é importante lembrar que a fórmula é dada por:
Temos o nosso momento fletor:
A distância em y é o valor do raio externo, que é dado por:
E o momento de inercia da seção vazada é dada por:
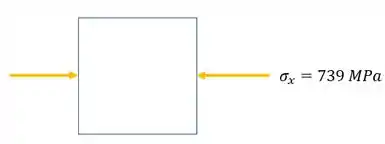
Ou seja, esse esforço, no nosso elementinho, no ponto H, gera uma compressão na direção X, que podemos descrever como:
Passo 4
Se já temos os esforços, podemos calcular as tensões que cada um deles produz:
Vamos para a tensão cisalhante:
Para a tensão cisalhante devido ao momento torsor, é importante lembrar que a fórmula é dada por:
Temos o nosso momento fletor:
é o raio externo do nosso tubo:
E o momento de inercia da seção vazada é dada por:
Ou seja, esse esforço, no nosso elementinho, no ponto H, gera uma tensão cisalhante no nosso ponto H
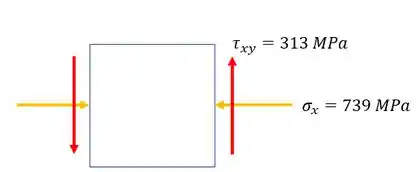
Para a tensão cisalhante devido ao cortante, é importante lembrar que a fórmula é dada por:
Temos o nosso cortante:
é duas vezes a espessura do tubo:
E o momento de inercia da seção vazada é dada por:
E para o momento estático precisamos da seguinte equação:
Como precisamos do momento de inercia da espessura, podemos fazer o seguinte:
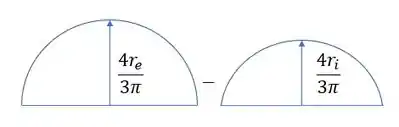
Assim o nosso momento estático será dado por:
Ou seja, esse esforço, no nosso elementinho, no ponto H, gera uma tensão cisalhante no nosso ponto H contrária ao que definimos, sendo assim teremos que:
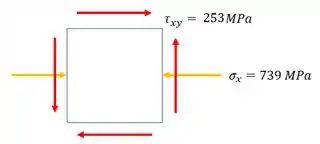
Sendo assim, se subtrairmos as tensões cisalhantes, o nosso elemento passara a ser o seguinte:
E assim fechamos o primeiro objetivo, mas o segundo objetivo é bem simples, que é determinar a máxima tensão cisalhante para este estado plano de tensões, nesse caos precisamos apenas fazer o seguinte:
