Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 1

Se a viga for submetida a um cisalhamento de V = 15 kN, determine a tensão de cisalhamento na alma em A e B. Indique as componentes da tensão de cisalhamento sobre um elemento de volume localizado nesses pontos. Considere w = 125 mm. Mostre que o eixo neutro está localizado em y’ = 0,1747 m em relação à parte inferior e I N A = 0,2182( 10 - 3 ) m 4 .

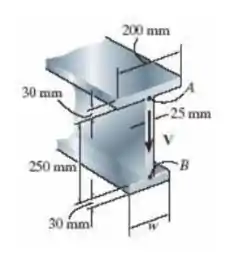
Passo 1

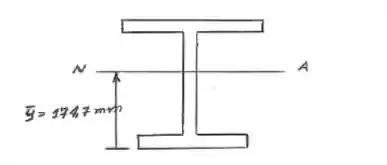
Demonstrar que a posição da linha neutra (ou eixo neutro) é essa mesmo

y C G t o t a l = ∑ A y C G ∑ A = 125 × 30 15 + 200 × 30 295 + 250 × 25 155 125 × 30 + 200 × 30 + 250 × 25 = 174,7   ( C e n t r o i d e   d a   s e ç ã o   t r a n s v e r s a l )

Onde y C G   é a distância do centroide das subdivisões da peça (formada por 3 retângulos) até a base.

Passo 2

Demonstrar o valor de I N A   , o momento de inércia da peça.

I N A = 0,125 × 0,03 3 12 + 0,125 × 0,03 × 0,1597 2 + 0,025 × 0,025 3 12 + 0,025 × 0,025 × 0,0197 2 + 0,2 × 0,03 3 12 + 0,2 × 0,03 × 0,1203 2

Onde cada fator entre colchetes é a contribuição ao momento de inércia de cada subdivisão (3 retângulos)

I N A = 2,1818 × 10 - 4 m 4

Passo 3

Podemos agora obter o momento estático em cada ponto:

Q A = A ' y ' C G = 0,2 × 0,03 0,31 - 0,1747 - 0,015 = 7,218 × 10 - 4 m 3

Q B = A ' y ' C G = 0,125 × 0,03 0,1747 - 0,015 = 5,9888 × 10 - 4 m 3

Passo 4

Agora obtemos a tensão cisalhante em cada ponto por:

τ A = 1,99 M P a

τ B = 1,65 M P a

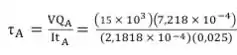
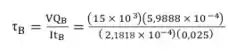
Passo 5

Desenhar o elemento infinitesimal:

Resposta

τ A = 1,99 M P a

τ B = 1,65 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as maiores forças P que o elemento pode suportar se a tensão de cisalhamento admissível for τ a d m = 70M P a . Os apoios em A e B exercem somente reações verticais sobre a viga.
Faça uma representação gráfica da distribuição da tensão de cisalhamento na seção transversal de uma haste com raio c. Quantas vezes a tensão de cisalhamento máxima é maior que a tensão de cisalhament
A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento máxima desenvolvida nas juntas coladas. Os
Determine a tensão de cisalhamento nos pontos B e C localizados na alma da viga de fibra de vidro.
Determine a tensão de cisalhamento máxima que age na seção crítica da viga de fibra de vidro.