Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 111

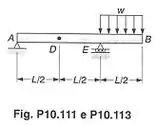
Para a viga prismática mostrada, determinar a deflexão no ponto .

Passo 1

Oi, gente! Tudo bem com vocês? Prontos para essa questão de cálculo de deflexão pelo Teorema de Castigliano?

O enunciado pede para a gente calcular a deflexão no ponto da viga.

Para conseguir fazer esse cálculo, vamos supor que existe uma força fictícia que é aplicada nesse ponto . A imagem abaixo mostra essa situação.

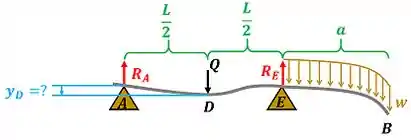
Essa força vale zero, mas precisamos calcular o momento fletor da viga como se de fato existisse. Desse jeito, podemos calcular através da equação 10.77 do livro que calcula deflexões de vigas sobre deflexão.

onde é a derivada parcial do momento fletor em relação à força fictícia!

é a força de reação causada pela restrição no ponto e é a força de reação causada pela restrição no ponto . Precisamos de apenas uma dessas forças para encontrar o momento . No próximo passo, calcularemos .

Passo 2

A primeira etapa para fazer achar é encontrar a reação , fazendo o equilíbrio de momentos em relação ao ponto .

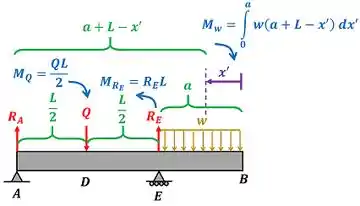
Como a força distribuída e a força fazem a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente dos momentos das forças e .

Agora estamos aptos a achar ! Para achar precisamos usar a equação de equilíbrio de momento na parte direita da barra . Calcularemos o equilíbrio no ponto . O momento tem três valores: um quando a parte direita da barra ainda não inclui a força , o segundo quando a parte direita inclui a força e o terceiro quando a parte direita passa a incluir a força . Vamos começar o cálculo do primeiro valor de .

Colocamos um sinal de menos na frente dos momentos e , porque os dois fazem a viga girar no sentido horário.

Agora vamos calcular o segundo valor de .

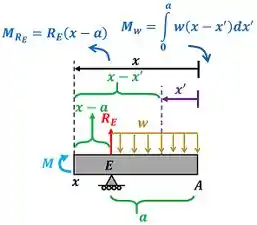
Lembrando que devemos colocar um sinal de menos na frente dos momentos e , porque os dois fazem a viga girar no sentido horário.

Por fim, vamos calcular o terceiro valor de !

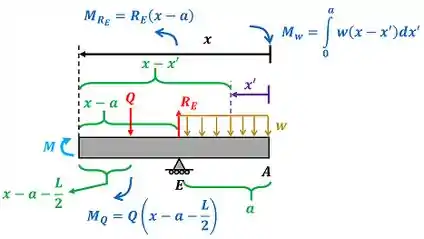
Colocamos um sinal de menos na frente dos momentos , e , porque os três fazem a viga girar no sentido horário.

Com esses três valores de , podemos começar a calcular , determinando os valores de .

Passo 3

Como existem três valores de , existem três valores de . Um para entre e e outro para entre e e um último para de a . Vamos derivar primeiro o primeiro valor de .

Como o termo não possui a variável , essa derivada vale zero.

Agora, vamos encontrar o valor de para o segundo valor de .

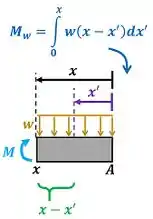
Por fim, vamos encontrar o valor de para o terceiro valor de .

Agora podemos achar .

Passo 4

Como e possuem três valores, precisamos dividir a integral que calcula em três. Uma que vai de a com os primeiros valores de e , outra que vai de a com os segundos valores de e e a última que vai de a com os terceiros valores de e .