Tensão Cisalhante Média e Esforço Cortante
Teoria
Nesse tópico, vamos falar sobre o segundo tipo de tensão, que é a tensão de cisalhamento ou cisalhante.
Introdução
Vamos dizer que você está construindo uma gangorra. Toda gangorra tem uma articulação no meio na forma de um pino:
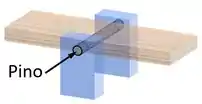
Esse pino está sob a ação de cargas transversais (que agem perpendicularmente ao eixo da peça), como mostra o seu diagrama de corpo livre:
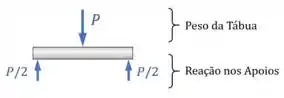
Agora, qual é o valor máximo do peso que podemos fazer nesse pino antes dele quebrar?
Para responder essa pergunta, temos que estudar as tensões no pino. (Lembra? A gente viu que as coisas quebram quando as tensões nela ultrapassam os limites do material.)
Mas não adianta calcular aqui a tensão normal média : As cargas nesse pino não vão gerar uma força normal . Elas vão gerar outro tipo de força interna.
Esforço Cortante e Tensão Cisalhante
Qual é a força interna que vai aparecer nesse pino?
Lembra aí! Tem uma força interna que aparece para equilibrar a peça em situações como essa. É a força cisalhante interna , mais conhecida como força cortante. Agora imagina que o peso da tábua vale , cada reação vai ter e vamos ter isso aqui:
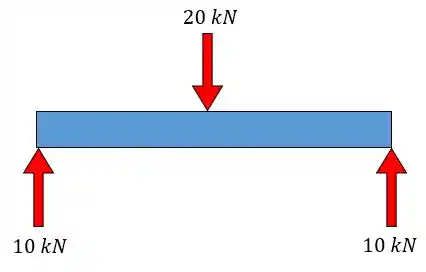
Se a gente fizer uma seção no pino vamos ter o seguinte:
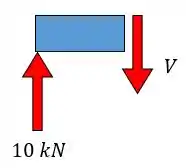
Logo, a cortante vai valer !
Agora vamos pensar...
Se uma força normal gera uma tensão normal, então uma força cortante deve gerar algum outro tipo de tensão.
É aí que entra a tensão cisalhante, representada pela letra grega “tau” ():
- Ela ainda é definida como intensidade de força por unidade de área;
- Mas enquanto a tensão normal só depende das forças normais (perpendiculares) à seção, a cisalhante só depende das forças paralelas;
Podemos representar a tensão normal e a tensão cisalhante no nosso pino:
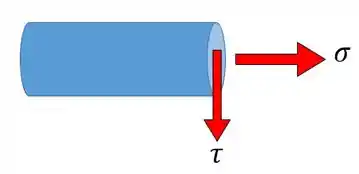
Fórmula da Tensão Cisalhante Média
A tensão normal média em uma seção é calculada dividindo a força normal (que é a resultante de todas as forças normais à seção) pela área da seção.
Sendo a tensão cisalhante aquela que depende das forças paralelas, então a tensão cisalhante média em uma seção é dada por:
onde:
- é a força cortante (que é a resultante de todas as forças paralelas à seção);
- e é a área da seção.
Alguns exercícios vão dizer em qual seção devemos calcular . Nesse caso, devemos:
- Secionar a peça no lugar indicado para encontrar o valor de ;
- Usar quaisquer dimensões fornecidas para calcular ;
- E finalmente aplicar a fórmula .
Mas muitos outros exercícios vão querer que você descubra a “tensão cisalhante na peça”.
Nesses exercícios, devemos buscar analisar a força cortante , a área e a tensão na seção da peça que é mais provável de cisalhar/de se cortar.
Distribuição da Tensão Cisalhante
A distribuição da tensão cisalhante não é uniforme. (Diferentemente da tensão normal que é aproximadamente uniforme.)
Por causa disso, calcular essa tensão cisalhante média só é realmente apropriado para avaliar a resistência de pequenas conexões como: pinos, parafusos e superfícies coladas.
Vou mostrar um exemplo para vocês. Olha essa imagem que mostra a distribuição da tensão cisalhante ao longo de um perfil :
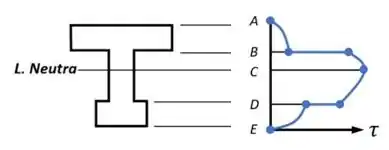
Não dá para rolar uma aproximação né?
Cisalhamento Simples
Existem dois casos de cisalhamento que são muito comuns em conexões e são apelidados de cisalhamento simples e cisalhamento duplo.
Ao reconhecer um desses dois casos, você identifica o valor da força cortante na peça sem ter que fazer uma análise de esforços internos.
Alguns professores não permitem o uso desse “atalho” nas provas, mas muitos permitem e ensinam isso em sala de aula.
Cisalhamento Simples é quando temos apenas uma superfície em contato com outra. Como uma prateleira presa à parede por um parafuso:
Geralmente é feito por parafusos, pinos e pode ser representado da seguinte maneira:
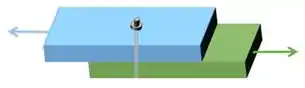
Geralmente ele é representada no 2D na seguinte forma:
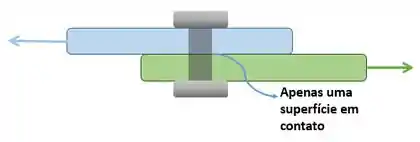
Se você fizer uma análise de esforços internos no parafuso, levando em conta que uma força é aplicada na prateleira:
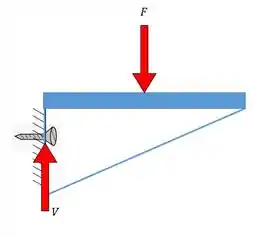
Vai encontrar que:
Ou seja, a força cortante na peça é igual à força transmitida.
Cisalhamento Duplo
É o que acontece quando uma conexão (um pino, um parafuso ) precisa transmitir uma força de uma peça central para duas peças laterais. Algo mais ou menos assim:
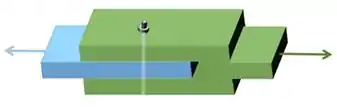
Uma análise de esforços internos nessa conexão revela que:
Faz sentido, né? Teremos duas superfícies de contato, assim, a minha força vai metade pra cada lado do pino ou parafuso. No 2D, isso aí:
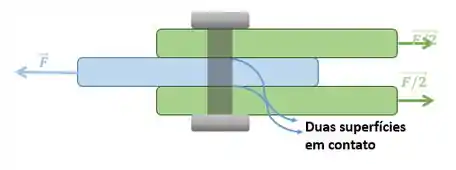
Ou seja, a força cortante na peça é igual à metade da força . (O pino da nossa gangorra é um exemplo de cisalhamento duplo!)
Então se o pino da nossa gangorra tiver uma área de e sofre cisalhamento duplo, qual a tensão cisalhante à qual o pino está submetido? Se esse pino irá romper?
Vamos lá! Olhando o probleminha de novo a gente tem:
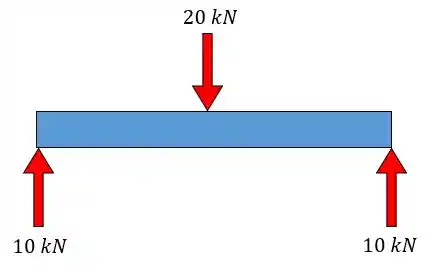
Como vimos o cortante vale , se o problema deu a área então podemos calcular a tensão cisalhante para cisalhamento duplo:
Mas é cisalhamento duplo! Então a força cortante de tem que ser dividida por 2 obtendo:
Agora podemos substituir:
Essa é a tensão de cisalhamento a qual o pino está submetido. Como o pino suporta uma tensão máxima de então não haverá rompimento.
Vale observar que se fosse cisalhamento simples a tensão seria de , ou seja, nesse caso haveria rompimento!
Show de bola? Vamos praticar então!
Fórmula da Tensão Cisalhante Média
Distribuição da Tensão Cisalhante
Cisalhamento Simples
Cisalhamento Duplo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria.
O Dexter, mascote do Responde Aí, gosta de estudar resistência dos materiais enquanto pula de galho em galho na floresta.
Na figura abaixo, ele está se apoiando em um galho que possui uma seção transversal com área . Sabendo que o Dexter gera uma força cortante interna no galho, calcule a tensão cisalhante média nesse galho.
Forneça o resultado em .
Passo 1
O exercício quer saber a tensão de cisalhamento média no galho, então vamos nos lembrar de sua fórmula:
Já temos os valores da força cortante interna no galho e da área da seção transversal do galho:
Então só precisamos aplicar a fórmula da tensão cisalhante média e prestar atenção nas unidades.
Passo 2
Aplicando a fórmula da tensão cisalhante média :
Substituindo os valores de e :
Agora precisamos converter as unidades para .
Vamos pensar... Podemos substituir por . E como um centímetro é , podemos substituir por :
Fazendo a multiplicação e substituindo por , chegamos à resposta:
Resposta
Exercício Resolvido #2
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 40-1.16.
Quando a força alcançou , o corpo de prova de madeira mostrado na figura falhou sobre cisalhamento ao longo da superfície indicada pela linha tracejada. Determine a tensão de cisalhamento média ao longo daquela superfície no instante da falha.
Passo 1
O exercício quer saber a tensão de cisalhamento média na superfície indicada pela linha tracejada, que é a superfície que estava resistindo ao cisalhamento antes da peça falhar.
Para encontrar a tensão de cisalhamento média, vamos nos lembrar de sua fórmula:
Da fórmula, temos que para encontrar o valor de na superfície indicada no instante da falha, devemos encontrar primeiro:
- A força cortante interna resultante nessa superfície no instante da falha;
- A área dessa superfície.
O esforço interno no instante da falha é igual à força , como mostra o Diagrama de Corpo Livre e a análise das condições de equilíbrio na imagem abaixo:
Já a área é retangular e pode ser calculada a partir da espessura do bloco de madeira e do comprimento da superfície.
Passo 2
Começando pelo cálculo da área retangular que se encontrava sob cisalhamento até a peça falhar:
Passo 3
Como já identificamos o esforço interno e a área , podemos substituir esses valores na fórmula da tensão cisalhante média:
Para que tenhamos um resultado em , podemos reescrever a força de como :
Resposta
Exercício Resolvido #3
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 20-1.
Uma placa é fixada a uma base de madeira por meio de três parafusos de diâmetro , conforme mostra a figura. Calcular a tensão média de cisalhamento nos parafusos para uma carga .
Passo 1
Temos uma situação de cisalhamento simples, em que três parafusos iguais de diâmetro estão resistindo juntos à carga .
O exercício pede a tensão de cisalhamento média nos parafusos. que deve ser encontrada pela sua fórmula:
Nos resta encontrar então a força cisalhante interna e a área da seção resistente à essa força .
Passo 2
Podemos interpretar como o esforço interno total, acumulado entre os três parafusos, e como a seção resistente total, acumulada entre os três parafusos.
Se é o esforço interno total, acumulado entre os três parafusos, ele deve resistir à toda a carga , de tal forma que:
E quanto à área ?
Bom, a área da seção transversal de um parafuso de diâmetro é dada pela área de um círculo: .
Então área da seção resistente total, acumulada entre os três parafusos, será 3 vezes isso:
Substituindo :
Passo 3
Agora, podemos inserir os valores que encontramos para e na equação da tensão cisalhante média:
Para conseguir um resultado em , reescrevemos como :
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 26-1.35.
O arganéu da âncora suporta uma força de cabo de . Se o pino tiver diâmetro de , determine a tensão média de cisalhamento no pino.
Passo 1
Nesse exercício, o pino está sob a situação que chamamos de cisalhamento duplo.
Ele transmite entre as peças uma força total , mas a força cortante interna máxima a qual ele está submetido é metade dessa força:
Com esse valor de e com a área da seção transversal do pino (calculada a partir do diâmetro ), conseguimos encontrar a tensão cisalhante média no pino:
E assim o exercício está resolvido.
Se for preciso, Diagramas de Corpo Livre do pino podem ser feitos para provar que :
Do ponto A até o ponto B, temos F/2 para cima. Do ponto B até o ponto C, temos F/2 para baixo.
Passo 2
Vamos começar calculando a área da seção transversal do pino.
É uma área circular e nos foi fornecido o diâmetro dela, então usamos a equação:
Substituindo :
Passo 3
Como já temos e , podemos aplicar a fórmula da tensão cisalhante média:
Para ter resultados em , reescrevemos a força de como :
Resposta
Exercício Resolvido #5
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 40-1.15.
As componentes de madeira e devem ser unidas por cobrejuntas de madeira compensada que serão totalmente coladas às superfícies em contato. Como parte do projeto da junção, e sabendo que a folga entre as extremidades das componentes deve ser , determine o comprimento mínimo permitido para que a tensão de cisalhamento média na cola não exceda .
Passo 1
As madeiras tentam cisalhar (cortar) a cola, gerando uma uma força cisalhante interna na cola, e, consequentemente, uma tensão de cisalhamento média nela.
Quando excede , a cola falha e as madeiras se soltam.
Como reação ao esforço interno que as madeiras geram na cola, a cola faz forças de mesma intensidade nas madeiras. São essas forças que mantêm as madeiras juntas e em equilíbrio:
Como sempre, é a seção resistente à força cisalhante.
Pensa aí! A seção da cola resistente à essas forças é a área retangular na junção entre duas madeiras.
Essa área retangular possui base e altura , como mostram a figura original do exercício e a figura acima, respectivamente.
Para resolver o exercício vamos ter que:
- Calcular a força cisalhante interna na cola;
- Calcular a área da cola resistente à essa força . Essa área vai ser encontrada em função de para evitar muitos cálculos;
- Inserir esses valores na fórmula de tensão cisalhante média e aplicar a condição para encontrar o valor mínimo que deve ter;
- Usar a relação (retirada da figura acima) para finalmente encontrar o valor mínimo que deve ter.
Passo 2
Para calcular a força cisalhante interna , vamos observar o equilíbrio de uma madeira:
Todas as forças estão na vertical, então só precisamos fazer o equilíbrio de forças na vertical:
Como a força de aponta para cima e as forças apontam para baixo:
Vamos guardar esse valor!
Passo 3
Próximo passo é calcular a área da seção resistente de cola ao esforço interno .
Como a área é retangular:
Substituindo :
Passo 4
e calculados, hora da fórmula da tensão cisalhante média
Substituindo os valores encontrados para e :
Lembra aí! Queremos saber qual o valor mínimo de tal que . Então vamos aplicar essa condição:
Isolando :
Passo 5
Pausa para observar as unidades dessa última equação:
(Se quiser, pode fazer essa pausa em uma folha de rascunho!)
Lembra aí! Pascal () é o mesmo que newtons por metro quadrado ().
Então podemos substituir por :
Cortando com :
Arrumando as unidades:
Substituindo por :
Passo 6
Voltando para a nossa equação:
Como :
Calculando:
Ou seja, o valor mínimo de é .
Passo 7
Agora só falta aplicar a relação , como mostra a figura:
Aplicando essa relação e substituindo o valor mínimo de (), encontramos o valor mínimo de :
Resposta
Exercício Resolvido #6
James M. Gere, Mecânica dos materiais, 5ª ed. São Paulo: Pioneira Thomson Learning, 2003, pp. 41-1.6-6-(b).
Um parafuso para finalidades especiais de diâmetro passa através de um furo em uma placa de aço (veja a figura). A cabeça hexagonal do parafuso está direcionada contra a placa de aço. O raio do círculo circunscrito pelo hexágono é (o que significa que cada lado do hexágono tem comprimento ). A espessura da cabeça do parafuso é de e a força de tração no parafuso é de .
Determine a tensão de cisalhamento média na cabeça do parafuso.
Passo 1
O exercício quer saber a tensão de cisalhamento média na cabeça do parafuso:
Precisamos então identificar:
- qual à a força cisalhante interna na cabeça do parafuso;
- e qual é a área da seção resistente à essa força.
Para tanto, vamos visualizar um diagrama de corpo livre da cabeça de um parafuso que está sendo tracionado por uma força :
O que está acontecendo: a placa de aço exerce uma força em volta de toda a cabeça do parafuso, de intensidade total , para o segurar o parafuso no seu lugar.
A linha tracejada indica uma superfície cilíndrica de diâmetro e altura que é a seção resistente ao cisalhamento:
A figura abaixo mostra os esforços internos nessa seção:
Na prática, você não precisa fazer todos esses desenhos. O que precisamos é saber interpretar o exercício para chegar às conclusões que:
- Para garantir o equilíbrio desse pedaço da cabeça do parafuso mostrado na última imagem, deve ser igual à ;
- A área da seção resistente é como a área da face lateral de um cilindro de diâmetro e altura .
A dimensão fornecida pelo enunciado para os lados da cabeça hexagonal do parafuso não será utilizada pela gente nesse exercício: ela não é necessária para encontrar , ou .
Passo 2
Vamos começar então calculando a área .
Pensa aí... A área da face lateral de um cilindro é como o perímetro da base do cilindro vezes a altura do cilindro.
O perímetro de um círculo é . Se é a altura do cilindro, a área fica assim:
Nós não temos o raio da base do cilíndro, mas temos o diâmetro . Como :
Substituindo os valores de e :
Passo 3
Agora podemos aplicar a fórmula da tensão cisalhante média:
Vimos no passo 1 que deve ser igual à e vimos no passo 2 que , então:
Para termos um resultado em , vamos reescrever como :
Fazendo a divisão, isso dá:
Resposta
Exercício Resolvido #7
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 41-1.17.
Duas pranchas de madeira, cada uma com de espessura e de largura são unidas pela junta de encaixe mostrada na figura. Sabendo que a madeira utilizada rompe por cisalhamento ao longo das fibras quando a tensão de cisalhamento média alcança , determine a intensidade da carga axial que romperá a junta.
Passo 1
Existem conexões que estão resistindo ao cisalhamento gerado pela força :
Observando uma dessas conexões de perto, conseguimos identificar uma seção resistente ao cisalhamento, como indicado pela linha tracejada na figura abaixo:
Cada uma dessas seções resistentes possui dimensões de :
- a dimensão de vem da figura original do exercício;
- e a de corresponde à espessura das pranchas de madeira.
Para o equilíbrio da prancha de madeira, cada uma dessas seções deve exercer uma força cisalhante interna de tal forma que a soma de todas as forças seja igual à força :
Entendido o que está acontecendo no exercício, vamos pensar agora em como resolvê-lo:
- O exercício quer saber o valor da força necessária para provocar uma falha nas juntas;
- Para encontrar , precisamos encontrar primeiro o valor da força de cisalhamento interna necessária para romper uma junta;
- pode ser encontrado usando a fórmula da tensão cisalhante média , uma vez que o exercício já nos disse que é necessário uma tensão para romper a madeira;
- Antes de usarmos a equação , só precisamos calcular antes a área da seção de dimensões .
Passo 2
Vamos começar então pelo cálculo das áreas !
Em uma prancha de madeira, existem seções resistentes ao cisalhamento.
Cada uma dessas seções possui dimensões de (comprimento da seção resistente) por (espessura da prancha de madeira).
Então, a área de uma dessas seções é dado por:
Passo 3
A tensão de falha da madeira foi fornecido pelo exercício e agora encontramos a área de uma seção resistente.
Então podemos calcular a força cisalhante interna de falha das juntas através da fórmula da tensão cisalhante média:
Substituindo os valores de e :
Isolando :
Como :
Passo 4
Como a força precisa provocar esforços internos nas juntas de uma prancha de madeira:
Se for necessário, um Diagrama de Corpo Livre e uma análise das condições de equilíbrio podem ser feitas para provar essa relação:
Como :
Reescrevendo em :
Resposta
Exercício Resolvido #8
James M. Gere, Mecânica dos materiais, 5ª ed. São Paulo: Pioneira Thomson Learning, 2003, pp. 41-1.6-4-(b).
A conexão mostrada na figura consiste de cinco placas de aço, cada uma com de espessura, unidas por um único parafuso de de diâmetro. A carga total transferida para as placas é , distribuída entre as placas como mostrado.
Calcule a maior tensão de cisalhamento agindo contra o parafuso.
Passo 1
Nesse exercício várias forças diferentes estão atuando no parafuso, fazendo com que a força cisalhante interna varie ao longo das seções do parafuso.
Precisamos avaliar as diferentes seções do parafuso (entre a 1ª e a 2ª placa, entre a 2ª e a 3ª, etc.) para encontrar o maior esforço interno .
Com isso, poderemos calcular a maior tensão de cisalhamento agindo contra o parafuso.
Vamos fazer uma resolução em partes:
- Fazer um Diagrama de Corpo Livre do parafuso e avaliar as suas seções para encontrar a maior força cisalhante interna, ;
- Calcular a área da seção transversal do parafuso usando o diâmetro ;
- Usar a fórmula da tensão cisalhante média para encontrar a maior tensão cisalhante, .
Passo 2
Começando pelo Diagrama de Corpo Livre:
A partir desse diagrama, conseguimos identificar as diferentes seções transversais do parafuso que podem ter valores distintos de , como feito abaixo com as linhas tracejadas:
Feito o Diagrama de Corpo Livre, o próximo passo é fazer a análise dos esforços internos nas diferentes seções:
Dessa análise, tiramos que a intensidade máxima da força cisalhante interna é igual à intensidade dessa força nas seções e :
Passo 3
Já temos , o que significa que estamos perto de encontrar .
Antes disso, vamos só calcular o valor da área da seção transversal.
A seção transversal do parafuso é circular. Lembra aí... A área do círculo pode ser dada em função do seu diâmetro pela fórmula:
Substituindo :
Passo 4
Usando a força cisalhante interna máxima na equação da tensão cisalhante máxima , encontramos :
Substituindo e :
Como :
E assim obtemos nosso resultado:
Resposta
Exercício Resolvido #9
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 30-1.67.
A viga é apoiada por um pino em e um elo curto . Se , determine a tensão de cisalhamento média desenvolvida nos pinos em , e . Todos os pinos estão sujeitos a cisalhamento duplo, como mostra a figura, e cada um tem diâmetro de .
Passo 1
Fala aí, galerinha! O problema pede para que calculemos as tensões cisalhantes dos pinos e ainda falou que trata-se de cisalhamento duplo. Vamos relembrar aqui que cisalhamento duplo tem a seguinte equação:
Onde é a força cortante.
Show de bola! Mas precisamos entender também que a viga é mantida em equilíbrio pelas reações:
- do apoio (uma reação na vertical, , e uma na horizontal, );
- e da haste (uma força , no sentido da própria haste),
como mostra o seu Diagrama de Corpo Livre:
Passo 2
Aplicando as condições de equilíbrio nessa viga e sabendo que , conseguimos calcular o valor das reações , e .
Vamos começar aplicando as condições de equilíbrio no diagrama de corpo livre da viga:
Lembra aí! As condições de equilíbrio possíveis são equilíbrio de forças (na vertical e na horizontal) e equilíbrio de momentos (em relação à algum ponto).
Como temos incógnitas (, e ), condições de equilíbrio são o suficiente!
Vamos fazer o equilíbrio de momentos em relação ao ponto (vamos fazer isso para poder eliminar a força e ficar mais fácil o cálculo, já que não gera momento em ) e o equilíbrio de forças nas duas direções.
Começando pelo equilíbrio de momentos:
Em relação ao ponto , só as cargas e a força geram momentos e os braços dessas forças podem ser vistos no DCL acima. Além disso, só a força gera um momento no sentido anti-horário.
Tendo tudo isso em mente, o somatório de momentos fica assim:
Somando todas as forças :
Isolando :
Uma incógnita descoberta, faltam duas!
Agora podemos partir para o equilíbrio de forças na vertical:
Tomando o devido cuidado de decompor a força , esse somatório de forças fica assim:
Somando as forças :
Como e :
Isolando :
e descobertas, agora só falta encontrar .
Finalmente, temos o equilíbrio de forças na horizontal:
Mais uma vez tomando o cuidado de decompor , esse somatório de forças fica assim:
Isolando e substituindo :
Como :
Passo 3
Reações descobertas! Antes de calcular as tensões em cada pino, vamos só calcular a área da seção transversal dos pinos.
Por se tratar de uma seção circular de diâmetro :
Passo 4
Agora podemos calcular as tensões em cada pino. Vamos olhar o pino isoladamente para entender o que está acontecendo:
Olha como as duas forças e atuam no plano da seção transversal. Isso faz com que ambas contribuam para a tensão de cisalhamento. Então podemos juntar as duas numa força só
Juntas, as duas reações em formam uma força , que é a força a qual o pino em está sujeito sob cisalhamento duplo.
A tensão cisalhante média nesses pinos é dada pela sua fórmula:
Ou seja, para o pino em vamos ter:
Para todos os pinos, a área da seção transversal é a mesma e vai ser calculada a partir de seu diâmetro .
Para o pino em , precisamos primeiro calcular a força resultante nesse ponto. Como temos duas forças e perpendiculares, usamos o teorema de pitágoras:
Substituindo e :
Aplicando a fórmula da tensão cisalhante média para o pino em , que está sob cisalhamento duplo de tal forma que , temos:
Substituindo , e :
Para obtermos resultados em , podemos reescrever como :
Calculando, isso dá:
Passo 5
Para os pino em e , já temos o valor da força que atua neles. Da mesma forma que o pino a força vai ser a própria força da fórmula:
Pessoal, o pino e o pino têm a mesma força atuando e possuem a mesma área. Logo estão sujeitos à mesma tensão cisalhante .
Aplicando a fórmula da tensão cisalhante média , tendo em mente que esses pinos estão sob cisalhamento duplo de tal forma que , temos:
Substituindo , :
Vemos que essa é a mesma conta de , então já podemos adiantar que:
Resposta
Exercício Resolvido #10
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 30-1.69.
A estrutura está sujeita a carga de . Determine a tensão de cisalhamento média no parafuso em em função do ângulo da barra . Represente essa função em gráfico para e indique os valores de para os quais essa tensão é mínima. O parafuso tem diâmetro de e está sujeito a cisalhamento simples.
Passo 1
A tensão de cisalhamento média no parafuso vai ser dada pela equação de sempre:
A área será encontrada através do diâmetro do parafuso.
Mas e a força cisalhante interna ?
O parafuso está sobre cisalhamento simples, o que significa que a força cisalhante interna no parafuso é igual à força que uma peça da estrutura faz na outra no ponto .
Podemos encontrar o valor de analisando as condições de equilíbrio da peça inferior da estrutura. Para isso, vamos precisar de um DCL (Diagrama de Corpo Livre) dessa peça:
No caso, é o equilíbrio de momentos em relação ao ponto que vai nos permitir relacionar a força com a carga de .
Dessa forma, vamos encontrar o valor de em função do ângulo e, consequentemente, poderemos encontrar a tensão em função do ângulo .
Finalmente, para representar o gráfico de em função de e encontrar os valores de para os quais a tensão é mínima, vamos precisar usar um pouco de cálculo.
Passo 2
Vamos começar então pelo DCL da peça inferior da estrutura:
Vamos lembrar... As condições de equilíbrio que podemos aplicar nesse são:
- equilíbrio de forças (que podem ser horizontais ou verticais);
- e equilíbrio de momentos (que precisa ser em relação a algum ponto).
Nesse caso, não precisamos descobrir o valor das reações horizontal e vertical no apoio em , e . A nossa incógnita de verdade é a força , que queremos encontrar em função do ângulo .
Isso significa que o equilíbrio de momentos em relação ao ponto vai ser o suficiente para as nossas necessidades:
Para fazer esse equilíbrio de momentos, vamos nos lembrar de uma coisa: O momento gerado por uma força é igual à essa força vezes o seu braço .
Calcular o braço de uma força inclinada como é difícil:
Mas fica fácil se a gente decompor em suas componentes horizontal (que vai ter um braço de ) e vertical (que vai ter um braço de ):
Feita a decomposição, agora podemos voltar para o equilíbrio de momentos:
Simplificando essa expressão:
Isolando :
Ainda podemos simplificar essa expressão!
Como todos os números são múltiplos de :
Como :
Passo 3
encontrado, agora vamos encontrar o valor da área .
O pino possui uma seção transversal circular de diâmetro , então podemos usar a formula da área circular em função do diâmetro:
Passo 4
Aplicando a fórmula da tensão cisalhante média:
Substituindo os valores encontrados:
Para ter resultados em , podemos reescrever como :
Passo 5
Precisamos e descobrir para quais valores de a tensão é mínima.
Vamos observar a expressão que encontramos para :
Essa expressão vai ser mínima quando a expressão for máxima.
Mas como vamos conseguir descobrir para que valores de a expressão é máxima?
Se lembrarmos de Cálculo 1, vamos nos lembrar que o máximo e mínimo das funções acontecem quando a sua derivada é igual a zero:
Vamos lembrar mais um pouco de C1!
Derivada de seno é cosseno e derivada de cosseno é menos seno, então essa derivada fica assim:
Agora temos que isolar :
Usando a função ou da sua calculadora:
Ou seja, ou é mínimo ou é máximo quando .
Passo 6
Ainda precisamos descobrir se é máximo ou mínimo quando .
Mas também precisamos esboçar um gráfico da tensão em função de .
Então vamos aproveitar para fazer as duas coisas ao mesmo tempo, calculando o valor de para alguns valores de :
Com esses valores, confirmamos que é mínimo quando e conseguimos fazer o esboço do gráfico de em função de :
