Tensão Normal Média
Teoria
Opa, seja bem vindo ao Responde Aí! Bora bater um papo sobre Tensão Normal?
O que é Tensão Normal?
Antes de te responder isso, eu vou te dar um exemplo…Se lembra daqueles filmes e desenhos americanos em que as crianças tinham casas da árvore?
Eu não se você, mas eu sempre quis ter uma! Então vamos imaginar que esse dia chegou, hoje vamos construir uma casa na árvore!
-Mas per aí, quanto peso a árvore suporta sem quebrar?!
Isso vai depender de diversos fatores, como:
- Intensidade da força de compressão;
- Propriedades mecânicas do tronco;
- Área da seção transversal do tronco.
Esse último tópico tem tudo a ver com o que vamos estudar hoje! Bora entender isso melhor?
Conceito de Tensão Normal
Tensão
Ela é bem comum sim, mas o nome não vem daí! A tensão normal tem esse nome pois ela só depende das forças normais, ou seja…das forças perpendiculares a sua área transversal. Saca só:
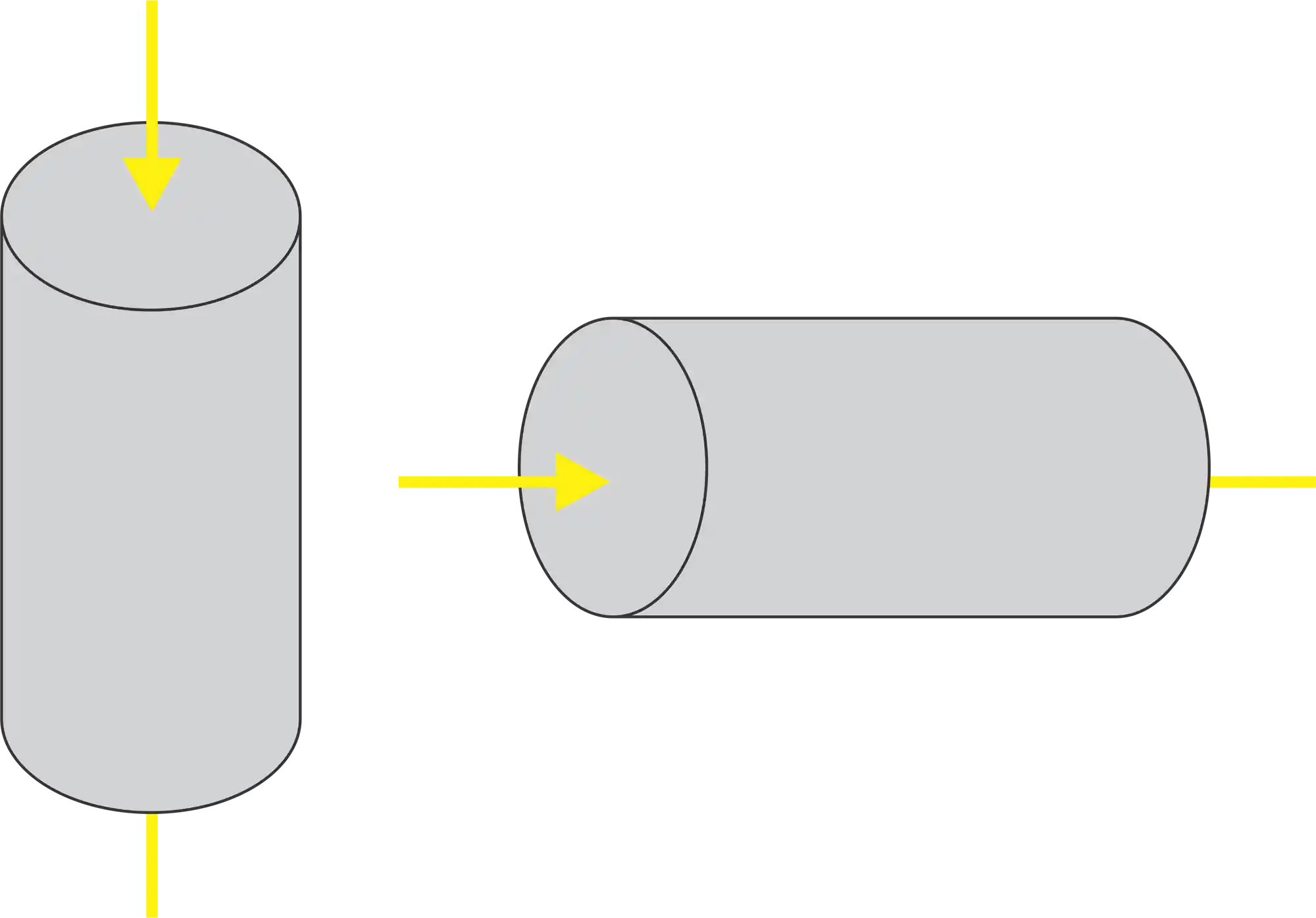
E o que isso te lembra? SIM, o tronco da nossa árvore! 😍 No nosso exemplo terá uma força de compressão, que vem do peso da casinha e das pessoas dentro dela e o solo responde com uma força de mesmo módulo:
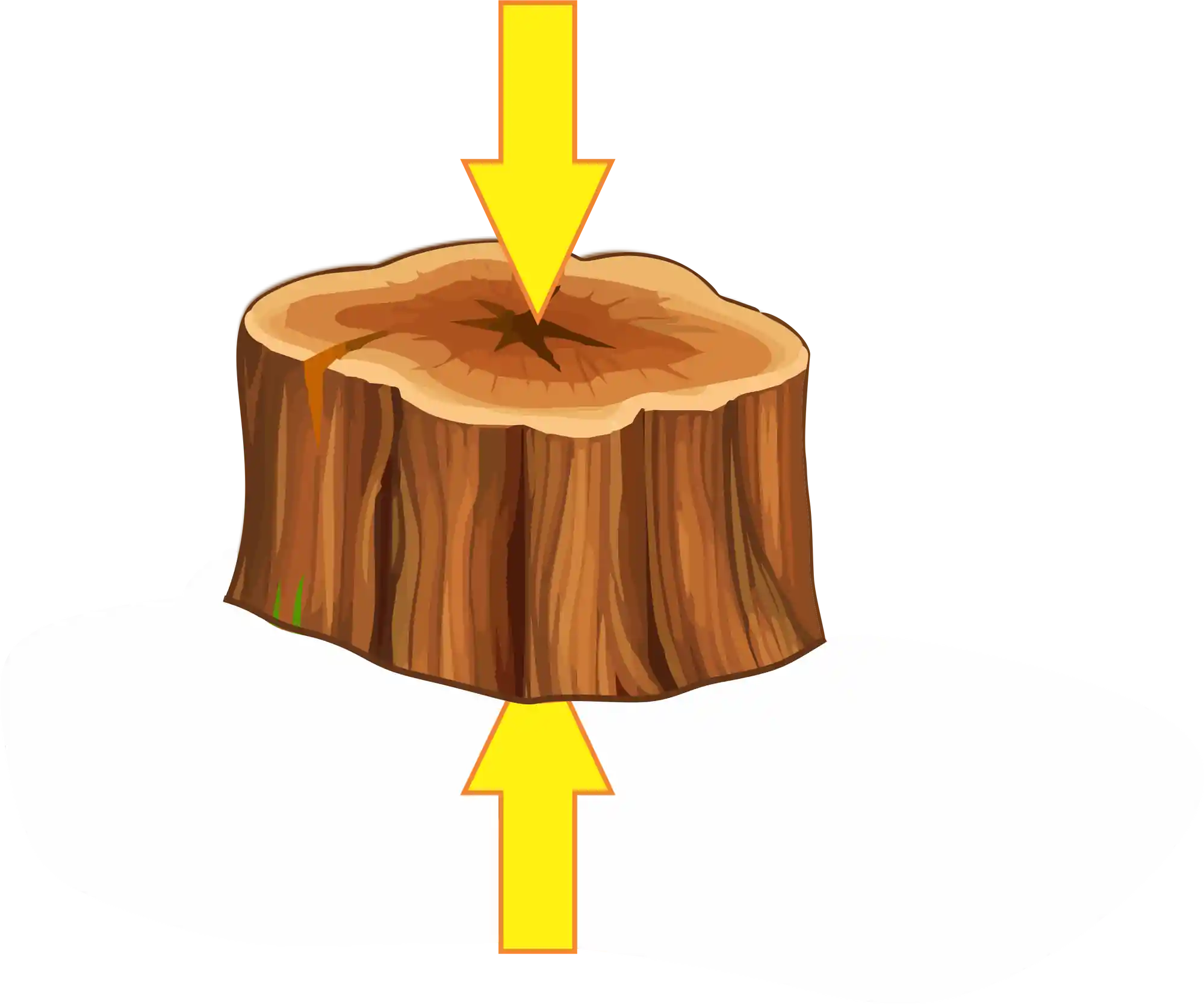
Estamos mais perto de descobrir como faremos pra construir nossa casa na árvore sem riscos de acidentes! ⚠️
Tensão Normal Média: Fórmula
A tensão normal média é dada pela divisão da força normal, que é igual à força aplicada perpendicularmente a sua secção transversal e a área da seção transversal da coluna.
A força normal resultante é calculada por uma análise de esforços internos e a área da seção transversal, calculada a partir de dimensões da peça como o seu diâmetro!
Agora sim, podemos calcular quanto peso a nossa árvore aguenta! 👇
Exemplo: Determine a Tensão Normal
Pra fechar, confere esse exemplo resolvido em vídeo!
Agora vamos praticar com exercícios?
Exemplo: Determine a Tensão Normal
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
O Dexter, mascote do Responde Aí, possui massa de . Ele estava de bobeira por aí quando de repente viu um caixote, também de bobeira. O Dexter, hiperativo, nem pensou duas vezes e pulou em cima do caixote.
A seção transversal do caixote é quadrada e possui de lado, como mostra a figura abaixo:
Qual a tensão normal média, em , exercida pelo Dexter no caixote? Considere .
Passo 1
O peso do Dexter exerce uma força no caixote, que possui um topo quadrado de lado :
Essa força gera um esforço interno normal no caixote. Esse esforço interno gera uma tensão normal média . Precisamos encontrar essa tensão .
Sabemos que , e .
Passo 2
Da fórmula da tensão normal média, temos que:
Como e como a área é uma área quadrada de lado :
Substituindo os valores de , e :
O exercício quer um resultado em , então vamos pensar:
- é um newton ();
- E dá pra reescrever como ,
então isso fica assim:
Calculando a parte de baixo:
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #2
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 21-3.
Determinar a tensão normal de compressão mútua (ou tensões de “contato” ou tensão de “esmagamento”) da figura entre:
- o bloco de madeira de seção e a base de concreto ;
- a base de concreto e o solo.
Passo 1
O exercício quer saber a tensão normal de compressão nos materiais na superfície de contato entre eles.
Em ambos os casos, a força que gera a compressão é a mesma força de .
No item a), a seção de contato é igual a seção do bloco de madeira. Já no item b), a seção de contato é igual a seção da base de concreto.
Passo 2
Já sabendo a força e a área da seção de interesse, é só aplicar a fórmula de tensão normal.
Para o item a), fica assim:
Como, no geral, preferimos resultados em , podemos converter as dimensões da nossa seção de milímetros para metros. Lembrando que , então
Passo 3
Para o item b), já colocando direto as dimensões da seção em metros, da mesma forma que fizemos antes, a fórmula da tensão normal fica assim:
Resposta
- .
- .
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 25-1.34.
A coluna está sujeita a uma força axial de aplicada no centroide da área da seção transversal. Determine a tensão normal média que age na seção . Mostre como fica essa distribuição de tensão sobre a seção transversal da área.
Passo 1
A tensão normal média , pedida pelo exercício, é dada pela divisão da força normal interna (que é igual à força aplicada de ) e a área da seção transversal da coluna.
Para calcular a área , devemos observar sua geometria:
Da imagem, vemos que a área é composta por duas áreas “vermelhas” de largura e comprimento , e uma área “azul” de largura e comprimento .
Sendo assim:
Usando a fórmula da tensão normal média:
Como :
Resposta
A distribuição de tensão sobre a seção transversal é uniforme:
Exercício Resolvido #4
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 38-1.5.
Um medidor de deformação localizado em na superfície do osso indica que a tensão normal média no osso é , quando o osso está submetido a duas forças de como mostra a figura.
Supondo que a seção transversal do osso em seja anular e sabendo que seu diâmetro externo é , determine o diâmetro interno da seção transversal do osso em .
Passo 1
As duas forças de geram esforços internos dentro do osso. Podemos fazer uma seção em e ver como, para garantir o equilíbrio, o esforço interno normal é igual a .
Esse esforço interno gera uma tensão normal média na seção transversal , que possui um formato de anel, como mostra a figura abaixo:
O exercício nos pede para descobrir o valor do diâmetro interno .
Precisamos primeiro encontrar qual é a área que a seção transversal deve ter, e, em seguida, relacionar essa área com .
Passo 2
Para que o esforço interno gere uma tensão , a seção transversal deve ter uma determinada área , como mostra a fórmula da tensão normal média:
Isolando a área :
Como :
Vamos guardar esse resultado!
Passo 3
A área da seção transversal é igual a área do círculo maior menos a área do círculo menor.
Mas lembra aí, a área do círculo é , onde é o raio do círculo. Como o raio é metade do diâmetro, podemos reescrever essa área do círculo como , ou, melhor ainda, !
Assim conseguimos calcular as áreas dos círculos maior e menor, e, consequentemente, calcular a área da seção, que é a diferença entre as áreas do círculo:
Queremos encontrar , então vamos isolá-lo!
Substituindo o valor fornecido de e o valor encontrado para a área :
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 27-1.40.
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir , determine a maior carga vertical aplicada no centro que ele pode suportar.
Passo 1
Para que o material não falhe, é necessário que a tensão normal média seja menor que o seu valor máximo admissível :
Como e o esforço interno normal é igual a carga vertical externa :
O valor máximo de ocorre quando essa expressão é uma expressão de igualdade:
Precisamos calcular o valor da área da seção transversal do bloco para poder encontrar . Para tanto devemos observar a geometria da seção:
Passo 2
Primeiro, calculamos a área .
Na imagem acima vemos como a área da seção transversal do bloco pode ser dividida em áreas menores que se repetem.
Temos duas faixas longas iguais (pintadas de vermelho na imagem) e três “pontes” iguais (pintadas de azul).
Aproveitando essa simplificação, o cálculo da área fica assim:
Passo 3
Agora que temos a área, podemos voltar para a expressão que havíamos encontrado anteriormente:
Substituindo os valores de e :
Se lembrarmos que , podemos simplificar as unidades:
Resposta
Exercício Resolvido #6
Ferdinand P. Beer, E. Russel Johnston, Jr., John T. DeWolf, Resistência dos materiais: mecânica dos materiais, 4ª ed. Porto Alegre: AMGH, 2010, pp. 17-1.1.
Duas barras circulares maciças são soldadas no ponto , como mostra a figura. Determine a tensão normal no ponto médio de cada barra.
Passo 1
Se a gente se lembrar da fórmula da tensão normal (), vamos ver como, para determinar as tensões normais médias de cada barra, precisamos saber:
- a força interna normal em cada barra;
- e a área da seção transversal de cada barra.
Então vamos pensar!
Quanto às forças internas: A barra está sobre ação somente da força de , então . Já a barra está sobre ação das forças de e , ou seja, .
E quanto às áreas das seções? Os diâmetros e podem ser usados para encontrar as áreas e .
Passo 2
Para a barra :
Para a área, vamos nos lembrar de que a área do círculo em função do seu diâmetro é :
Substituindo e :
Resultados assim em (também conhecido como ) não são muito comuns. Para resolver isso, podemos reescrever a força de como . Aí o resultado sai em (ou ):
Calculando tudo, isso dá:
Passo 3
Para a barra :
Mais uma vez, vamos escrever:
- a força interna em newtons (para que o nosso resultado saia em );
- a área do círculo em função do seu diâmetro ().
Com isso, a equação anterior fica assim:
Como :
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #7
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 26-1.37.
O mancal de encosto está sujeito às cargas mostradas. Determine a tensão normal média desenvolvida nas seções transversais que passam pelos pontos , e .
Passo 1
Para calcular as tensões normais médias , precisamos encontrar o módulo das forças normais internas e o valor das áreas de cada seção transversal.
As áreas podem ser encontradas a partir dos diâmetros fornecidos , e .
Para encontrar as forças internas, vamos precisar nos lembrar da matéria de esforços internos: vamos ter que realizar seções em , e , fazer o diagrama de corpo livre (“DCL”) dessas seções e avaliar as condições de equilíbrio.
Passo 2
Vamos começar calculando as áreas de cada seção!
As 3 seções transversais são circulares e nos foi fornecido os seus diâmetros , então podemos usar a fórmula de área do círculo .
Para a seção , temos:
Para a seção :
E finalmente para :
Passo 3
Agora vamos ter que calcular as forças internas em cada uma das 3 seções: , e .
Nesse exercício, só importa para a gente a intensidade da força interna (não precisamos nos preocupar com a direção ou sinal dessa força.)
Isso significa que podemos fazer uma análise um pouco mais “nas coxas”:
- Para cada seção, escolhemos entre fazer o DCL da parte da peça superior à seção (como foi feito com as seções e na imagem abaixo) ou fazer o DCL da parte inferior à seção (como feito para a seção ).
- Em cada DCL, desenhamos as forças externas (em azul na imagem) atuantes nessa parte da peça. Depois desenhamos forças internas (em vermelho) de forma a balancear as forças externas e destacamos os valores encontrados para elas.
Na prática, essa análise fica assim:
Passo 4
Agora temos tudo em mãos para calcular as tensões com a fórmula .
Para a seção , e :
Para , e :
E finalmente, para , e :
Resposta
Exercício Resolvido #8
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 38-1.1.
Duas barras cilíndricas de seção transversal cheia e são soldadas uma à outra em e submetidas a um carregamento conforme a figura. Determine a intensidade da força para a qual a tensão normal de tração na barra é duas vezes a intensidade da tensão de compressão da barra .
Passo 1
O exercício quer descobrir para que valor da força a relação a seguir é satisfeita:
Para calcular as tensões normais e , utilizaremos os seguintes dados:
- , uma vez que a barra está submetida somente à força de tração ;
- , uma vez que a barra está majoritariamente sobre compressão por parte das duas forças de , mas ainda está submetido também à força de tração ;
- , .
Como e estão em função de , as duas tensões, e , também vão ficar em função de .
Isso significa que quando usarmos a relação , vamos ter que manipular a expressão para isolar a força e descobrir o valor que ela deve ter.
Passo 2
A primeira coisa a fazer nesse exercício é calcular as tensões em e usando a fórmula da tensão normal média.
Para a barra , fica assim:
Já sabemos que .
Quanto à área , as barras possuem seção transversal circular, então podemos encontrar as áreas através da expressão . Como :
Não vamos simplificar mais essa expressão no momento pois essa tensão vai ser relacionada depois com a tensão , que também vai ter os termos “”, “” e “” na mesma posição.
Ou seja, vamos poder cortar esses termos com facilidade depois, como mostra a imagem abaixo:
Para a barra , como e :
Passo 3
Agora, aplicamos a relação :
Simplificando:
Isolando :
Calculando, isso dá:
Resposta
Exercício Resolvido #9
Lista de Exercício - Prof. Willian - Universidade Catolica Dom Bosco - Exercicio 1.36.
A luminária de é suportada por duas hastes de aço acopladas por um anel em . Determinar qual das hastes está sujeita à maior tensão normal média e calcular seu valor. Sabemos que . O diâmetro de cada haste é dado na figura.
Passo 1
Para descobrir qual haste está sujeita à maior tensão normal média, vamos precisar calcular a tensão em cada haste.
Então, para calcular essas tensões , vamos precisar da força interna em cada haste e da área da seção transversal de cada haste.
As hastes estão sendo tracionadas para suportar o peso da luminária . Se fizermos um equilíbrio de forças no ponto , vamos descobrir o valor das forças de tração nas hastes:
Como as hastes só sofrem essas forças de tração, podemos garantir que as forças internas serão iguais a essas forças de tração. Daí encontramos que e .
Já para encontrar as áreas e , vamos ter que usar os diâmetros fornecidos: e .
Passo 2
Para encontrar as forças de tração e consequentemente as forças internas , vamos voltar para o diagrama de forças no ponto :
Lembra aí, o equilíbrio de forças acontece quando o somatório de forças é igual a zero ().
Um jeito de ver isso é vendo se a soma das forças na vertical dá zero () e se a soma das forças na horizontal dá zero ().
Para fazer essas somas, vamos ter que decompor as trações em suas componentes verticais e horizontais.
Isso significa ter que usar seno e cosseno para encontrar essas componentes, como mostra a imagem abaixo:
Passo 3
Com a decomposição das forças já feita, agora podemos fazer os equilíbrios de forças na vertical e na horizontal!
Equilíbrio de forças na vertical:
Como na vertical temos as componentes verticais de e apontando para cima e a força peso apontando para baixo, essa expressão acima fica assim:
Como encontramos na decomposição das trações que e :
Vamos guardar essa equação por enquanto!
Em seguida vem o equilíbrio de forças na horizontal:
Como na horizontal temos a componente horizontal de apontando para a direita e a componente horizontal de apontando para a esquerda:
Substituindo os valores e encontrados na decomposição de forças
Vamos também guardar essa equação!
Passo 4
As duas equações que guardamos no passo anterior compõem um sistema de equações:
Se resolvermos esse sistema, encontraremos e (e consequentemente e !)
Bora resolver!
Da segunda equação, encontramos que:
Substituindo esse valor de na primeira equação:
Como :
Substituindo esse valor na segunda equação do sistema:
Pronto! Agora podemos dizer que encontramos e !
Passo 5
Calculando as áreas das seções transversais das hastes com a fórmula :
Como :
E como :
Passo 6
Temos as forças internas e as áreas ! Hora de calcular as tensões:
Substituindo os valores encontrados nos últimos dois passos:
Passo 7
Calculadas as tensões, vemos como a maior tensão é , mas, antes de anunciar o resultado do problema, temos mais uma coisa para observar!
Existe uma unidade utilizada para pressão e tensão chamada . O nome dessa unidade vem do inglês pounds(-force) per square inch.
Traduzindo para o português, fica libras-força por polegadas ao quadrado, que é exatamente o que temos no nosso resultado.
Isso significa que podemos reescrever nosso resultado assim:
Resposta
Exercício Resolvido #10
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 39-1.8.
Sabendo que a porção central da barra tem uma área de seção transversal uniforme de , determine a intensidade da carga para qual a tensão normal naquela parte de é .
Passo 1
Inicialmente, vamos ignorar o desenho e começar prestando atenção no enunciado do exercício.
A barra possui uma tensão normal média e uma área de seção transversal .
Com essas informações, nós podemos aplicar a equação da tensão normal média () na barra para encontrar a força normal interna :
Só tem um problema, o exercício não quer saber o valor da força na situação em que , ele quer saber o valor da força nessa situação.
Então vamos observar o desenho: como é que a força se relaciona com o que está ocorrendo na barra ?
A barra está apoiando a barra curva , contribuindo de alguma forma para o seu equilíbrio.
Esse apoio se dá através de uma força de apoio que pode estar na direção da barra ou em outra direção, como mostra a imagem:
Como a barra deve se manter em equilíbrio, concluímos que está na direção da barra.
Por outro lado, como a barra curva deve se manter em equilíbrio, a força deve gerar, em relação ao ponto , um momento contrário ao momento gerado pela força .
Esse equilíbrio de momentos vai relacionar e .
Mas espera aí, a força , desse jeito, na direção da barra , realizando compressão, gera uma força interna normal de mesma intensidade:
Então o equilíbrio de momentos vai nos permitir relacionar e .
E nós já vamos ter descoberto usando a equação da tensão normal média e assim vamos resolver o exercício!
Passo 2
Vamos começar calculando a força interna a partir da equação da tensão normal média:
Como e :
Lembrando que , chegamos ao resultado:
Passo 3
O próximo passo é relacionar e através do equilíbrio de momentos da barra curva .
Para fazer isso, vamos desenhar o Diagrama de Corpo Livre de :
Para fazer o equilíbrio de momentos em relação ao ponto , vamos querer decompor a força em suas componentes vertical e horizontal, para que os seus braços sejam fáceis de calcular.
Para facilitar o cálculo do braço da força , já vamos também deixar calculado a distância entre as linhas horizontais que passam pelos pontos e .
Com essas duas mudanças, o diagrama de corpo livre de fica assim:
Realizando o equilíbrio de momentos em relação ao ponto :
Substituindo e :
A única coisa que nos falta agora é encontrar os valores de e .
Passo 4
O ângulo é o ângulo que a força faz em relação à horizontal, e, consequentemente, é o ângulo que a barra faz em relação a horizontal:
Dessa imagem, podemos calcular o valor de seno e cosseno de em função do comprimento da barra:
O valor de pode ser encontrado pelo teorema de Pitágoras:
Com isso, encontramos e :
Passo 5
Voltando para a equação que tínhamos encontrado anteriormente:
Substituindo os valores de e :
Resposta
Exercício Resolvido #11
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 27-1.44.
A luminária de é sustentada por três hastes de aço interligadas por um anel em . Determine o ângulo de orientação de de modo que a tensão normal média na haste seja duas vezes a tensão normal média na haste .
Qual é a intensidade da tensão em cada haste? O diâmetro de cada haste é dado na figura.
Passo 1
Galera, para começar esse problema que tal fazermos um diagrama de corpo livre? O ponto está sobre ação de três forças de tração:
O valor de uma dessas forças foi dado pelo exercício: a haste deve exercer uma força de tração suficiente para sustentar a luminária de no ponto . Isso significa que:
A partir daí vamos analisar quais serão as tensões internas e também vamos utilizar um pouquinho de trigonometria para resolver este problema, beleza?
Lembre-se que o exercício quer saber qual o ângulo para que . O exercício também quer saber os valores de , e nesse caso.
Passo 2
Que tal lembramos agora então a definição da tensão normal? É basicamente a força normal sobre a área:
Gente, nesse caso as trações são as próprias forças normais ok? Porque atuam no sentido axial. E são todas trativas porque esticam as hastes. Então vamos ter o seguinte:
Show de bola!
Mais e aí? Como vamos encontrar ?
- Vamos ter que fazer o equilíbrio de forças no ponto . Isso vai gerar um sistema de equações.
- Desse sistema de equações vamos encontrar , em função de ;
- Com isso e com as áreas e já calculadas, vamos encontrar e também em função de ;
- Finalmente, vamos usar a relação para encontrar o valor de !
Passo 3
Agora é hora do equilíbrio de forças no ponto :
Com ajuda da imagem acima, conseguimos fazer o equilíbrio de forças na vertical e na horizontal.
Só precisamos tomar o cuidado de decompor devidamente as forças e em suas componentes em e em !
Para a vertical, o equilíbrio de forças fica assim:
Calculando as componentes e substituindo :
Vamos guardar essa equação para o nosso futuro sistema de equações!
E agora, o equilíbrio de forças para a horizontal:
Calculando as componentes:
Com isso, nosso sistema de equações fica pronto:
Substituindo os valores de e nós vamos ter:
Reorganizando:
Passo 4
Pessoal, até dá para resolver esse sistema “na marra” mas vamos fazer de uma forma mais esperta. Para isso vamos trazer a seguinte relação:
Agora temos de calcular as áreas. As áreas , e podem ser calculadas a partir dos diâmetros , e .
Começando pelo cálculo das áreas das seções transversais usando a fórmula da área circular :
Substituindo o valor dos diâmetros:
Então se a gente substituir essas áreas na relação de tensões vamos ter:
Agora olha só o nosso sistema:
Substituindo a relação entre e encontrada na segunda equação vamos ter:
Logo,
Então já achamos a primeira parte do problema que é achar o ângulo . Agora temos de encontrar as tensões.
Passo 5
Com o ângulo encontrado, agora só falta calcular as tensões em cada haste. Para isso vamos precisar das tensões e . Para isso vamos substituir no nosso sistema:
Nós já sabemos que
Então vamos substituir na primeira equação junto com o valor do :
E o valor de será dado por:
Passo 6
Agora é só utilizar a equação da tensão normal média. Usando a fórmula da tensão normal média para a tensão na haste , :
Substituindo os valores e :
Para vamos ter:
Nós já temos a área e a força :
Substituindo:
E para :
A área e força são dadas por:
Substituindo: