Estado Triaxial (“3D”) de Tensões
Produzido por Pablo RicardoTeoria
Introdução
Dessa vez, vamos dizer que você é um(a) engenheiro(a) naval e descobriu que o ponto mais crítico do barco do seu cliente está submetido a um estado de tensões:
Sendo que, além disso, o choque da água ainda gera nesse ponto uma tensão normal no eixo :
...como mostra a imagem abaixo:
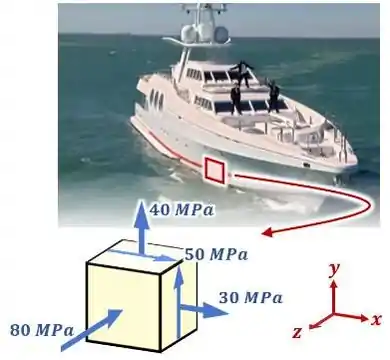
Com isso, nós deixamos de trabalhar com um estado plano de tensões, representado por um quadrado, e passamos a trabalhar com um estado triaxial ou 3D, representado por um cubo.
Agora...
Vamos dizer que o material desse ponto é um material que falha sempre por causa da tensão cisalhante .
Então, para saber se esse ponto vai falhar, você precisa descobrir:
Qual é a tensão cisalhante máxima nele?
Transformação de Tensões
De início, você pode pensar que a tensão cisalhante máxima nesse ponto é a de no plano , por ser a única tensão que existe nele:
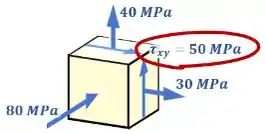
Mas aí você se lembra!
Essas tensões desenhadas no cubo são só as tensões nesse ponto quando ele está nessa orientação...
Mas se você rotacionar esse cubo (mudar a orientação dele), essas tensões vão se transformar:
- Uma parte das tensões normais podem virar tensões cisalhantes (e vice-versa);
- Ou uma parte de uma tensão em um eixo por virar tensão em outro eixo;
- Etc.
Assim, vai haver alguma orientação do ponto em que vai surgir uma tensão de cisalhamento máxima , possivelmente bem maior que a de .
Então...
Como é que a gente pode analisar as tensões em diferentes orientações desse ponto, para que a gente possa descobrir a tensão nele?
Círculo de Mohr para o Estado Triaxial de Tensões
A resposta está em utilizar o Círculo de Mohr, que, para um elemento “3D”, vai ser composto na realidade por 3 círculos.
Mas como assim?
Então...
Lá no estado plano de tensões, o que acontecia era que nós tinhamos 2 tensões principais ( e ) e o círculo de Mohr era o círculo que existia entre essas duas tensões:
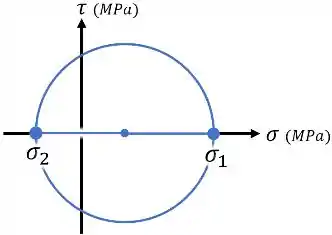
Agora, para o estado triaxial de tensões, nós temos 3 tensões principais:
- ou , a tensão principal “máxima”; (que fica mais à direita no gráfico)
- ou , a tensão principal intermediária;
- & ou , a tensão principal “mínima”; (que pode superar a máxima em intensidade e que fica à esquerda no gráfico)
E aí, entre essas 3 tensões principais, nós conseguimos desenhar 3 círculos:
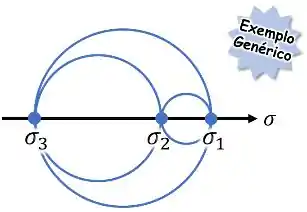
Juntos, esses 3 círculos são os nossos círculos de Mohr para um estado triaxial de tensões.
Beleza!
Mas como a gente faz para desenhar esses círculos em um caso real?

Vamos ver isso agora!
Como desenhar o Círculo de Mohr “3D”?
1° Caso - Caso Simplificado
Às vezes, o exercício vai nos fornecer um elemento 3D de tensões só com tensões normais , e . (Livre de qualquer tensão de cisalhamento!)
Como, por exemplo, caso a tensão de cisalhamento no nosso barco não existisse:
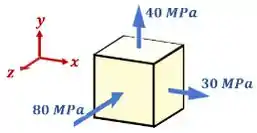
Mas espera aí!
As tensões principais são justamente aquelas que aparecem quando o elemento está livre de tensões de cisalhamento!!!!!
Então as tensões , e dadas pelo exercício já vão ser as tensões principais , e .
Só precisamos ordenar elas! ( precisa ser a máxima, a intermediária, etc.)
Aí, marcando essas 3 tensões em um gráfico , você consegue desenhar os 3 círculos entre elas:
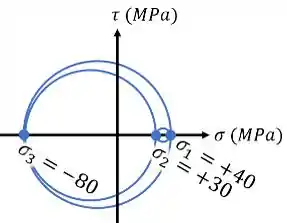
E pronto! Círculos de Mohr desenhados.
![]()
2° Caso - Caso Comum
Agora, nos exercícios mais difíceis, nós vamos ter um elemento com alguma tensão de cisalhamento em algum plano.
Pode ser uma , uma ou uma :
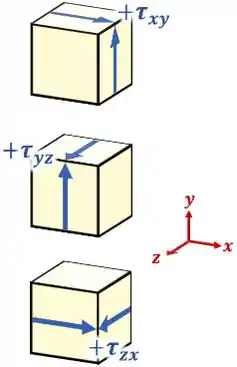
É o caso do ponto do nosso barco, por exemplo, onde temos uma :
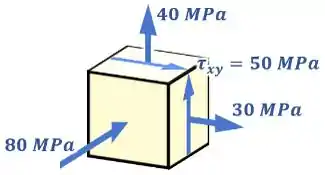
Nesse caso, podemos perceber uma coisa:
Se temos uma tensão , mas não tensões ou , isso significa que não há nenhum cisalhamento envolvendo o eixo .
E se o eixo já está livre de cisalhamento, então a tensão de nele já é uma tensão principal (ainda não sabemos qual).
Percebendo isso, podemos:
- Esquecer temporariamente desse eixo livre de cisalhamento;
- Olhar para o plano em que o cisalhamento ainda existe;
- & desenhar o círculo de Mohr para esse plano :
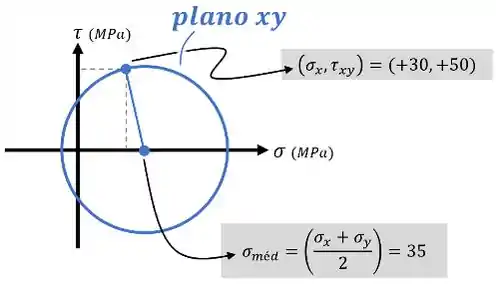
Aí, se antes nós já tinhamos identificado uma tensão principal, agora com esse círculo de Mohr para o plano identificamos as outras duas:
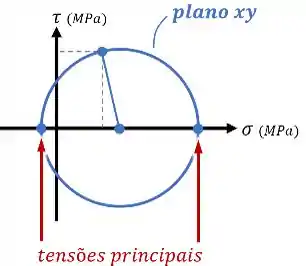
Assim, adicionando ao gráfico a tensão principal de que já tinhamos reconhecido anteriormente, conseguimos:
- Desenhar os outros dois círculos;
- & numerar as tensões principais,
Como na figura abaixo:
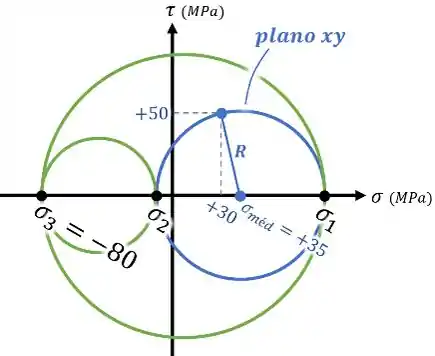
Por fim...
Ainda podemos calcular as tensões principais no círculo “plano ” calculando o raio desse círculo e depois fazendo :

Tensão de Cisalhamento Máxima Absoluta
Depois de entender tudo sobre o círculo de Mohr no caso triaxial, podemos voltar para a nossa pergunta inicial:
Qual é a tensão cisalhante máxima no ponto crítico do barco?
Para responder essa pergunta, basta olharmos para o ponto mais alto entre os 3 círculos que desenhamos:
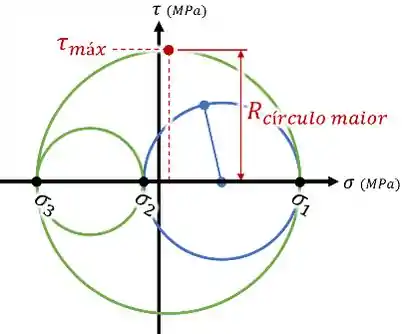
Nessa imagem, vemos que essa tensão cisalhante máxima é igual ao raio do círculo maior.
E o raio do círculo maior pode ser calculado dividindo o seu diâmetro por 2.
Dessa forma, dizemos que, em um estado de tensões triaxial, a tensão de cisalhamento máxima no ponto é sempre:
Uma Observação Final
Identificando os 3 Círculos
É comum que, depois de encontrarmos as tensões principais , e no elemento, a gente faça um desenho mostrando o elemento sob essas tensões principais:
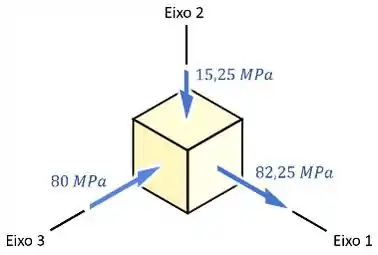
E nesse desenho, chamamos de “eixo 1” o eixo onde ocorre , “eixo 2” o eixo onde ocorre e “eixo 3” o eixo onde ocorre .
Daí que, alguns professores mais formais gostam que você identifique os 3 círculos do gráfico com base nesses eixos.
Nesses casos, fazemos isso assim:
- O círculo interno à esquerda vai representar sempre o “eixo 1”;
- O círculo externo o “eixo 2”;
- E o círculo interno à direita o “eixo 3”.
Como foi feito abaixo:
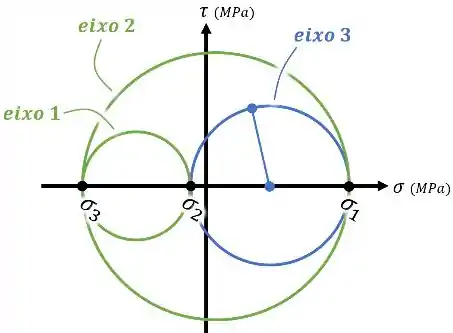
E o que isso significa?
Significa que cada círculo do gráfico representa o que acontece se a gente girar o elemento em volta daquele eixo.
Se a gente fosse girar o elemento em volta do “eixo 1”, por exemplo:
- A tensão vai permanecer intacta;
- Mas as tensões nas faces onde ocorriam e vão variar de acordo com o círculo “eixo 1”.
Círculo de Mohr para o Estado Triaxial de Tensões
Como desenhar o Círculo de Mohr “3D”?
Tensão de Cisalhamento Máxima Absoluta
Uma Observação Final
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 356-9.89.
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
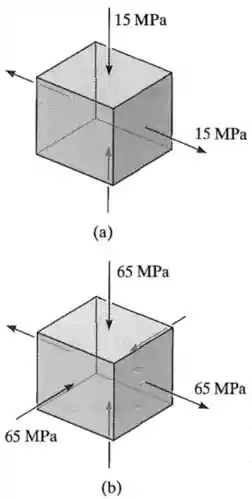
Passo 1
O que está acontecendo?
Tanto no item quanto no item , o exercício nos forneceu estados triaxiais de tensão em que não há nenhuma tensão de cisalhamento .
O que isso significa é que as tensões normais mostradas nesses elementos já são as tensões principais , e neles.
E o que é que o exercício quer?
Ele quer que a gente desenhe os três círculos de Mohr para cada um desses estados de tensão.
Então, o que devemos fazer para cada item é:
- Identificar e ordenar as tensões principais , e ;
- Marcar essas tensões em um gráfico ;
- & desenhar os três círculos entre esses pontos marcados.
Passo 2
Então vamos lá!
Começando pelo item :
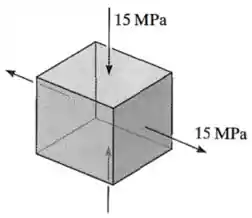
Nesse elemento, em uma direção nós temos uma tração de , em outra uma compressão de e em outra nenhuma tensão normal, ou seja, .
Sendo assim, vamos ter então tensões principais de , e .
Ordenando essas tensões, encontramos que:
Aí, marcando esses três pontos em um gráfico e desenhando círculos entre eles, obtemos a nossa resposta para o item , que é o desenho abaixo:
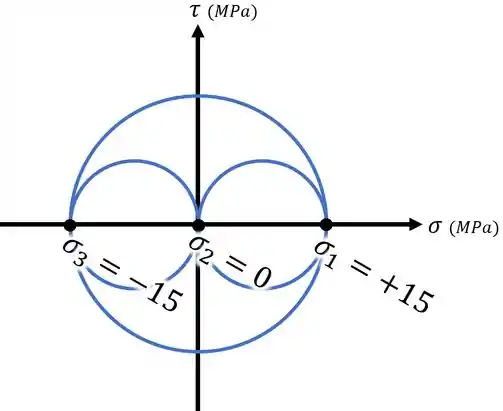
Passo 3
Já no item :
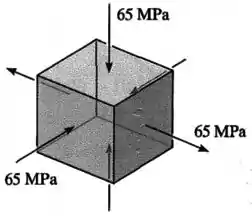
...nós temos em duas direções compressões de , e na outra direção uma tração de .
Dessa forma, nossas tensões principais vão ser de , e .
Ordenando essas tensões, encontramos que:
Aí, marcando esses três pontos em um gráfico e desenhando círculos entre eles, obtemos a nossa resposta para o item , que é o desenho abaixo:
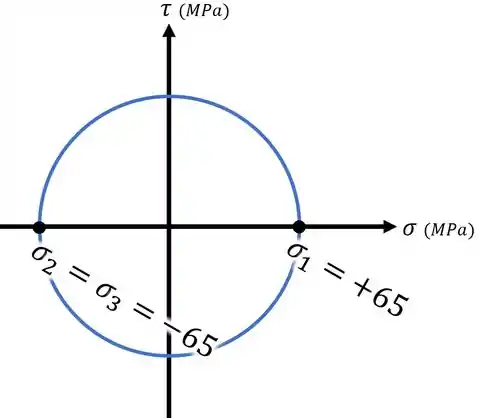
Observação:
Esse exemplo é interessante pois dá para ver nele como um dos círculos (o círculo formado entre e ) se reduziu a um ponto, fazendo com que os outros dois círculos fossem coincidentes.
E aí com isso, ficamos com essa situação em que aparentemente só temos 1 círculo de Mohr.
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 357-9.91.
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
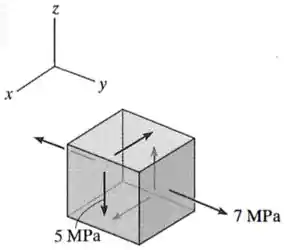
Passo 1
O que está acontecendo?
Nesse exercício, nós temos um elemento 3D de tensões em que existe:
- Uma tensão de cisalhamento no plano , que é negativa por não estar apontando para o primeiro quadrante entre os eixos e ;
- E uma tensão normal no eixo , que é positiva por ser de tração.
Aí, para esse elemento, como não existe nenhuma tensão de cisalhamento ou envolvendo o eixo , podemos concluir que o eixo já está livre de cisalhamento.
Isso significa que a tensão no eixo já é então uma das tensões principais desse elemento. (Só não sabemos qual...)
E o que é que o exercício quer?
Ele quer que a gente determine as tensões principais , e para esse elemento, além da tensão de cisalhamento máxima absoluta para ele:
Nós já conhecemos uma das tensões principais: a tensão de que ocorre no eixo , livre de cisalhamento.
Então para determinar as outras duas tensões principais, nós podemos esquecer do eixo e focar no que resta, que é o plano :
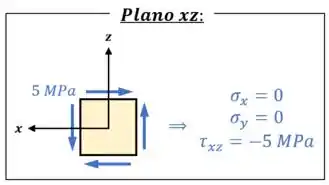
Calculando a tensão normal média para esse plano e fazendo o círculo de Mohr para ele, vamos conseguir calcular o raio desse círculo, para, em seguida, determinarmos as suas tensões principais:
Aí, com essas duas tensões principais do plano , mais a tensão principal do eixo , vamos conseguir:
- Desenhar os três círculos de Mohr para esse estado triaxial de tensões;
- Ordenar as tensões principais encontradas, definindo assim as tensões principais , e ;
- E calcular a tensão de cisalhamento máxima absoluta nesse ponto, .
Passo 2
Então vamos começar fazendo o círculo de Mohr do plano .
Lembra aí!
Para fazer isso, precisamos calcular para esse plano:
Feito isso, podemos marcar esse ponto e o ponto em um gráfico e usar esses pontos para desenhar o nosso círculo:
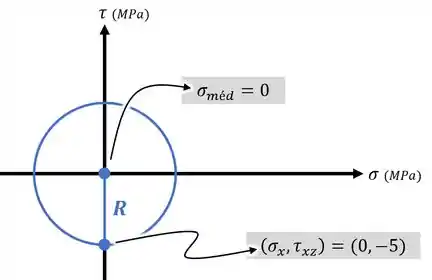
Passo 3
Agora, usando o círculo que acabamos de fazer, conseguimos identificar que:
E aí, podemos fazer que:
E substituir e para encontrarmos as tensões principais do plano :
Isso significa que o nosso elemento 3D, além da tensão principal de que já tínhamos identificado, ainda tem uma tensão principal de e outra de .
Passo 4
Agora que sabemos as três tensões principais do nosso elemento 3D, podemos complementar o círculo de Mohr que fizemos para o plano com elas.
Fazendo isso, vamos obter os três círculos de Mohr para o nosso elemento 3D e ao mesmo tempo identificar qual tensão principal é qual (, ou ):
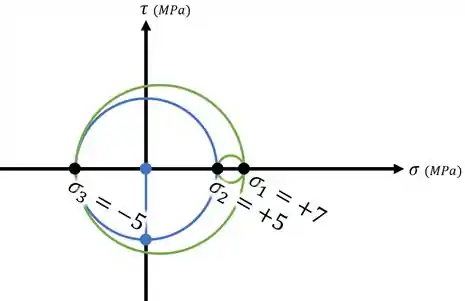
Se quisermos, ainda podemos identificar os círculos:
- O círculo interno à esquerda, entre as tensões principais e , descreve o que ocorre se a gente rotacionar o elemento em volta do “eixo 1” (aquele em que ocorre a tensão principal );
- O círculo externo, entre e , descreve a rotação em volta do “eixo 2”;
- E o círculo interno à direita, a rotação em volta do “eixo 3”:
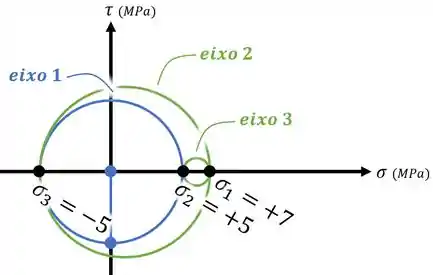
Passo 5
Por fim, podemos calcular a tensão de cisalhamento máxima absoluta nesse elemento fazendo:
Aí, substituindo e , vamos ter:
E pronto!
Está resolvido o nosso exercício.
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 356-9.90.
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
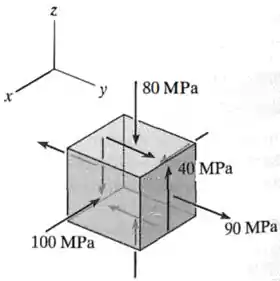
Passo 1
O que está acontecendo?
Nesse exercício, temos um elemento 3D de tensões com uma tensão de cisalhamento:
...no plano , além de tensões normais em cada eixo:
Aí, para esse elemento, como não existe nenhuma tensão de cisalhamento ou envolvendo o eixo , podemos concluir que esse eixo já está livre de cisalhamento.
Isso significa que a tensão no eixo já é então uma das tensões principais desse elemento. (Só não sabemos qual...)
E o que é que o exercício quer?
Ele quer que a gente determine as tensões principais , e para esse elemento, além da tensão de cisalhamento máxima absoluta para ele:
Nós já conhecemos uma das tensões principais: a tensão de que ocorre no eixo , livre de cisalhamento.
Então para determinar as outras duas tensões principais, nós podemos esquecer do eixo e focar no que resta, que é o plano :
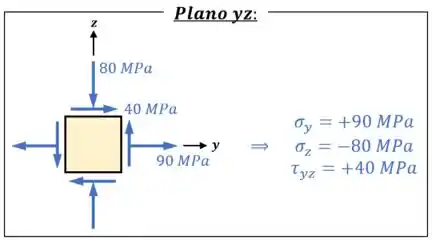
Calculando a tensão normal média para esse plano e fazendo o círculo de Mohr para ele, vamos conseguir calcular o raio desse círculo, para, em seguida, determinarmos as suas tensões principais:
Aí, com essas duas tensões principais do plano , mais a tensão principal do eixo , vamos conseguir:
- Desenhar os três círculos de Mohr para esse estado triaxial de tensões;
- Ordenar as tensões principais encontradas, definindo assim as tensões principais , e ;
- E calcular a tensão de cisalhamento máxima absoluta nesse ponto, .
Passo 2
Então vamos começar fazendo o círculo de Mohr do plano .
Lembra aí!
Para fazer isso, precisamos calcular para esse plano:
Feito isso, podemos marcar esse ponto e o ponto em um gráfico e usar esses pontos para desenhar o nosso círculo:
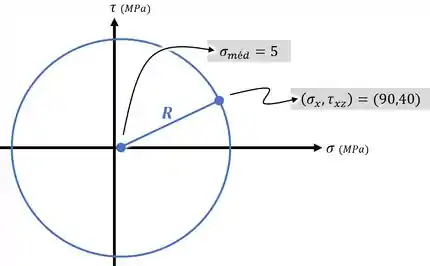
Passo 3
Agora, usando o círculo que acabamos de fazer, conseguimos usar o teorema de Pitágoras para determinarmos o valor do seu raio :
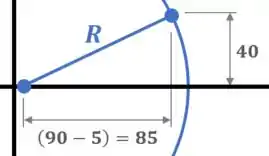
Fazendo isso, teremos que:
O que significa que:
E aí, podemos fazer que:
E substituir e para encontrarmos as tensões principais desse plano :
Daí que, calculando essa equação acima, encontramos que uma das tensões principais desse plano é de e que a outra é de .
Isso significa que o nosso elemento 3D, além da tensão principal de que já tinhamos identificado, ainda tem uma tensão principal de e outra de .
Passo 4
Agora que sabemos as 3 tensões principais do nosso elemento 3D, podemos complementar o círculo de Mohr que fizemos para o plano com elas.
Fazendo isso, vamos obter os três círculos de Mohr para o nosso elemento 3D e ao mesmo tempo identificar qual tensão principal é qual (, ou ):
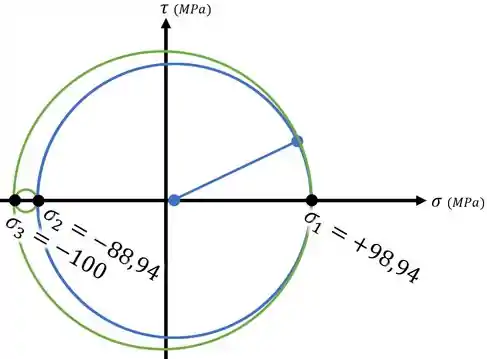
Passo 5
Por fim, podemos calcular a tensão de cisalhamento máxima absoluta nesse elemento fazendo:
Aí, substituindo e , vamos ter:
E pronto!
Está resolvido o exercício.
Resposta
Exercício Resolvido #4
Elaboração própria
Dado o elemento infinitesimal dado abaixo, determine as tensões normais e cisalhantes absolutas do elemento.
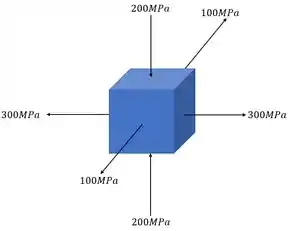
Passo 1
Aqui podemos ver que se trata de um exercício sobre estado triaxial de tensões. Como não há tensões cisalhantes em nenhum dos planos, sabemos que esses planos já representam planos principais.
Mas aqui temos que lembrar o seguinte
Passo 2
Agora que já sabemos quais são as tensões principais, e também sabemos que o nosso elemento por não ter cisalhante também só possui tensões principais, basta relacionar todas as tensões.
Dessa forma teremos que
Já com esses valores podemos marcar os pontos de tensões principais
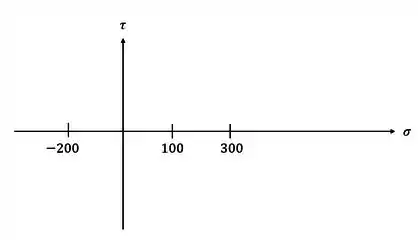
Já com isso em mãos basta apenas desenhar os círculos de Mohr
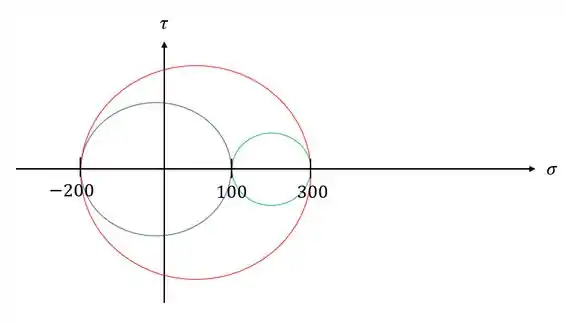
Passo 3
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por
Resposta
Exercício Resolvido #5
Elaboração própria
Dado o elemento mostrado abaixo, determine as tensões normais e cisalhantes absolutas.
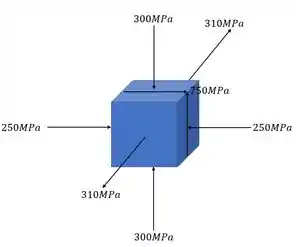
Passo 1
Podemos ver que se trata de uma questão em que o nosso elemento possui tensões cisalhantes em suas faces.
Quando há tensões cisalhantes, não podemos considerar os planos com essas tensões como planos principais.
O que sabemos é que o plano sem tensão cisalhante de fato representa um plano principal, mas nesse caso como não sabemos qual o valor dos outros dois planos só podemos afirmar isso até esse momento, ou seja,
Passo 2
Já sabemos que um dos planos se trata de um plano principal, mas como fazemos os outros dois também serem?
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
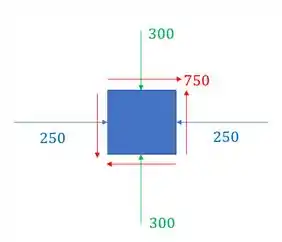
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 3
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Organizando teremos que
Passo 4
Agora vamos desenhar os círculos de Mohr para as nossas tensões
Primeiro vamos marcar os pontos
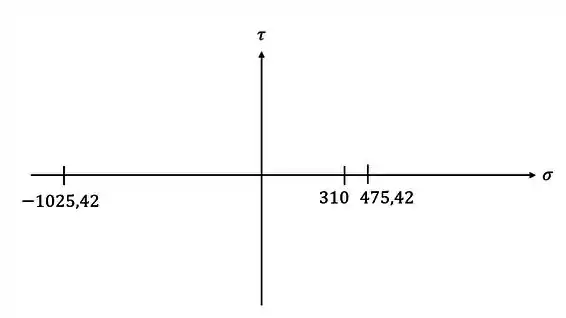
Agora vamos desenhar os círculos de Mohr
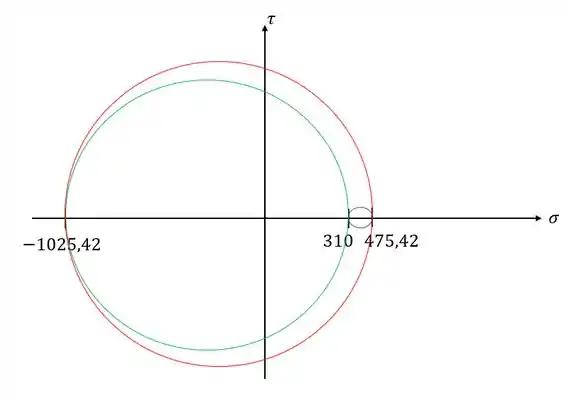
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por
Resposta
Exercício Resolvido #6
Elaboração própria
A fossa das Marianas é o local mais profundo dos oceanos, atingindo uma profundidade de 11034m. Considere que um submarino é feito de um material com resistência ao cisalhamento de e resistência ao normal de . Sabendo que a pressão de água é calculada pela fórmula P=dgh e que essa pressão age igualmente em todas a direções do nosso elemento tridimensional. A água não oferece resistência cisalhante. Nas direções x e z surgem acréscimos de tensões de -100Mpa e 85Mpa respectivamente, devido a tensões internas causadas pela idade do submarino. Sabendo disso, determine se o material constituinte desse submarino suportaria chegar ao fundo da fossa das Marianas.
Passo 1
Primeiro devemos desenhar o nosso elemento tridimensional e acrescentar as tensões presentes no nosso elemento.
Primeiro colocar a pressão devido a ação da água.
O valor dessa pressão é calculado por
Logo, em cada face haverá ação de 110Mpa comprimindo, agora vamos acrescentar as tensões ditas no enunciado na direção x e z.
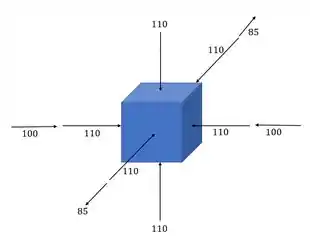
Somando as tensões na mesma direção teremos que
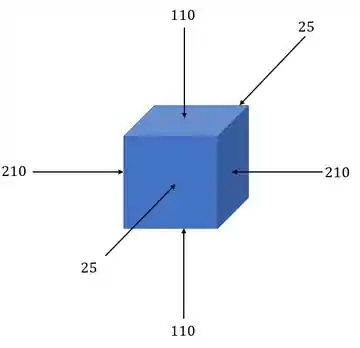
Passo 2
Agora que já sabemos quais são as tensões principais, e também sabemos que o nosso elemento por não ter cisalhante também só possui tensões principais, basta relacionar todas as tensões.
Dessa forma teremos que
Desenhando os círculos de Mohr
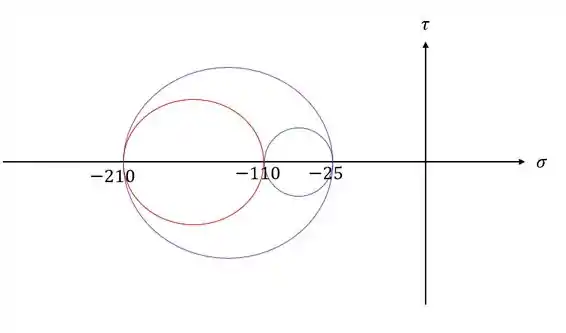
Passo 3
Agora vamos analisar a resistência ao normal, sabemos que
Como a resistência da nossa peça ao esforço normal é de 300Mpa, sabemos que o material chegara ao fundo da fossa das marianas sem romper pelos esforços normais.
Agora analisando o cisalhante teremos que
Como a resistência ao cisalhamento da nossa peça é de 90 Mpa, sabemos que o material do nosso submarino rompera pelo esforço cisalhante.
Resposta
Pelos cálculos vimos que o submarino não chagará ao fundo da fossa das marianas pois acabaria tendo o seu material constituinte rompendo pela ação do esforço cisalhante máximo de 92,5 Mpa.
Exercício Resolvido #7
Elaboração própria
Um avião está sujeito a esforços solicitantes. Um material da asa do avião suporta altos esforços normais, porém suporta apenas 200Mpa de tensões cisalhantes. Se um elemento infinitesimal tridimensional estiver submetido aos esforços dados abaixo, a asa suportará as tensões ou romperá?
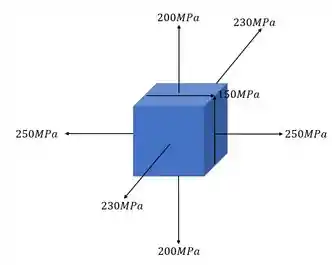
Passo 1
Sabemos que como apresenta-se tensão cisalhante em alguns planos, estes não poderão ser considerados planos principais.
O que podemos afirmar é que o plano sem tensões cisalhantes é de fato um plano principal, podemos então afirmar que
Mas como determinar as tensões principais referentes aos outros planos?
Passo 2
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 3
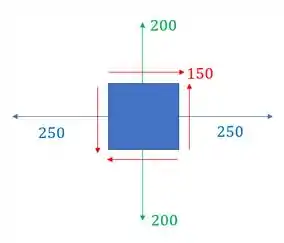
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Organizando teremos que
Passo 4
Desenhando o círculo de Mohr teremos que
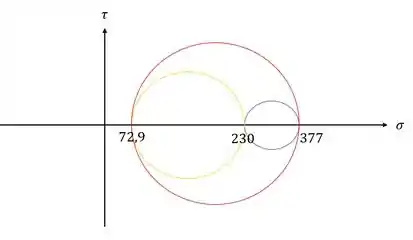
Já foi dito no enunciado que a resistência a esforços normais é muito grande, logo, não é necessário analisar esses esforços.
Mas a resistência ao cisalhante precisa ser analisada, basta então fazer a seguinte analise
Como a resistência a ação do cisalhante é dada por 200Mpa, percebemos que a asa do nosso avião suportará a ação dos esforços solicitantes sem que ocorra rompimento.
Resposta
A asa do avião suportará os esforços solicitantes pois a máxima tensão cisalhante alcançada é de 152,1 Mpa mas a resistência suportada é de até 200Mpa
Exercício Resolvido #8
Elaboração própria
Uma barra de madeira será submetida a um carregamento triaxial que pode causar o seu rompimento. Sabendo que em um determinado momento foi analisado o seguinte elemento 3D retirado da barra no momento em que a mesma foi submetida ao carregamento. Sabendo que a barra possui e , determine se a barra suportaria ou não o carregamento assinalado.
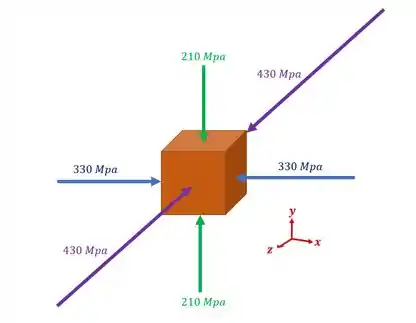
Passo 1
Aqui podemos ver que se trata de um exercício sobre estado triaxial de tensões. Como não há tensões cisalhantes em nenhum dos planos, sabemos que esses planos já representam planos principais.
Mas aqui temos que lembrar o seguinte
Passo 2
Agora que já sabemos quais são as tensões principais, e também sabemos que o nosso elemento por não ter cisalhante também só possui tensões principais, basta relacionar todas as tensões.
Dessa forma teremos que
Já com esses valores podemos marcar os pontos de tensões principais
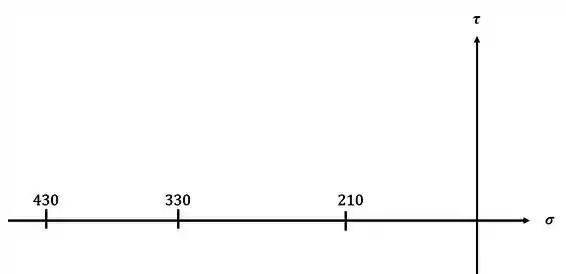
Já com isso em mãos basta apenas desenhar os círculos de Mohr
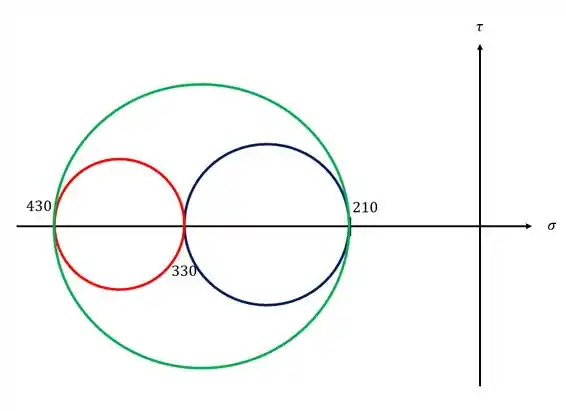
Passo 3
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por
Agora vamos pegar a resistência do nosso material, sabemos que
Sabemos que a nossa tensão máxima é
Que é menor que a nossa tensão admissível, ou seja, não ocorre rompimento da peça pelo efeito da tensão Normal.
Também sabemos que
Que apesar de estar próximo da nossa tensão admissível, não a ultrapassa, logo a nossa peça também está segura com relação a tensão cisalhante.
Resposta
Não ocorre rompimento da peça pois
Exercício Resolvido #9
Elaboração própria
Uma barra de aço possui resistência ao cisalhamento de e para o normal. Considerando a pior situação para a peça carregada abaixo, determine o fator de segurança dessa peça para o caso da tensão cisalhante e da tensão norma.
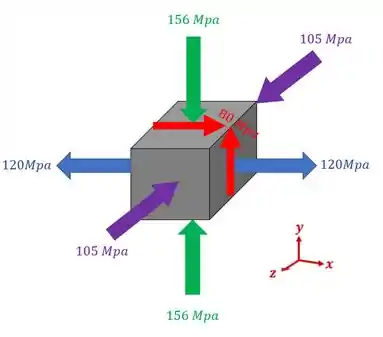
Passo 1
Podemos ver que se trata de uma questão em que o nosso elemento possui tensões cisalhantes em suas faces.
Quando há tensões cisalhantes, não podemos considerar os planos com essas tensões como planos principais.
O que sabemos é que o plano sem tensão cisalhante de fato representa um plano principal, mas nesse caso como não sabemos qual o valor dos outros dois planos só podemos afirmar isso até esse momento, ou seja,
Passo 2
Já sabemos que um dos planos se trata de um plano principal, mas como fazemos os outros dois também serem?
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
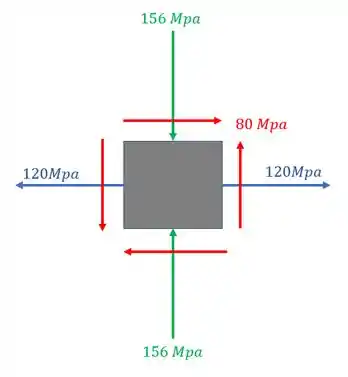
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 3
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Juntando o que já tínhamos calculado teremos
Organizando teremos que
Passo 4
Agora vamos desenhar os círculos de Mohr para as nossas tensões
Primeiro vamos marcar os pontos
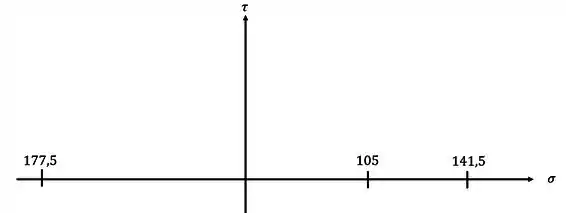
Agora vamos desenhar os círculos de Mohr
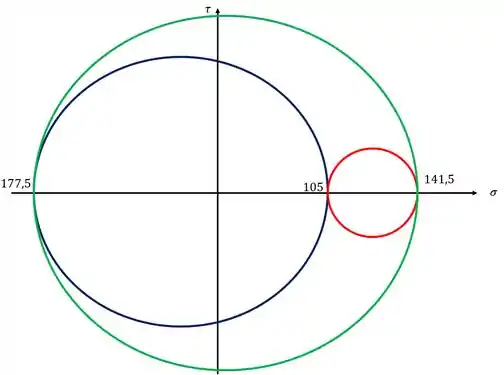
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Calculando os fatores de segurança, teremos