Resolva o circuito RLC
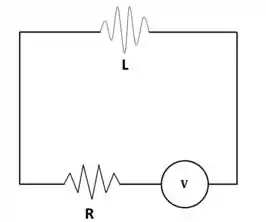
Sabendo que as quedas de tensão são:
E que a força eletromotriz da fonte é:
Faça
Passo 1
Pela teoria de Kirchoff, a tensão fornecida à um circuito fechado deve ser igual as quedas de tensões ao longo dele, assim:
Pela definição de corrente:
Subtituindo isso na EDO:
Derivando tudo com relação ao tempo:
Não esquece da regra da cadeia: (
Bem bem, tá quase com a cara que a gente gosta, vamos dividir tudo por :
Beleza, vamos escrever agora em função das variáveis que ele definiu:
Agora temos que resolver essa parada ae né? Simbora
Passo 2
Resolver a EDO homogênea!
Fazendo a equação característica:
Bem, a resposta varia de acordo com o sinal do cara dentro da raiz, podemos separa em casos,
Lembrando que, pelas propriedades físicas usadas, o
Pensa bem, o sistema está impondo uma voltagem oscilante no sistema, então uma solução de resposta da corrente oscilando parece justo se o amortecimento não for muito grande. O que expressaria oscilação seria para o caso , porque ae a solução seria uma combinação de seno com cosseno, o que representa bem o que queremos.
Assim a solução da equação homogênea é:
Galera, paranauê bolado, você pode juntar esse e :
Assim fica:
Basicamente trocamos as duas constantes para determinar : e por e
Passo 3
A carona da função é do outro lado, né? Então podemos chutar uma solução particular desse tipo:
Como a homogênea é multiplicada por exponencial, esse tipo de solução é viável para a particular, não tem necessidade de multiplica-la por nada, assim:
Substituindo em:
Obtemos:
Para gigante, né ? O.o ...vamos juntar o que tem cosseno e o que tem seno:
Daí temos que:
Que doidera, né?!
Mas olha, da primeira equação nós temos que:
Substituindo isso na segunda equação:
Assim:
Logo
Então :
Encontrar a cara da solução particular:
Ficou:
Passo 4
Então a solução geral é: