Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Modelagem – Circuito RLC

Ver Todos os Exercícios

Teoria

Introdução

Uma modelagem muito comum que vamos ter são os circuitos elétricos envolvendo 1 indutor, 1 resistor e 1 capacitor.

Aqui para chegar nas equações se usa as Leis de Kirchhoff. Não vamos focar nas explicações físicas para isso tudo, o importante aqui é saber como são os circuitos e chegar nas modelagens da corrente ou da carga. Para chegar no Circuito RLC vai ser uma mistura do circuito L-R e R-C. Vamos olhar rapidinho como eles são.

Circuito em série L-R

Um circuito desse vai ser representado assim.

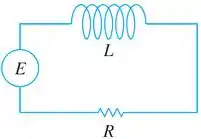
Esses circuitos vão conter um indutor e um resistor. Aqui vamos ter a EDO para chegar na função da corrente em função do tempo. Essa EDO vai ser

L d i d t + R i ( t ) = E ( t )

A indutância, L , e a resistência, R , podem ser definidas por constantes ou por funções de t .

Esse E t é a função da Tensão que passa pelo circuito.

Circuitos em série R-C

Um circuito desse vai ser representado assim.

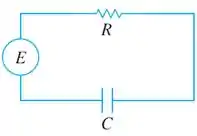
Esses circuitos vão ter um capacitor e um resistor. Aqui vamos ter a EDO para chegar na função da carga no capacitor q t   em função do tempo. Essa EDO vai ser

R d q d t + 1 C q ( t ) = E t

A capacitância, C , e a resistência, R , podem ser definidos por constantes ou por funções de t .

Esse E t é a função da Tensão que passa pelo circuito.

Circuito RLC

Quando temos envolvendo 1 indutor, 1 resistor e 1 capacitor o nosso circuito vai ser

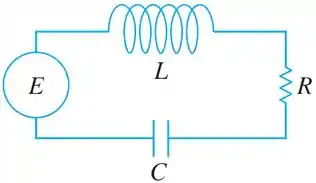
Aqui a nossa EDO vai ficar uma junção das duas ali de cima

L d i d t + R i ( t ) + 1 C q ( t ) = E ( t )

O problema aqui é que temos duas variáveis, a corrente e a carga. Vamos usar a relação entre elas

i = d q d t

Aí passamos a ter uma EDO de 2ª Ordem.

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

Aqui temos a EDO para q t , se ele quiser i t basta fazer a primeira derivada de q t em relação ao tempo.

Quando E t = 0 , as vibrações elétricas do circuito são ditas livres. Nossa EDO se reduz a:

L d 2 q d t 2 + R d q d t + 1 C q = 0

Já estudamos EDO’s de 2° ordem aplicados a problemas físicos. Lá em Movimento Harmônico Amortecido (MHA) a EDO era a seguinte:

x ¨ + 2 λ x ˙ + ω 0 2 x = 0

Deu pra lembrar?! Tínhamos 3 casos :

  • Criticamente Amortecido, quando ∆ = 0 .
  • Superamortecido, quando ∆ > 0 .
  • Subamortecido, quando ∆ < 0 .

Aqui não vai ser diferente. Voltando a nossa EDO de 2° Ordem:

L d 2 q d t 2 + R d q d t + 1 C q = 0

A equação auxiliar vai ser:

L r 2 + R r + 1 c = 0

Então, podemos encontrar:

∆ = R 2 - 4 L c

Logo, para R ≠ 0 , temos 3 casos:

  • Criticamente amortecido: ∆ = 0

    • O que implica em R 2 - 4 L c = 0

  • Superamortecido: ∆ > 0

    • O que nos leva a R 2 - 4 L c > 0

  • Subamortecido: ∆ < 0

Resultando em R 2 - 4 L c < 0

Observação:

Quando E t = 0 e R = 0 , dizemos que o circuito é não amortecido, a resposta do circuito é harmônica simples.

Partiu exercícios?!

Circuitos em série R-C

Circuito RLC

Exercícios Resolvidos

Exercício Resolvido #1

UERJ - Cálculo 3 - Lista 7 Fernando Lopes

Resolva o circuito RLC

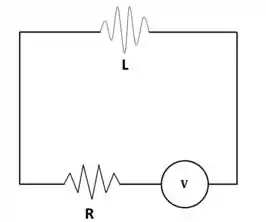
Sabendo que as quedas de tensão são:

I n d u t o r     L d I d t R e s i s t o r     R I C a p a c i t o r   Q C

E que a força eletromotriz da fonte é:

E t = E 0 sen ⁡ ( w s t )

Faça

2 b = R L             w 0 2 = 1 L C             F = w 0 E 0 L

Passo 1

Pela teoria de Kirchoff, a tensão fornecida à um circuito fechado deve ser igual as quedas de tensões ao longo dele, assim:

L d I d t + R I + Q C = E 0 sen ⁡ ( w s t )

Pela definição de corrente:

I = d Q d t → d Q = I d t →     Q = ∫ I d t

Subtituindo isso na EDO:

L d I d t + R I + 1 C ∫ I d t = E 0 sen ⁡ ( w s t )

Derivando tudo com relação ao tempo:

L d 2 I d t 2 + R d I d t + I C = E 0 w s cos ⁡ ( w s t )

Não esquece da regra da cadeia: ( E 0 sen ⁡ ( w s t ) ) ' = E 0 w s cos ⁡ ( w s t )

Bem bem, tá quase com a cara que a gente gosta, vamos dividir tudo por L :

d 2 I d t 2 + R L d I d t + 1 C L I = E 0 w s L cos ⁡ w s t

Beleza, vamos escrever agora em função das variáveis que ele definiu:

d 2 I d t 2 + 2 b d I d t + w 0 2 I = F cos ⁡ w s t

Agora temos que resolver essa parada ae né? Simbora

Passo 2

Resolver a EDO homogênea!

d 2 I d t 2 + 2 b d I d t + w 0 2 I = 0

Fazendo a equação característica:

r 2 + 2 b + w 0 2 = 0

r 1 = - 2 + 4 b 2 - 4 w 0 2 2 = - 2 + 4 b 2 - w 0 2 2 = - 2 + 2 b 2 - w 0 2 2 = - 1 + b 2 - w 0 2 r 2 = - 2 - 4 b 2 - 4 w 0 2 2 = - 2 - 4 b 2 - w 0 2 2 = - 2 - 2 b 2 - w 0 2 2 = - 1 - b 2 - w 0 2

Bem, a resposta varia de acordo com o sinal do cara dentro da raiz, podemos separa em 3 casos,

b 2 - w 0 2 > 0 ⇒ b > w 0

b 2 - w 0 2 = 0 ⇒ b = w 0

b 2 - w 0 2 < 0 ⇒ b < w 0

Lembrando que, pelas propriedades físicas usadas, o b > 0

Pensa bem, o sistema está impondo uma voltagem oscilante no sistema, então uma solução de resposta da corrente oscilando parece justo se o amortecimento não for muito grande. O que expressaria oscilação seria para o caso b < w 0 , porque ae a solução seria uma combinação de seno com cosseno, o que representa bem o que queremos.

r 1 = - 1 + i w 0 2 - b 2

r 1 = - 1 - i w 0 2 - b 2

Assim a solução da equação homogênea é:

I h = e - t c 1 cos ⁡ w 0 2 - b 2 . t + c 2 sen ⁡ w 0 2 - b 2 . t

Galera, paranauê bolado, você pode juntar esse s e n e c o s :

A sen ⁡ ( c t ) + B cos ⁡ ( c t ) = A 2 + B 2 cos ⁡ c t + ϕ = C cos ⁡ c t + ϕ

Assim fica:

c 1 cos ⁡ w 0 2 - b 2 . t + c 2 sen ⁡ w 0 2 - b 2 . t = A cos ⁡ w 0 2 - b 2 . t + ϕ

Basicamente trocamos as duas constantes para determinar :   c 1 e c 2   por A e ϕ

Passo 3

A carona da função é F cos ⁡ w s t do outro lado, né? Então podemos chutar uma solução particular desse tipo:

I p = k 1 . cos ⁡ w s t + k 2 . sen ⁡ ( w s t )

Como a homogênea é multiplicada por exponencial, esse tipo de solução é viável para a particular, não tem necessidade de multiplica-la por nada, assim:

I p ' = - k 1 w s sen ⁡ w s t + k 2 w s . cos ⁡ ( w s t )

I p ' ' = - k 1 w s 2 cos ⁡ w s t - k 2 w s 2 sen ⁡ w s t

Substituindo em:   d 2 I d t 2 + 2 b d I d t + w 0 2 I = F cos ⁡ w s t

Obtemos:

- k 1 w s 2 cos ⁡ w s t - k 2 w s 2 sen ⁡ w s t - 2 b k 1 w s sen ⁡ w s t + 2 b k 2 w s . cos ⁡ w s t + w 0 2 k 1 . cos ⁡ w s t + w 0 2 k 2 . sen ⁡ w s t = F cos ⁡ w s t

Para gigante, né ? O.o ...vamos juntar o que tem cosseno e o que tem seno:

sen ⁡ w s t - k 2 w s 2 - 2 b k 1 w s + w 0 2 k 2 + cos ⁡ w s t - k 1 w s 2 + 2 b k 2 w s + w 0 2 k 1 = F cos ⁡ w s t

Daí temos que:

- k 2 w s 2 - 2 b k 1 w s + w 0 2 k 2 = 0 →   k 2 w 0 2 - w s 2 = 2 b k 1 w s

- k 1 w s 2 + 2 b k 2 w s + w 0 2 k 1 = F →   - k 1 w 0 2 - w s 2 + 2 b k 2 w s = F

Que doidera, né?!

Mas olha, da primeira equação nós temos que:

k 2 w 0 2 - w s 2 = 2 b k 1 w s → k 1 = k 2 2 b w s w 0 2 - w s 2

Substituindo isso na segunda equação:

- k 2 2 b w s w 0 2 - w s 2 2 + 2 b k 2 w s = F Assim:

k 2 2 b w s - w 0 2 - w s 2 2 2 b w s = F

Logo k 2 :

k 2 = F 2 b w s - w 0 2 - w s 2 2 2 b w s = 2 b w s F 4 b 2 w s 2 - w 0 2 - w s 2 2

Então k 1 :

k 1 = k 2 2 b w s w 0 2 - w s 2 = w 0 2 - w s 2 F 4 b 2 w s 2 - w 0 2 - w s 2 2

Encontrar a cara da solução particular: I p = k 1 . cos ⁡ w s t + k 2 . sen ⁡ ( w s t )

Ficou:

I p = w 0 2 - w s 2 F 4 b 2 w s 2 - w 0 2 - w s 2 2 . cos ⁡ w s t + 2 b w s F 4 b 2 w s 2 - w 0 2 - w s 2 2 . sen ⁡ ( w s t )

I p = F 4 b 2 w s 2 - w 0 2 - w s 2 2 . ( w 0 2 - w s 2 cos ⁡ w s t + 2 b w s sen ⁡ w s t )

Passo 4

Então a solução geral I = I p + I h é:

I = F 4 b 2 w s 2 - w 0 2 - w s 2 2 . ( w 0 2 - w s 2 cos ⁡ w s t + 2 b w s sen ⁡ w s t )

Resposta

I ( t ) = F 4 b 2 w s 2 - w 0 2 - w s 2 2 . ( w 0 2 - w s 2 cos ⁡ w s t + 2 b w s sen ⁡ w s t )

Exercício Resolvido #2

Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON, 2001, pp. 264 - 4

Determine se o circuito L-R-C dado é criticamente amortecido, subamortecido ou superamortecido:

L = 1   henry, R = 20   ohms e C = 0,01 farad

Passo 1

Vimos na teoria que, pela lei de Kirchhoff das tensões, o circuito RLC se reduz a EDO de 2° ordem:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

Passo 2

Agora vamos achar os valores que precisamos.

Como estamos interessados em saber se o sistema é criticamente amortecido, subamortecido ou superamortecido, temos que analisar o Δ da equação homogênea, então fazemos E t = 0

Temos ainda:

L = 1   henry, R = 20   ohms e C = 0,01 farad

Substituinido na EDO temos:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

1 d 2 q d t 2 + 20 d q d t + 1 0,01 q = 0

Passo 3

A equação auxiliar é:

1 r 2 + 20 r + 1 0,01 = 0

Calculando ∆ temos:

∆ = 20 2 - 4 1 100 = 400 - 400 = 0

Portanto, o circuito é criticamente amortecido.

Resposta

Criticamente amortecido.

Exercício Resolvido #3

Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON, 2001, pp. 264 - 5

Encontrar carga no capacitor em um circuito em série L-R-C no instante t = 0,01 segundo quando L = 0,05   h e n r y , R = 2   o h m s , C = 0,01   f a r a d ,   E t = 0   v o l t , q 0 = 5   c o u l u m b s e i 0 = 0   a m p e r . Determine o primeiro instante no qual a carga do capacitor é zero.

Passo 1

Vimos na teoria que, pela lei de Kirchhoff das tensões, o circuito RLC se reduz a EDO de 2° ordem:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

Passo 2

Agora, vamos substituir os valores dados:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

0,05 d 2 q d t 2 + 2 d q d t + 1 0,01 q = 0

Passo 3

A equação auxiliar é:

0,05 r 2 + 2 r + 1 0,01 = 0

Calculando ∆ temos:

∆ = 2 2 - 4 0,05 100 = - 16

Portanto as raízes são:

r 1 = - 2 + 4 i 0,1 = - 20 + 40 i

r 2 = - 2 - 4 i 0,1 = - 20 - 40 i

Passo 4

A solução da EDO é da forma:

q t = e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t

Pois estamos no caso em que ∆ < 0

Passo 5

Podemos determinar as constantes usando as condições iniciais:

q 0 = 5

i 0 = 0

Substituindo a primeira informação:

q t = e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t

q 0 = e - 20 0 c 1 cos ⁡ 40 . 0 + c 2 s e n 40 . 0 = c 1

Chegamos então a:

q 0 = c 1 = 5

c 1 = 5

Vamos usar a segunda informação:

i 0 = 0  

Porém sabemos que:

i = d q d t

Portanto, usando a regra do produto temos:

i t = - 20 e - 20 t 5 cos ⁡ 40 t + c 2 s e n 40 t + - 5 . 40 s e n 40 t + 40 c 2 cos ⁡ 40 t e - 20 t

Ajeitando:

i t = e - 20 t - 100 cos ⁡ 40 t - 20 c 2 s e n 40 t - 200 s e n 40 t + 40 c 2 cos ⁡ 40 t  

Usando i 0 = 0 temos:

i 0 = e - 20 0 - 100 cos ⁡ 0 - 20 c 2 s e n 0 - 200 s e n 0 + 40 c 2 cos ⁡ 0

i 0 = - 100 + 40 c 2 = 0

Temos então:

c 2 = 5 2

A solução da EDO fica então:

q t = e - 20 t 5 cos ⁡ 40 t + 5 2 s e n 40 t

Passo 6

Calculando q 0,01 temos:

q 0,01 = e - 20 0,01 5 cos ⁡ 40 . ( 0,01 ) + 5 2 s e n 40 ( 0,01 )  

Temos:

q 0,01 = 4,5676   c o u l u m b s

Passo 7

Agora só falta determinar o primeiro instante em que a carga do capacitor é zero. Queremos encontrar o instante que q t = 0 .

Temos então:

q t = e - 20 t 5 cos ⁡ 40 t + 5 2 s e n 40 t = 0  

Repare que temos então duas possibilidades:

5 cos ⁡ 40 t + 5 2 s e n 40 t = 0

Ou

e - 20 t = 0

Repare que a exponencial acima só é zero quando t tende a infinito. Logo, ficamos com a primeira possibilidade. Portanto, temos de resolver:

5 cos ⁡ 40 t + 5 2 s e n 40 t = 0

Que é o mesmo que:

5 cos ⁡ 40 t = - 5 2 s e n 40 t

Ajeitando:

t g 40 t = - 2

Ou ainda:

a r c t g t g 40 t = a r c t g - 2

40 t = a r c t g - 2

Com a ajuda de uma calculadora, verificamos que:

40 t = a r c t g - 2 = - 1,1071 + k π ,   c o m   k = … , - 1,0 , 1

Como queremos a primeira vez, temos de escolher o menor valor para t , e consequentemente para k , desde que t > 0 . Portanto, temos k = 1 . Então temos:

40 t = π - 1,1071

Calculando, encontramos:

t = 0,0509   s e g u n d o s

Resposta

A carga no capacitor no instante 0,01 segundo é q 0,01 = 4,5676   c o u l u m b s

O primeiro instante no qual a carga do capacitor é zero:

t = 0,0509   s e g u n d o s

Exercício Resolvido #4

Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON, 2001, pp. 264 - 12

Encontre a corrente estacionária em um circuito em série R-L-C quando L = 1 2 h e n r y , R = 20   o h m s , C = 0,001   f a r a d e E t = 100 s e n 60 t + 200 cos ⁡ 40 t .

Passo 1

Vimos na teoria que, pela lei de Kirchhoff das tensões, o circuito RLC se reduz a EDO de 2° ordem:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

Passo 2

Agora, vamos substituir os valores dados:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

0,5 d 2 q d t 2 + 20 d q d t + 1 0,001 q = 100 s e n 60 t + 200 cos ⁡ 40 t

Passo 3

Para resolver essa EDO, temos de resolver a parte homogênea associada e a não homogênea. Ou seja, a solução será:

q = q h + q p

A equação homogênea associada é :

0,5 d 2 q d t 2 + 20 d q d t + 1 0,001 q = 0

A equação auxiliar é:

0,5 r 2 + 20 r + 1000 = 0

Calculando ∆ temos:

∆ = 20 2 - 4 0,5 1000 = - 1600

Portanto as raízes são:

r 1 = - 20 + 40 i 1 = - 20 + 40 i

r 2 = - 20 - 40 i 1 = - 20 - 40 i

A solução da EDO homogênea associada é da forma:

q h = e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t

Pois estamos no caso em que ∆ < 0

Passo 4

Agora vamos encontrar a solução da parte não homogênea. Pelo método dos coeficientes a determinar, temos que o lado direito é composto de soma de trigonométricas, logo o nosso palpite será:

q p = A s e n 60 t + B cos ⁡ 60 t + C s e n 40 t + D c o s 40 t

Passo 5

A gente verifica que essas funções não estão presentes na solução homogênea. Veja que na homogênea, todas as funções trigonométricas são multiplicadas por e - 20 t o que não ocorre no nosso palpite.

Passo 6

Encontrando as derivadas temos:

d q d t = 60 A c o s 60 t - 60 B sen ⁡ 60 t + 40 C c o s 40 t - 40 D s e n 40 t

d 2 q d t 2 = - 3600 A s e n 60 t - 3600 B cos ⁡ 60 t - 1600 C s e n 40 t - 1600 D c o s 40 t

Passo 7

Substituindo na EDO temos:

0,5 d 2 q d t 2 + 20 d q d t + 1 0,001 q = 100 s e n 60 t + 200 cos ⁡ 40 t

- 1800 A s e n 60 t - 1800 B cos ⁡ 60 t - 800 C s e n 40 t - 800 D c o s 40 t +   1200 A c o s 60 t - 1200 B sen ⁡ 60 t + 800 C c o s 40 t - 800 D s e n 40 t + 1000 A s e n 60 t + 1000 B cos ⁡ 60 t + 1000 C s e n 40 t + 1000 D c o s 40 t = 100 s e n 60 t + 200 cos ⁡ 40 t

Ajeitando essa parada, temos:

s e n 60 t - 800 A - 1200 B + cos ⁡ 60 t 1200 A - 800 B + s e n 40 t 200 C - 800 D + cos ⁡ 40 t 200 D + 800 C = 100 s e n 60 t + 200 cos ⁡ 40 t

Temos então as seguintes equações:

- 800 A - 1200 B = 100

1200 A - 800 B = 0

200 C - 800 D = 0

200 D + 800 C = 200

Da segunda equação:

B = 3 2 A

Substituindo na primeira equação:

- 800 A - 1800 A = 100

Então:

A = - 1 26

E:

B = - 3 52

Da terceira equação:

C = 4 D

Substituindo na quarta equação:

200 D + 3200 D = 200

Então:

D = 1 17

E:

C = 4 17

Portanto a solução particular fica:

q p = - 1 26 s e n 60 t - 3 52 cos ⁡ 60 t + 4 17 s e n 40 t + 1 17 c o s 40 t

Passo 8

Logo, a solução geral é:

q t = e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t - 1 26 s e n 60 t - 3 52 cos ⁡ 60 t + 4 17 s e n 40 t + 1 17 c o s 40 t

Passo 9

Falta encontrar:

i = d q d t

Derivando:

i = - 20 e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t + e - 20 t - 40 c 1 sen ⁡ 40 t + 40 c 2 c o s 40 t - 30 13 cos ⁡ 60 t + 45 13 s e n 60 t + 160 17 cos ⁡ 40 t - 40 17 s e n 40 t

Passo 10

Perceba que a questão pede a corrente estacionária, ou seja, a corrente quanto t tende a infinito. Note que os termos - 20 e - 20 t c 1 cos ⁡ 40 t + c 2 s e n 40 t + e - 20 t - 40 c 1 sen ⁡ 40 t + 40 c 2 c o s 40 t

Tendem a zero quando t tende a infinito, devido ao teorema do confronto.

Portanto a corrente estacionária é dada por:

i t = - 30 13 cos ⁡ 60 t + 45 13 s e n 60 t + 160 17 cos ⁡ 40 t - 40 17 s e n 40 t

Resposta

A corrente estacionária é dada por:

i t = - 30 13 cos ⁡ 60 t + 45 13 s e n 60 t + 160 17 cos ⁡ 40 t - 40 17 s e n 40 t

Exercício Resolvido #5

Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON, 2001, pp. 264 - 13

Encontre a carga no capacitor em um circuito R-L-C em série, quando L = 1 2 h e n r y , R = 10   o h m s , C = 0,01   f a r a d . E t = 150   v o l t s , q 0 = 1   c o u l u m b e i 0 = 0   a m p e r e . Qual é a carga no capacitor após um longo período de tempo?

Passo 1

Vimos na teoria que, pela lei de Kirchhoff das tensões, o circuito RLC se reduz a EDO de 2° ordem:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

Passo 2

Agora, vamos substituir os valores dados:

L d 2 q d t 2 + R d q d t + 1 C q = E ( t )

0,5 d 2 q d t 2 + 10 d q d t + 1 0,01 q = 150

Passo 3

Para resolver essa EDO, temos de resolver a parte homogênea associada e a não homogênea. Ou seja, a solução será:

q = q h + q p

A equação homogênea associada é :

0,5 d 2 q d t 2 + 10 d q d t + 1 0,01 q = 0

A equação auxiliar é:

0,5 r 2 + 10 r + 100 = 0

Calculando ∆ temos:

∆ = 10 2 - 4 0,5 100 = - 100

Portanto as raízes são:

r 1 = - 10 + 10 i 1 = - 10 + 10 i

r 2 = - 10 - 10 i 1 = - 10 - 10 i

A solução da EDO homogênea associada é da forma:

q t = e - 10 t c 1 cos ⁡ 10 t + c 2 s e n 10 t

Pois estamos no caso em que ∆ < 0

Passo 4

Agora vamos encontrar a solução da parte não homogênea. Pelo método dos coeficientes a determinar, o nosso palpite será:

q p = A

Encontrando as derivadas temos:

d q d t = 0

d 2 q d t 2 = 0

Substituindo na EDO temos:

0,5 d 2 q d t 2 + 10 d q d t + 1 0,01 q = 150

0,5 . 0 + 10 . 0 + 1 0,01 A = 150

Então:

A = 3 2

Portanto a solução particular fica:

q p = 3 2

Passo 5

Logo, a solução geral é:

q t = e - 10 t c 1 cos ⁡ 10 t + c 2 s e n 10 t + 3 / 2  

Passo 6

Vamos usar as informações:

q 0 = 1

i ( 0 ) = 0

Primeiro vamos encontrar:

i = d q d t

Então temos:

q t = e - 10 t c 1 cos ⁡ 10 t + c 2 s e n 10 t + 3 / 2  

Derivando:

i = - 10 e - 10 t c 1 cos ⁡ 10 t + c 2 s e n 10 t + e - 10 t - 10 c 1 sen ⁡ 10 t + 10 c 2 c o s 10 t

Usando a segunda informação temos:

i 0 = 0 = - 10 e 0 c 1 cos ⁡ 0 + c 2 s e n 0 + e - 0 - 10 c 1 sen ⁡ 0 + 10 c 2 c o s 0  

Que nos leva a :

0 = - 10 c 1 + 10 c 2

c 1 = c 2

Utilizando a primeira informação, q 0 = 1 temos:

q 0 = 1 = e 0 c 1 cos ⁡ 0 + c 2 s e n 0 + 3 / 2  

Que resulta em:

c 1 = - 1 2

Então:

c 2 = - 1 2

Portanto a solução geral fica:

q t = e - 10 t - 1 2 cos ⁡ 10 t - 1 2 s e n 10 t + 3 / 2  

Passo 7

O problema ainda pede a carga no capacitor após um longo período de tempo, ou seja, ele quer q t quando t tende a infinito.

q t = e - 10 t - 1 2 cos ⁡ 10 t - 1 2 s e n 10 t + 3 / 2  

Perceba que o termo   e - 10 t - 1 2 cos ⁡ 10 t - 1 2 s e n 10 t tende a zero quando t tende ao infinito, devido ao teorema do confronto. Logo a carga no capacitor após um longo período de tempo é 3 2   c o u l u m b

Resposta

A carga no capacitor é:

q t = e - 10 t - 1 2 cos ⁡ 10 t - 1 2 s e n 10 t + 3 / 2  

A carga no capacitor após um longo período de tempo é 3 2   c o u l u m b

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 4, determine ω 0 ,Reδ , de modo a escrever a expressão dada na forma s = R ⋅ cos ⁡ ω 0 t - δ . s = 3 cos ⁡ 2 t + 4 sin ⁡ 2 t
Em cada um dos problemas de 1 a 4, determine ω 0 ,Reδ , de modo a escrever a expressão dada na forma s = R ⋅ cos ⁡ ω 0 t - δ . s = - cos ⁡ t + 3 sin ⁡ t
Um circuito em série te um capacitor de 10 - 3 F , um resistor de 3 × 10 2 Ω e um indutor de 0,2 H . A carga inicial do capacitor é 10 - 6 C e não há corrente incial. Encontre a carga Q no capacitor e
Um circuito um série tem um capacitor de 0,25 × 10 - 6 F e um indutor de 1 H . Se a carga inicial no campacitor for de 10 - 6 C e se não houver corrente inicial, encontre a carga Q no capacitor em qua
Em casa um dos problemas de 1 a 4, determine ω 0 , R e δ , de modo a escrever a expressão dada na forma s = R cos ⁡ ω 0 t - δ . s = 4 cos ⁡ 3 t - 2s e n3 t