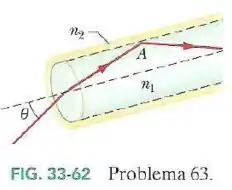
A Fig.33-62 mostra uma fibra ótica simplificada: um núcleo de plástico () envolvido por um revestimento de plástico com um índice de refração menor ().
Um raio luminoso incide em uma das extremidades da fibra com um ângulo . O raio deve sofrer reflexão interna total no ponto , onde atinge a interface núcleo-revestimento.
(Isso é necessário para que não haja perda de luz cada vez que o raio incide na interface.)
Qual é o maior valor de para o qual existe reflexão interna total no ponto ?
Passo 1
O ângulo de refração do feixe no núcleo de plástico da fibra ótica será:
Lembrando que o índice de refração do ar é :
Passo 2
Quando a luz que se propaga no núcleo de plástico e atinge a interface com o revestimento, ela sofre reflexão interna total.
O maior ângulo de incidência para o qual isso ocorre corresponde a um ângulo de refração de . Ou seja:
Substituindo os valores dados no enunciado:
Passo 3
Agora vamos conectar os dois passos dados.
Para isso, precisamos fazer uma construção geométrica. Vamos ver lateralmente o raio saindo do ar, incidindo no núcleo de plástico e depois no revestimento:
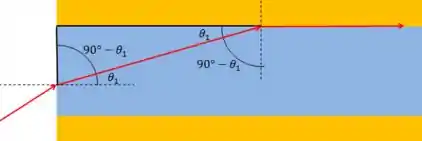
Podemos formar um triângulo retângulo entre o ponto que o raio de luz entra e o ponto que ele sofre reflexão total.
Por isso o ângulo de incidência vai ser . Rearrumando:
Substituindo na nossa primeira equação: