Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Pauli

Ver Teoria
Exercício 8123456791011

Enunciado

Quantos elétrons podem ter os seguintes números quânticos:

  1. n = 2 ,     l = 1
  2. n = 4 ,     l = 2 ,     m l = - 2
  3. n = 2
  4. n = 3 ,     l = 2 ,     m l = + 1

Passo 1

Pra resolver esse exercício, vamos fazer umas contas bem básicas e desenhar os diagramas das caixinhas pra “enxergar” melhor o nosso resultado.

Lembrando que:

  • O número de orbitais em cada subcamada é dado por 2 l + 1 .
  • Cada orbital comporta, no máximo, 2 elétrons.

Então o número máximo de elétrons na subcamada é 2 ( 2 l + 1 ) .

Vamos ver juntos cada caso.

Passo 2

  1. n = 2 ,     l = 1

    2. Com l = 1 a gente tem orbitais do tipo p.

    Pra saber a quantidade de orbitais 2p que temos: 2 l + 1 = 2.1 + 1 = 3 orbitais

    O que significa três “caixinhas”. E dentro de cada caixinha/orbital, podemos colocar 2 elétrons

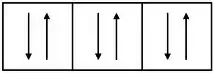
    Todos os elétrons que a gente representou aí tem n = 2 e l = 1 . Eles se diferenciam, portanto, pelos valores de m l e m s .

    Então 6 elétrons podem ter n = 2 e l = 1 .

    Passo 3

  2. n = 4 ,     l = 2 ,     m l = - 2

    3. Sabemos que dois elétrons não podem ter os 4 números quânticos em comum.

    O enunciado já determina 3 números quânticos, faltando apenas o m s , que pode assumir somente 2 valores: - 1 2   o u + 1 2 .

    Logo, apenas dois elétrons podem ter esses 3 números quânticos definidos. O elétron de spin ↑ e o elétron de spin ↓ .

    Vamos ver nas caixinhas:

    Orbitais com l = 2 são do tipo d. Para saber quantos orbitais do tipo d a gente tem:

    2 l + 1 = 2.2 + 1 = 5 orbitais.

    Cada caixinha/orbital representa um valor diferente de m l . Então nosso diagram fica assim:

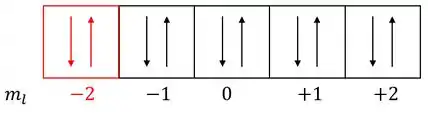
    E os 2 elétrons que podem ter os 3 números quânticos definidos no enunciado estão destacados em vermelho.

    Passo 4

  3. n = 2

    4. Aqui a gente tá falando de toda a segunda camada.

    As subcamadas possíveis para uma camada são dadas por:

    l = 0 ,   1 ,   … ,   n - 1

    Ou seja, o máximo valor que l pode assumir dentro de uma camada n é n - 1 .

    Pra n = 2 , os valores possíveis de l são:

    l = 0 ,   1

    Então a segunda camada da eletrosfera pode ter subníveis do tipo s e do tipo p.

    Para o subnível 2s, o número de orbitais é: 2 l + 1 = 2.0 + 1 = 1 orbital.

    Para o subnível 2p, o número de orbitais é: 2 l + 1 = 2.1 + 1 = 3 orbitais.

    Então para n = 2 a gente tem 4 orbitais. Com 2 elétrons possíveis por orbital, a gente vai ter 8 elétrons no nível n = 2 .

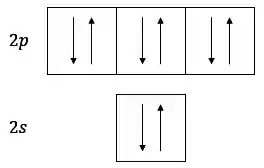
    Passo 5

  4. n = 3 ,     l = 2 ,     m l = + 1

Mesma situação do item b, onde a gente já tem 3 números quânticos definidos, o que significa que estamos falando de um único orbital, no qual só cabem 2 elétrons, com spin opostos.

Vamos ver..

2 l + 1 = 5 orbitais

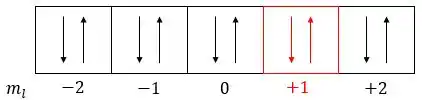
Resposta

  1. 6 elétrons
  2. 2 elétrons
  3. 8 elétrons
  4. 2 elétrons

Exercícios de Livros Relacionados

As seguintes configurações de camada de valência são possíveis para um átomo neutro. Que elemento e que configuração correspondem ao estado fundamental?
Para cada um dos seguintes átomos no estado fundamental, prediga o tipo de orbital (por exemplo, 1s, 2p, 3d, 4f, etc.) do qual um elétron poderia ser removido para torná-lo um íon +1:(a) Ge; (b) Mn; (
24. Use as configurações eletrônicas para sugerir uma razão por que ferro(II) é facilmente preparado a partir do ferro(II), mas a conversão do níquel(II) e cobalto(II) a níquel(III) e cobalto(III) são
O estado fundamental do O 2 possui dois elétrons π * desemparelhados com spins paralelos. Existem dois estados excitados de baixa energia. O estado A tem os dois elétrons π *com os spins antiparalelos
23. Use as configurações eletrônicas para explicar por que o ouro e a prata são mais reativos do que o cobre.