Cálculo de Probabilidades - Permutação
Produzido por Jorge Alberto NascimentoTeoria
Permutação
Imagina que compramos 5 livros (A, B, C, D, E) e queremos organizá-los em uma prateleira. Podemos organizar:
Percebe que existem diferentes maneiras de organizá-los? E se eu quiser contar de quantas maneiras eu posso organizar/ordenar esses livros. Como faremos? Vamos tentar pensar num jeito de calcular isso!
Vamos começar representando as cinco posições disponíveis desse modo:
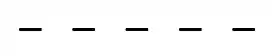
Pra começar a ordenar os livros, tenho que começar escolhendo um deles certo? Tenho exatamente, 5 opções de livros para escolher colocar primeiro na estante, então:
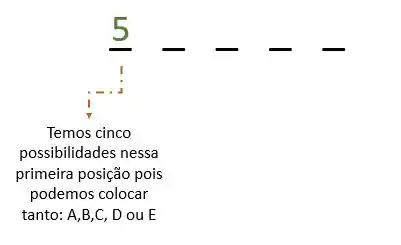
Agora, imaginem que escolhi um dos livros e ele já ocupa a primeira posição. O próximo passo é colocar um dos quatro livros restantes certo? Então temos 4 possibilidades para ocupar o segundo espaço da estante:
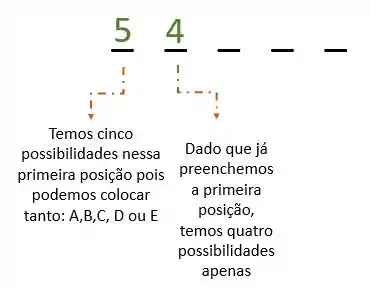
Ok, agora segundo o mesmo raciocínio, falta escolher um dos três livros restantes para o terceiro espaço da estante:
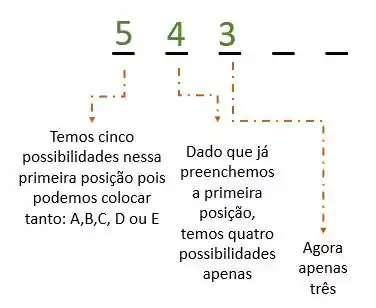
E fazemos assim até todos os espaços da estante sejam preenchidos:
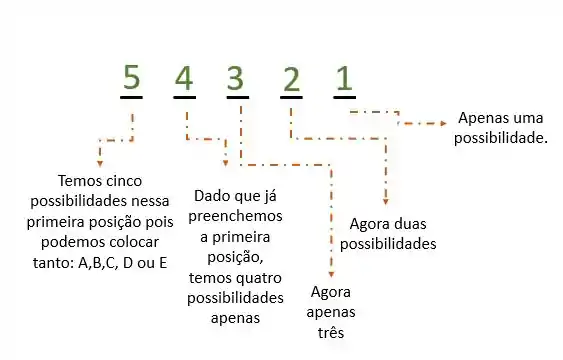
Ok, e agora o que faremos?
Percebe que para cada possibilidade de escolha, existem mais caminhos atrelados a ele? Por exemplo, imaginem que na primeira opção escolhemos o livro B. Para escolher o próximo livro temos 4 opções: A,C,D e E, ou seja, teríamos algo desse tipo:

Para estabelecer uma ordem de livros, cada escolha que fazemos gera varias possibilidades de ordens diferentes. Para contabilizar todos precisamos multiplicar cada escolha pelo número de possibilidades, ou seja, utilizaremos o chamado PRINCÍPIO MULTIPLICATIVO!
Pelo princípio multiplicativo, para descobrir a quantidade de ordens possíveis temos que:
Ou seja, temos 120 formas de organizar esses livros.
Isso que acabamos de realizar é chamado PERMUTAÇÃO.

Quando queremos descobrir de quantas maneiras podemos ordenar objetos distintos, na verdade, estamos permutando objetos.
Para um caso geral, com livros, podemos falar que:
Vamos para mais alguns exemplos?
Exemplo 1
Vamos calcular um Anagrama (muito comum em problemas de análise combinatória).
De quantas formas podemos ordenar as letras da palavra AMOR?
Temos 4 letras na palavra (A,M,O,R), e queremos calcular todos os anagramas dela. Nada mais do que um caso de permutação,
Esses são todos os anagramas da palavra amor:

Beleza?!
Permutação com Repetição
Vamos estudar agora outro caso de Análise Combinatória!
Imagine outra situação:
Ainda temos cinco livros para organizar na prateleira. Porém, dessa vez há dois livros iguais, ou seja, o mesmo título, por exemplo: A,A, B, C e D. Queremos descobrir quantas maneiras podemos organizar os livros sem repetir nenhuma ordem. Como seria?
Podemos imaginar várias possibilidades
A princípio, parece que precisamos resolver por permutação, pois continuamos com 5 livros e queremos ordená-los. Mas problema aqui é que há dois livros iguais…
Imagina o seguinte, vamos chamar os livros iguais de .
Quando permutamos todos esses cinco elementos (, B, C e D), duas das possíveis ordens são:
Percebem que como representam o mesmo livro, acabamos que contamos essa ordem duas vezes? Resolver esse problema é simples! Basta dividir o número de casos da permutação pelo número de casos repetidos.
Teremos assim:
Tranquilo?
Tá, mas e se fossem TRÊS livros idênticos? Imagina que temos 3 livros iguais: . É só calcular a permutação desses elementos e dividir por três de novo? NÃÃO!!!!

Calmaaaa meu pupilo!! Se liga no raciocínio:
No caso de dois livros iguais nos dividimos por dois porque só há duas maneiras de organizar dois elementos, nesse caso .
Mas se olharmos pra temos mais possibilidades :
Ou seja, quando calculamos a permutação acabamos repetindo o mesmo caso 6 vezes:
Olhando com mais atenção, para definirmos os casos de repetição entre acabamos permutando os tres elementos repetidos:
Então, para resolver o problema e descobrir de quantas formas podemos organizar os cinco livros, temos que dividir pela permutação dos 3 livros repetidos , para tirar a repetição:
O que fizemos foi a PERMUTAÇÃO COM REPETIÇÃO.

Ou seja, o que fizemos foi uma permutação, só que quando temos objetos repetidos nós “tiramos” (esse “tirar” é realizado com a divisão) esses objetos que se repetem. Pegou a ideia?
Para um caso genérico, sempre que queremos calcular o número de maneiras possíveis de ordenar com livros sendo alguns deles repetido vezes vamos ter:
Obs.: Se você reparar, fizemos a mesma coisa para o caso com duas repetições porque .
Vamos fazer mais alguns exemplos?
Exemplo 3
Como ficaria o anagrama de MISSISSIPI?
Nesse caso temos dois elementos repetidos, o “I” e o “S” que se repetem 4 vezes. Para calcular basta dividir a permutação de todos os elementos por duas vezes.
Show de bola?!?!
E como juntamos tudo isso que estamos vendo com o Cálculo de Probabilidades?
O cálculo da permutação que estamos vendo aqui é para saber a quantidade de eventos possíveis de um espaço amostral. Dessa forma, se tivermos algum caso de Cálculo de Probabilidades com Permutação, basta utilizar a fórmula abaixo:
Onde o numerador é a quantidade de eventos possíveis (as permutações) e o denominador o espaço amostral. Show de bola?!
Permutação Circular
Mais um caso de Permutação! Dessa vez vamos falar da PERMUTAÇÃO CIRCULAR.
Como o nome mesmo já diz, se trata de quantas maneira podemos distribuir os objetos ao redor de um círculo.
Imaginem a situação:
Alice, Beatriz, Camila, Duda e Estela vão jantar em uma mesa circular. De quantas maneiras podemos distribuir elas? Parece novamente um problema de permutação não é? Temos cinco elementos e queremos saber de quantas formas podemos ordená-los. Mas se liga só:
Observe algumas das formas possíveis de ordená-las:

Em todos esses casos, a Alice está entre a estela e a Beatriz, a Duda está entre a Estela e a Camila e assim por diante. A posição das meninas não mudou entre elas, justamente porque todas essas disposições se trata da mesma forma de ordenar as garotas, é como se girarmos o círculo sem de fato mudar a ordem das meninas.

Desse jeito descobrimos que há uma repetição, cada disposição das meninas se repete cinco vezes por que tem 5 lugares disponíveis, então para calcularmos o número de maneiras possíveis precisamos dividir a permutação dos cinco elementos por 5:
Vamos ver o caso geral!
Sempre que queremos calcular o número de maneiras possíveis de ordenar com n elementos em um círculo vamos ter:
Mas, note que:
Prontinho! Para facilitar dizemos que:
Beleza?! Vamos praticar!!
Exemplo 1
Permutação com Repetição
Exemplo 3
Permutação Circular
Exercícios Resolvidos
Exercício Resolvido #1
IME – Lista de Exercícios I – Professores Aderson Passos, Paulo Henrique Maranhão e Luis Antônio Seabra – Questão 02
Um inspetor visita 6 máquinas diferentes durante um dia. A fim de evitar que os operários saibam quando ele os irá inspecionar, o inspetor varia a ordenação de suas visitas. De quantas maneiras isso poderá ser feito?
Passo 1
Falou em variar a ordenação, falou em permutação!
Como vimos na teoria, a permutação não é nada mais do que uma forma de calcular de quantas formas possíveis e distintas eu posso ordenar uma série de coisas. Então vamos lá:
São 6 máquinas para inspecionar
Resposta
720
Exercício Resolvido #2
Escola Naval – 2000 – Questão 29
Um aspirante ganhou, em uma competição na Escola Naval, quatro livros diferentes de Matemática, três livros diferentes de Física e dois livros diferentes de Português. Querendo manter juntos aqueles da mesma disciplina, concluiu que poderia enfileirá-los numa prateleira de sua estante, de diversos modos. A quantidade de modos com que poderá fazê-lo é:
a)48
b) 72
c)192
d) 864
e) 1728
Passo 1
Primeira coisa: Vamos anotar os dados do enunciado!
- 4 livros de Matemática (distintos)
- 3 livros de Física (distintos)
- 2 livros de Português (distintos)
Uma observação importante é se atentar ao fato deles serem distintos, apesar de serem a mesma matéria, ou seja, a ordem entre eles importa.
Tá, agora que já notamos que teremos que ordenar entre os próprios livros de matemática, será que falta alguma coisa? SIM! Nós podemos mudar a ordem das matérias, ou seja, colocar matemática na frente da física, ou português na frente de todos.
Já percebeu que iremos dividir esse problema em dois certo?
Passo 2
(i) Ordenação das matérias
Temos três matéria: Matemática (M), Português (P) e Física (F) e para ordená-las, basta fazer a permutação entre elas:
Passo 3
(i) Ordenação dos livros das matérias
- Matemática ( 4 livros)
Para ordená-los, basta fazer: possibilidades
- Física (3 livros)
Faremos
- Português (2 livros)
Faremos:
E agora? O que faremos com esses casos? Somamos ou multiplicamos?
Lembre-se: iremos multiplicar! Para cada ordenação nas disciplinas, teremos essas ordenações dentro delas, portanto, utilizaremos o princípio multiplicativo!
Assim:
Resposta
Letra E
Exercício Resolvido #3
Gelson Iezzi, Osvaldo Dolce, David Degenszajn e Roberto Périgo, Matemática, 2ª ed
De um baralho de 52 cartas extraímos quatro simultaneamente.
a) Quantas são as possibilidades de sorteio das cartas?
b) Quantos resultados apresentam, entre as cartas sorteadas, o rei de espadas?
c) Quantos resultados apresentam exatamente dois ases?
Passo 1
Em um baralho de 52 cartas extraímos quatro simultaneamente, ou seja, a ordem não importa! Quando a ordem nãi importa em geral usamos Combinação.
Passo 2
a) Ele quer saber quantas são as POSSIBILIDADES e não as PROBABILIDADES. Olharemos apenas para o evento.
Evento A: Sorteio de 4 cartas de um baralho de um total de 52.
De quantas formas podemos retirar 4 cartas de um baralho de 52? Essa é exatamente a pergunta respondida pela fórmula da combinação! Nesse caso, :
Passo 3
b) Quantos resultados apresentam, entre as cartas sorteadas, o rei de espadas?
Olhando novamente para o nosso evento:
Evento B: Entre as quatro cartas sorteadas queremos ter o Rei de Espadas.
Neste caso temos que uma das quatro cartas já está definida (Rei de Espadas), enquanto as outras 3 não estão. Temos que sortear essas outras 3, de um total agora de 51 cartas!. Então o resultado será
Ou seja, temos 20.825 possíveis resultados, onde ao retiramos 4 cartas do baralho, uma delas seja um Rei de Espadas.
Passo 4
c) Quantos resultados apresentam exatamente dois ases?
Em um baralho temos 4 ases. Nesse caso queremos resultados com exatamente dois ases. Ou seja, a primeira coisa que devemos fazer é escolher dentre os quatro quais dois irão aparecer. Precisamos saber de quantas formas isso pode acontecer, que é exatamente a combinação :
Agora que já escolhemos quais as irão compor nossa retirada vamos pensar nas outras cartas.
O nosso baralho não tem agora 52 cartas. Temos que descontar os ases, portanto teremos 48 cartas. Ué, mas por que estamos descontando 4 ases?!
Descontamos os 4 ases pois queremos APENAS dois na nossa retirada, então temos 2 já sendo utilizados e os dois restantes NÃO PODEM SER possibilidades de retirada, senão, poderíamos vir a ter mais de exatamente dois ases, e não é isso que a questão quer!
Teremos assim, uma combinação de 2 cartas, entre 48 cartas totais (que com certeza não são ases, pois descontamos todos eles):
Finalmente, multiplicamos os resultados para ter o total (porque estamos primeiro selecionando os ases, e depois de selecionados, a gente selecionou o resto das cartas princípio multiplicativo)
Resposta
Exercício Resolvido #4
UFF-P1B-2013.1.-3
Uma bolsa tem bolas de borracha, bolas de plástico e bolas de vidro. Através de um sorteio aleatório, retira-se bolas da bolsa, sem reposição. Qual a probabilidade de se obter bolas de cada tipo, em qualquer ordem?
Passo 1
Primeiro vamos calcular a probabilidade de retirarmos bolas de cada tipo, pra isso basta considerar que como não temos reposição, o número de bolas dentro da bolsa vai diminuindo. O denominador vai diminuindo.
Passo 2
Agora vamos pensar na questão de poder ser em qualquer ordem, a ordem que eu calculei antes foi por exemplo:
de borracha, depois de plástico e no final de vidro.
Mas, poderíamos ter por exemplo:
Muitas possibilidades...
Bom, se a gente pensar nesse como sendo um anagrama.. podemos saber de quantas maneiras podemos bagunçar essas letras, lembrando de levar em consideração que temos letras repetidas que não devem contar como sendo duas situações diferentes.
Considerando como anagrama, teríamos:
Passo 3
Pra saber a probabilidade total então, é só a gente multiplicar a probabilidade que a gente calculou no início pra uma situação pelo , que simboliza a quantidade de situações possíveis.
Resposta
Exercício Resolvido #5
UERJ-L1-PROF FABIANO-11
Urna contem 5 bolas brancas, 4 vermelhas e 3 azuis. Extraem-se simultaneamente 3 bolas. Achar a probabilidade de:
- Nenhuma bola ser vermelha;
- Todas sejam da mesma cor.
Passo 1
Vamos usar o conceito básico de probabilidade.
Passo 2
Primeiro vamos pensar na quantidade de resultados possíveis na retirada de três bolas simultâneas.
Como a gente tem 12 bolas...
A gente vai ter possibilidades para as 3 bolas.
Opa, pera aí! As bolas não estão sendo retiradas simultaneamente? Isso quer dizer que a ordem não importa né? Ou melhor, nem tem ordem porque todas as três são retiradas ao mesmo tempo haha. Isso nos dá uma combinação de 3 em 12:
Passo 3
Pra que não saia nenhuma vermelha, a gente não conta as vermelhas. Ficariam então 8 bolas. Logo, uma combinação de 3 em 8!
A probabilidade que a gente quer seria então de:
Passo 4
(b)
Pra que todas sejam da mesma cor, a gente tem 3 situações:
: 3 bolas azuis. Combinação de 3 em 3:
3 bolas vermelhas. Combinação de 3 em 4:
3 bolas brancas. Combinação de 3 em 5:
Passo 5
A probabilidade total das bolas serem da mesma cor é o somatório das três situações calculadas.
Resposta
Exercício Resolvido #6
IME – Lista de Exercícios I – Professores Aderson Passos, Paulo Henrique Maranhão e Luis Antônio Seabra – Questão 19
Um banco possui um cofre que possui uma tranca com combinação. A tranca requer oito diferentes inteiros entre 1 e 90, que devem ser colocados em qualquer ordem. Entretanto, a tranca permite que 10 inteiros diferentes variando entre 1 e 90 sejam utilizados como uma combinação ou seja, a tranca abrirá se 8 dos 10 números da combinação forem colocados. Encontre a probabilidade de que um ladrão abra a porta na primeira tentativa.
Passo 1
Simbora interpretar o que ele disse?
Tá, ele falou que pra montar a senha desse cofre podemos escolher números de 1 até 90 (90 possibilidades) e que temos que escolher 8 números.
Então de 90 escolhemos 8 certo?
Essas são todas as possibilidades, ou seja, nosso espaço amostral :)
Passo 2
O enunciado diz também que se digitarmos 10 números e 8 desses forem a chave do cofre, conseguimos acessa-lo. Então de 10 números precisamos acertar apenas 8, ou seja, escolher 8.
Esse é o nosso evento certo?
Passo 3
Para saber a probabilidade de abrir de primeira o cofre faremos:
Beleza, agora vamos calcular esse valor lembrando da fórmula para a combinação!
Por fim, agora é só fazer a probabilidade.
Ou seja, mesmo com toda essa facilidade de poder escolher dez números, seria bem difícil esse ladrão conseguir abrir a tranca na primeira tentativa rs.
Resposta
Exercício Resolvido #7
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,110-11
Dentre seis números positivos e oito negativos, dois números são escolhidos ao acaso (sem reposição) e multiplicados. Qual a probabilidade de que o produto seja positivo?
Passo 1
Vamos lá... Primeira coisa: O que queremos?
Queremos selecionar dois números ao acaso e ter como produto desses números um número positivo.
Sabemos desde pequenos que:
Então queremos o primeiro e o terceiro caso certo?
Passo 2
Primeiro caso: ambos os números selecionados são positivos
Concordam que olhando para a multiplicação a ordem não altera? Afinal, a ordem dos fatores não altera o resultado né? Então usaremos combinação!
Evento A: Escolha de dois números positivos ENTRE os números positivos
Espaço Amostral: Dado todos os 14 números, escolher dois
Sabemos que
Passo 3
Segundo caso: ambos os números são negativos
Usaremos novamente combinação ;)
Evento B: Escolha de dois números negativos ENTRE os números negativos
Espaço Amostral: Dado todos os 14 números, escolher dois
Sabemos que
Para calcular a probabilidade de obter um resultado positivo, basta somar os casos:
Resposta
Exercício Resolvido #8
Lista RUMO AO ITA - FUNIVERSA – 2009-IPHAN-ANALISTA
Em um instituto de pesquisa trabalham, entre outros funcionários, 3 físicos, 6 biólogos e 2 matemáticos. Deseja-se formar uma equipe com 4 desses 11 estudiosos, para realizar uma pesquisa. Se essa equipe for composta escolhendo-se os pesquisadores de forma aleatória, a probabilidade de todos os físicos serem escolhidos é um número cujo valor está compreendido entre:
a)0,00 e 0,01
b)0,01 e 0,02
c)0,02 e 0,03
d)0,03 e 0,04
e) 0,04 e 0,05
Passo 1
Vamos usar a fórmula
Onde
número de casos favoráveis
número de casos possíveis
Passo 2
Vamos ver primeiro o número de casos possíveis:
Temos uma equipe de 11 estudiosos no total e queremos montar um grupo de quatro pessoas aleatoriamente, sem importar a ordem, certo? Então de 11 escolheremos 4.
Esse é o número de casos possíveis..
Passo 3
Agora vamos olhar para o número de casos favoráveis: todos os físicos na equipe.
Temos um total de 3 físicos e 8 de outras disciplinas. Como preciso na minha equipe de 4 pessoas, teremos:
- 3 físicos Escolher 3 físicos entre os 3 físicos
- 1 qualquer outra matéria Escolher uma pessoa dentre as 8 restantes
Agora basta multiplicar as duas (isso porque primeiro estamos escolhendo os físicos e depois o restante):
Passo 4
A probabilidade será dada por:
Resposta
Letra C
Exercício Resolvido #9
UFF-P1B-2013.1.-3
Uma bolsa tem bolas de borracha, bolas de plástico e bolas de vidro. Através de um sorteio aleatório, retira-se bolas da bolsa, sem reposição. Qual a probabilidade de se obter bolas de cada tipo, em qualquer ordem?
Passo 1
Primeiro vamos calcular a probabilidade de retirarmos bolas de cada tipo, pra isso basta considerar que como não temos reposição, o número de bolas dentro da bolsa vai diminuindo. O denominador vai diminuindo.
Passo 2
Agora vamos pensar na questão de poder ser em qualquer ordem, a ordem que eu calculei antes foi por exemplo:
de borracha, depois de plástico e no final de vidro.
Mas, poderíamos ter por exemplo:
Muitas possibilidades...
Bom, se a gente pensar nesse como sendo um anagrama.. podemos saber de quantas maneiras podemos bagunçar essas letras, lembrando de levar em consideração que temos letras repetidas que não devem contar como sendo duas situações diferentes.
Considerando como anagrama, teríamos:
Passo 3
Pra saber a probabilidade total então, é só a gente multiplicar a probabilidade que a gente calculou no início pra uma situação pelo , que simboliza a quantidade de situações possíveis.
Resposta
Exercício Resolvido #10
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,123-33
Um grupo de 12 homens e 8 mulheres concorre a três prêmios através de um sorteio sem reposição de seus nomes. Qual a probabilidade de:
a) nenhum homem ser sorteado?
b) um prêmio ser ganho por homem?
c) dois homens serem premiados?
Passo 1
Como estamos falando de um sorteio a ordem não importa, o que importa é ser sorteado, portanto usaremos Combinação
A) Evento A: Nenhum homem ser sorteado Serem sorteadas 3 mulheres
Espaço amostral: Escolher três pessoas aleatoriamente
Assim:
Passo 2
b) Evento B: Um prêmio ser ganho por um homem Duas mulheres ganham os outros:
1º) Escolha do homem (H)
2º) Escolha das duas mulheres (M)
Espaço amostral: Escolher três pessoas aleatoriamente
Portanto
Passo 3
c) Evento C: dois homens serem premiadosuma mulher ser premiada.
1º) Escolha do homem
2º) Escolha da mulher
Espaço amostral: Escolher três pessoas aleatoriamente
Portanto
Resposta
Exercício Resolvido #11
IME – Lista de Exercícios I – Professores Aderson Passos, Paulo Henrique Maranhão e Luis Antônio Seabra – Questão 05
Um jogador A lança seis dados e ganha caso consiga pelo menos um resultado igual a um. Um outro jogador B lança doze dados e ganha caso consiga pelo menos dois resultados iguais a um. Quem tem a maior probabiliade de ganhar?
Passo 1
Vamos olhar cada jogador separadamente ok?
Olha o jogador A:
Nº de dados: 6
Vitória: Pelo menos um resultado igual a 1
Isso significa que ele perde se não tiver nenhum resultado igual a 1 correto?
Então:
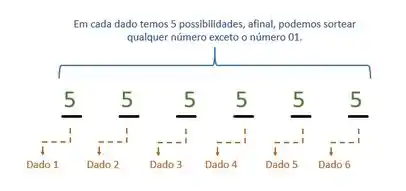
Então para cada dado temos que uma probabilidade de:
Para os seis dados teremos:
A probabilidade de vitória será:
Passo 2
Agora vamos olhar o jogador B:
Nº de dados: 12
Vitória: Pelo menos dois resultados iguais a 1.
Ou seja, ele perde se nenhum resultado for igual a 1 ou se apenas um resultado for igual a 1.
Seguindo a mesma linha de raciocínio do jogador A, teremos:
Passo 3
1ª caso: Nenhum resultado igual a 1.
Passo 4
2º caso: Apenas um resultado igual a 1.
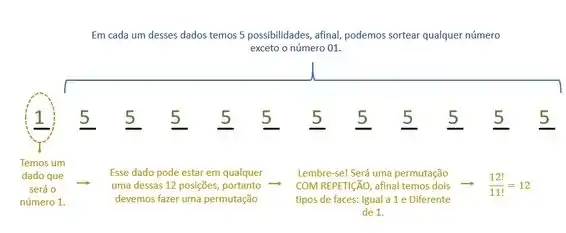
Então teremos:
Passo 5
Como dividimos em casos precisamos SOMAR as respostas:
Probabilidade de B NÃO ganhar:
Então a probabilidade dele ganhar é:
Passo 6
Comparando as probabilidades, quem tem a maior chance de ganhar é A.
Resposta
Jogador A
Exercício Resolvido #12
UERJ-L1-PROF FABIANO-11
Urna contem 5 bolas brancas, 4 vermelhas e 3 azuis. Extraem-se simultaneamente 3 bolas. Achar a probabilidade de:
- Nenhuma bola ser vermelha;
- Todas sejam da mesma cor.
Passo 1
Vamos usar o conceito básico de probabilidade.
Passo 2
Primeiro vamos pensar na quantidade de resultados possíveis na retirada de três bolas simultâneas.
Como a gente tem 12 bolas...
A gente vai ter possibilidades para as 3 bolas.
Opa, pera aí! As bolas não estão sendo retiradas simultaneamente? Isso quer dizer que a ordem não importa né? Ou melhor, nem tem ordem porque todas as três são retiradas ao mesmo tempo haha. Isso nos dá uma combinação de 3 em 12:
Passo 3
Pra que não saia nenhuma vermelha, a gente não conta as vermelhas. Ficariam então 8 bolas. Logo, uma combinação de 3 em 8!
A probabilidade que a gente quer seria então de:
Passo 4
(b)
Pra que todas sejam da mesma cor, a gente tem 3 situações:
: 3 bolas azuis. Combinação de 3 em 3:
3 bolas vermelhas. Combinação de 3 em 4:
3 bolas brancas. Combinação de 3 em 5:
Passo 5
A probabilidade total das bolas serem da mesma cor é o somatório das três situações calculadas.
Resposta
Exercício Resolvido #13
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 122- 29 (Adaptada).
Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma (sem reposição), até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Passo 1
Vamos lá!
Temos um total de 8 lâmpadas: 6 boas (L) e 2 queimadas ()
Essas lâmpadas foram misturadas e devemos testar uma a uma até encontrar as duas defeituosas, ou seja, podemos ter esses casos aqui ô:
1º caso: ou seja, de cara testamos as duas queimadas.
2º caso: testamos a primeira, está queimada, contudo a segundo está boa e a terceira está queimada.
E assim por diante certo?
Maas o enunciado pede a probabilidade de ocorrer um caso em particular, veja só:
Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma, até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Para resolver esse probleminha vamos usar a permutação com repetição.

Por quê?? Vamos ver agora!!!
Passo 2
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Note que neste caso, os primeiros três testes não estão determinados, contudo o último (o quarto) necessariamente precisa ser uma lâmpada queimada. Podemos dizer então que ela está fixa na quarta posição certo?

Percebemos então que se olharmos apenas para as três primeiras retiradas podemos fazer uma permutação entre essas lâmpadas:
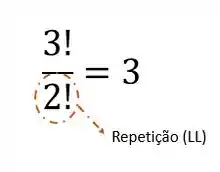
Então sabemos que seja lá qual for a probabilidade, precisaremos multiplicar por três, pois temos três possibilidades desse resultado acontecer.
Passo 3
Agora vamos calcular a probabilidade:
- Probabilidade da primeira lâmpada ser boa:
- Probabilidade da primeira lâmpada ser queimada:
- Probabilidade da segunda lâmpada ser boa, dado que a primeira foi boa:
Probabilidade da segunda lâmpada ser boa, dado que a primeira foi queimada:
Probabilidade da segunda lâmpada ser queimada, dado que a primeira foi boa:
E por ae vai, então percebemos que terá sempre essa cara:
Probabilidade de termos: 2 lâmpadas boas e 2 queimadas:
Probabilidade de na quarta retirada termos a última queimada:
Resposta
Exercício Resolvido #14
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,110-11
Dentre seis números positivos e oito negativos, dois números são escolhidos ao acaso (sem reposição) e multiplicados. Qual a probabilidade de que o produto seja positivo?
Passo 1
Vamos lá... Primeira coisa: O que queremos?
Queremos selecionar dois números ao acaso e ter como produto desses números um número positivo.
Sabemos desde pequenos que:
Então queremos o primeiro e o terceiro caso certo?
Passo 2
Primeiro caso: ambos os números selecionados são positivos
Concordam que olhando para a multiplicação a ordem não altera? Afinal, a ordem dos fatores não altera o resultado né? Então usaremos combinação!
Evento A: Escolha de dois números positivos ENTRE os números positivos
Espaço Amostral: Dado todos os 14 números, escolher dois
Sabemos que
Passo 3
Segundo caso: ambos os números são negativos
Usaremos novamente combinação ;)
Evento B: Escolha de dois números negativos ENTRE os números negativos
Espaço Amostral: Dado todos os 14 números, escolher dois
Sabemos que
Para calcular a probabilidade de obter um resultado positivo, basta somar os casos:
Resposta
Exercício Resolvido #15
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,123-33
Um grupo de 12 homens e 8 mulheres concorre a três prêmios através de um sorteio sem reposição de seus nomes. Qual a probabilidade de:
a) nenhum homem ser sorteado?
b) um prêmio ser ganho por homem?
c) dois homens serem premiados?
Passo 1
Como estamos falando de um sorteio a ordem não importa, o que importa é ser sorteado, portanto usaremos Combinação
A) Evento A: Nenhum homem ser sorteado Serem sorteadas 3 mulheres
Espaço amostral: Escolher três pessoas aleatoriamente
Assim:
Passo 2
b) Evento B: Um prêmio ser ganho por um homem Duas mulheres ganham os outros:
1º) Escolha do homem (H)
2º) Escolha das duas mulheres (M)
Espaço amostral: Escolher três pessoas aleatoriamente
Portanto
Passo 3
c) Evento C: dois homens serem premiadosuma mulher ser premiada.
1º) Escolha do homem
2º) Escolha da mulher
Espaço amostral: Escolher três pessoas aleatoriamente
Portanto
Resposta
Exercício Resolvido #16
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,123-38
Um fabricante afirma que apenas 5% de todas as válvulas que produz têm duração inferior a 20 horas. Uma indústria compra semanalmente um grande lote de válvulas desse fabricante, mas sob a seguinte condição: ela aceita o lote se, em dez válvulas escolhidas ao acaso, no máximo uma tiver duração inferior a 20 hora; caso contrário, o lote todo é rejeitado.
a) Se o fabricante de fato tem razão, qual a probabilidade de um lote ser rejeitado?
b) Suponha agora que o fabricante esteja mentindo, isto é, na verdade a proporção de válvulas com duração inferior a 20 horas é de 10%. Qual a probabilidade de um lote ser aceito, segundo o critério acima?
Passo 1
Vaaaamos lá?!
O fabricante diz que apenas 5% das válvulas tem duração inferior a 20 horas OU SEJA: A probabilidade de uma válvula durar menos de 20horas é Pensando no complementar podemos afirmar que a probabilidade de uma válvula durar mais de 20 horas
Queremos calcular a probabilidade de um lote ser rejeitado, certo?!
Temos que a probabilidade de um lote ser rejeitado é a probabilidade complementar dele ser aceito, ou seja
Então vamos calcular a probabilidade dele ser aceito, beleza?!

Ele diz que para uma indústria aceitar o lote devemos ter no máximo uma válvula com duração inferior a 20 horas, isto significa que:
- Podemos não ter nenhuma
- Podemos ter uma
Passo 2
Assim, vamos ter 2 eventos:
1º) Evento A: Não temos nenhuma válvula com duração inferior a 20 horas.
Passo 3
2º) Evento B: Apenas uma válvula com duração inferior a 20 horas.
Bom, como temos um total de 10 válvulas e apenas uma possui a duração abaixo do padrão, precisamos decidir qual delas será a válvula defeituosa:
Lembrando que o nosso evento aqui são os casos favoráveis, beleza?!
Agora calculamos a probabilidade disso ocorrer:
Passo 4
Assim podemos falar que:
Então a probabilidade do loter ser rejeitado:
Passo 5
b) Agora mudamos as probabilidades
- Válvula com duração inferior a 20 horas: 10%
- Válvula com duração superior a 20 horas: 90%
A probabilidade de ser aceito será a mesma expressão trocando apenas os valores:
Resposta
a) 0,086
b) 0,736
Exercício Resolvido #17
IME – Lista de Exercícios I – Professores Aderson Passos, Paulo Henrique Maranhão e Luis Antônio Seabra – Questão 05
Um jogador A lança seis dados e ganha caso consiga pelo menos um resultado igual a um. Um outro jogador B lança doze dados e ganha caso consiga pelo menos dois resultados iguais a um. Quem tem a maior probabiliade de ganhar?
Passo 1
Vamos olhar cada jogador separadamente ok?
Olha o jogador A:
Nº de dados: 6
Vitória: Pelo menos um resultado igual a 1
Isso significa que ele perde se não tiver nenhum resultado igual a 1 correto?
Então:
Então para cada dado temos que uma probabilidade de:
Para os seis dados teremos:
A probabilidade de vitória será:
Passo 2
Agora vamos olhar o jogador B:
Nº de dados: 12
Vitória: Pelo menos dois resultados iguais a 1.
Ou seja, ele perde se nenhum resultado for igual a 1 ou se apenas um resultado for igual a 1.
Seguindo a mesma linha de raciocínio do jogador A, teremos:
Passo 3
1ª caso: Nenhum resultado igual a 1.
Passo 4
2º caso: Apenas um resultado igual a 1.
Então teremos:
Passo 5
Como dividimos em casos precisamos SOMAR as respostas:
Probabilidade de B NÃO ganhar:
Então a probabilidade dele ganhar é:
Passo 6
Comparando as probabilidades, quem tem a maior chance de ganhar é A.
Resposta
Jogador A
Exercício Resolvido #18
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 122- 29 (Adaptada).
Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma (sem reposição), até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Passo 1
Vamos lá!
Temos um total de 8 lâmpadas: 6 boas (L) e 2 queimadas ()
Essas lâmpadas foram misturadas e devemos testar uma a uma até encontrar as duas defeituosas, ou seja, podemos ter esses casos aqui ô:
1º caso: ou seja, de cara testamos as duas queimadas.
2º caso: testamos a primeira, está queimada, contudo a segundo está boa e a terceira está queimada.
E assim por diante certo?
Maas o enunciado pede a probabilidade de ocorrer um caso em particular, veja só:
Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma, até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Passo 2
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Note que neste caso, os primeiros três testes não estão determinados, contudo o último (o quarto) necessariamente precisa ser uma lâmpada queimada. Podemos dizer então que ela está fixa na quarta posição certo?
Percebemos então que se olharmos apenas para as três primeiras retiradas podemos fazer uma permutação entre essas lâmpadas:
Então sabemos que seja lá qual for a probabilidade, precisaremos multiplicar por três, pois temos três possibilidades desse resultado acontecer.
Passo 3
Agora vamos calcular a probabilidade:
- Probabilidade da primeira lâmpada ser boa:
- Probabilidade da primeira lâmpada ser queimada:
- Probabilidade da segunda lâmpada ser boa, dado que a primeira foi boa:
Probabilidade da segunda lâmpada ser boa, dado que a primeira foi queimada:
Probabilidade da segunda lâmpada ser queimada, dado que a primeira foi boa:
E por ae vai, então percebemos que terá sempre essa cara:
Probabilidade de termos: 2 lâmpadas boas e 2 queimadas:
Probabilidade de na quarta retirada termos a última queimada:
Resposta
Exercício Resolvido #19
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,123-38
Um fabricante afirma que apenas 5% de todas as válvulas que produz têm duração inferior a 20 horas. Uma indústria compra semanalmente um grande lote de válvulas desse fabricante, mas sob a seguinte condição: ela aceita o lote se, em dez válvulas escolhidas ao acaso, no máximo uma tiver duração inferior a 20 hora; caso contrário, o lote todo é rejeitado.
a) Se o fabricante de fato tem razão, qual a probabilidade de um lote ser rejeitado?
b) Suponha agora que o fabricante esteja mentindo, isto é, na verdade a proporção de válvulas com duração inferior a 20 horas é de 10%. Qual a probabilidade de um lote ser aceito, segundo o critério acima?
Passo 1
Vaaaamos lá?
O fabricante diz que apenas 5% das válvulas tem duração inferior a 20 horas OU SEJA: A probabilidade de uma válvula durar menos de 20horas é 5% (=0,05). Pensando no complementar podemos afirmar que a probabilidade de uma válvula durar mais de 20 horas é 95% (=0,95). Certo?
Ele diz que para uma indústria aceitar o lote devemos ter no máximo uma válvula com duração inferior a 20 horas, isto significa que:
- Podemos não ter nenhuma
- Podemos ter uma
Concorda que a probailidade de um lote ser rejeitado é a probabilidade complementar dele ser aceito, ou seja
Então vamos calcular a probabilidade dele ser aceito...
Passo 2
1º) Evento A: Não temos nenhuma válvula com duração inferior a 20 horas.
Passo 3
2º) Evento B: Apenas uma válvula com duração inferior a 20 horas.
Bom, como temos um total de 10 válvulas e apenas uma possui a duração abaixo do padrão, precisamos decidir qual delas será a válvula defeituosa:
E calculamos a probabilidade disso ocorrer:
Passo 4
Assim podemos falar que:
Então a probabilidade do loter ser rejeitado:
Passo 5
b) Agora mudamos as probabilidades
- Válvula com duração inferior a 20 horas: 10%
- Válvula com duração superior a 20 horas: 90%
A probabilidade de ser aceito será a mesma expressão trocando apenas os valores:
Resposta
a) 0,086
b) 0,736