Eventos Independentes & Mutuamente Exclusivos
Teoria
Eventos Independentes
Fala Aíí!! Pensa comigo na seguinte situação: Imagine que uma moeda é lançada duas vezes. Aí eu vou e te pergunto qual a probabilidade de cair coroa no segundo lançamento? Você piraria??? Calmaaaa!!!!
Vamos tentar entender melhor a situação:
Vamos supor que você lance essa moeda uma vez, e tenha como resultado coroa. Se você lançar essa moeda novamente, após esse primeiro lançamento, essa coroa que você tirou no primeiro lançamento vai ter alguma influência sobre o próximo resultado? Não! É aqui que vai entrar os eventos independentes!!
Como o nome já diz, eventos independentes são aqueles que não dependem um do outro, ou seja, o fato de um deles acontecer não altera a probabilidade do outro ocorrer. Mas como calcular?
Voltando ao exemplo:
Vamos chamar nosso evento de evento A:
Temos as seguintes possibilidades:
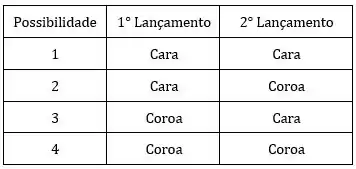
Ou seja, nosso espaço amostral é 4.
Queremos as possibilidades do segundo laçamento ser coroa, certo? Então, temos as seguintes opções:
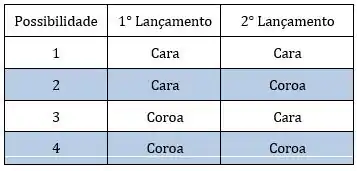
Ou seja, temos dois casos possíveis.
Vamos calcular P(A):
Essa foi fácil, né?
Humm.. mas como vamos saber se dois eventos são independentes ou não?
É exatamente isso que vamos descobrir agora. Vem comigo!
Se dois eventos são independentes, então:
Ou seja, a probabilidade do evento A e do evento B ocorrer é exatamente a probabilidade de A multiplicada pela probabilidade de B.
Por exemplo, vamos acrescentar um evento B no nosso primeiro exemplo:
Qual a probabilidade dos dois eventos ocorrerem?
Sabemos que o fato de um evento ocorrer não tem ligação com o outro, certo? Então, são eventos independentes e queremos calcular .
Vamos começar calculando :
Calculando :
Então:
Prontinho! Vamos verificar na tabela se isso é verdade?
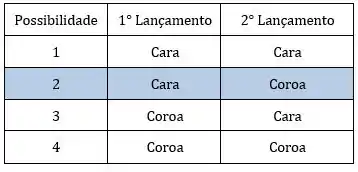
Show de bola?!
Eventos Mutuamente Exclusivos
Dizemos que dois eventos são mutuamente exclusivos quando eles são disjuntos, ou seja, quando não possuem interseção.
E tudo volta à Teoria dos Conjuntos...
Exemplo
Em um único lançamento de dado, qual a probabilidade de obter um número que seja par e ímpar ao mesmo tempo?
Deu ruim, né? Calma que já vai fazer sentido.
Vamos chamar os dois eventos do exemplo de A e B:
Queremos calcular a probabilidade dos dois eventos ocorrerem, ou seja, P
Mas ao lançar um dado é IMPOSSÍVEL obter um número par e ímpar ao mesmo tempo, certo?
Isso porque não existe interseção entre esses dois eventos, ou seja:
Quando isso acontece, dizemos que os eventos são mutuamente exclusivos!
Tá, mas o que isso quer dizer na prática?
Com isso podemos concluir outras coisas. Por exemplo, se queremos calcular a união de probabilidades temos a seguinte fórmula:
Se os eventos e são mutuamente exclusivos, logo , portanto:
Ou seja, a probabilidade da união de eventos mutuamente exclusivos é a soma das probabilidades de cada evento!
Além disso, quando dois eventos não tiverem interseção a probabilidade condicional também irá mudar. Vamos dar uma olhada na fórmula:
Como teremos:
Ou seja, quando falamos de eventos mutuamente exclusivos podemos afirmar que a probabilidade de B ocorrer tal que A ocorreu é ZERO.
Isso faz sentido no nosso exemplo, certo? Se quiséssemos calcular , estamos calculando a probabilidade do número do dado ser ímpar dado que o número do dado é par, e isso é impossível de acontecer, logo:
Importante!
Não podemos confundir eventos MUTUAMENTE EXCLUSIVOS com eventos INDEPENDENTES.
Eventos independentes são aqueles que:
Nada podemos afirmar sobre eles serem mutuamente exclusivos ou não. E vice versa!
Partiu exercício para fixar melhor esses paranauês todos aí!
Eventos Mutuamente Exclusivos
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,115-21
Na tabela abaixo, os números que aparecem são as probabilidades relacionadas com a ocorrência de etc. Assim , enquanto .
Verifique se A e B são independentes.
Passo 1
Vamos lá! O que significa dois eventos serem independentes? Te digo agora: Para serem considerados independentes, deve valer a seguinte igualdade:
Beleza?!
Precisamos encontrar então quem é e
Passo 2
Vamos analisar a tabela para encontrar os valores de e
Da mesma forma, a primeira coluna em P(B) e a segunda coluna em .
Temos então que
Se fizermos as continhas, teremos
Tá... mas eles serão independentes ou não?
Se você reparar, na tabela temos que . Ou seja, A e B não são independentes.
Beleza?!
Resposta
Não são independentes.
Exercício Resolvido #2
Marcos N. Magalhães e Antonio Carlos P. Lima, Noções de Probabilidade e Estatística, 6ªed. São Paulo: Edusp, 2004, 48-02
Se ; e , determine o valor de r no caso de:
(a) e serem mutuamente exclusivos.
Passo 1
(a)
Para eventos mutuamente exclusivos, a gente sabe que:
Então, substituindo os valores do problema:
Resposta
Exercício Resolvido #3
Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004, 49-03
Verifique se é válida a afirmação abaixo
Se então A e B não podem ser disjuntos.
Passo 1
Eventos disjuntos? O que é isso mesmo?
Disjuntos Interseção igual a zero Mutualmente Exclusivos
Se eles fossem disjuntos, teríamos que:
E assim
Certo?
Dessa forma se não podem ser disjuntos!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004, 48 - 01
Considere dois eventos A e B, mutuamente exclusivos, com P(A)=0,3 e P(B) =0,5. Calcule:
a)
b)
c)
d)
Passo 1
Mutuamente exclusivos Interseção igual a zero!
Assim,
Passo 2
b)
Sabemos que podemos escrever
Como
Passo 3
c)
Opa, o que significa mesmo? É o complementar de A, ou seja, tudo que pertence ao meu espaço amostral mas NÃO pertence a A.
Passo 4
d)
Seguindo a mesma linha de raciocínio da letra (c)
Resposta
a) 0
b) 0,8
c) 0,7
d) 0,2
Exercício Resolvido #5
UFRJ, ProbEst, P1/2012.2, 1
Para competir em uma certa regata as embarcações podem velejar com no máximo 4 tripulantes. Os tripulantes de cada embarcação são inscritos previamente e não podem ser alterados mais tarde. A embarcação Chez Moi, participante da regata, inscreveu Alberto, Bernardo, Carlos e Diogo. Carlos e Diogo confirmaram a presença na regata com probabilidade 100%. A probabilidade de Alberto comparecer à regata é 50%, enquanto que a de Bernardo, é 70%. A decisão de comparecer ou não por parte de Alberto não influencia a decisão de comparecer ou não por parte de Bernardo e vice versa. Note que o fato do número de velejadores no barco poder ser igual a 2, 3 ou 4 caracteriza uma partição do espaço amostral. Com a tripulação completa, a embarcação Chez Moi tem 80% de probabilidade de vencer a regata; com apenas Carlos e Diogo, esta probabilidade cai para 20%; e com três tripulantes a probabilidade de vencer é de 50%. Pede-se calcular a probabilidade de que:
- pelo menos um dos velejadores, Alberto ou Bernardo, compareçam à regata;
Passo 1
(a)
Vamos chamar de:
No exercício ele quer a probabilidade de ou .
A gente sabe que:
E que:
Passo 2
O exercício nos indica também que e são eventos independentes, então:
Com isso:
Substituindo os valores:
Resposta
Exercício Resolvido #6
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 115-19
As probabilidades de que dois eventos independentes ocorra são p e q, respectivamente. Qual a probabilidade:
a) de que nenhum desses eventos ocorra?
b) de que pelo menos um desses eventos ocorra?
Passo 1
Vamos começar dando nome aos bois...
Seja A o evento cujo P(A) = p e B o evento cujo P(B) = q.
Se o enunciado afirma que ele são independentes, concluímos que:
Passo 2
a) Qual a probabilidade de que nenhum desses eventos ocorra?
Vamos interpretar isso: A probabilidade de que nenhum ocorra é 1 – (probabilidade de pelo menos um ocorrer) certo?
E teremos por sua vez, a probabilidade de pelo menos um ocorrer é .
Mas quem é ?
Sabemos que: ou seja .
Substituindo teremos:
Então a probabilidade de que nenhum evento ocorra será:
Passo 3
b) Qual a probabilidade de que pelo menos um desses eventos ocorra
Essa probabilidade nós já calculamos na letra (a). É
Resposta
a)
b)
Exercício Resolvido #7
PUCRIO-P1-2015.1-1B
b) Considere a seguinte afirmação: Se e são dois eventos mutuamente exclusivos, então , indicando que a ocorrência do evento não traz informação sobre a probabilidade de ocorrência do evento . Esta afirmativa é verdadeira ou falsa?
Passo 1
Então, a gente até usou essa ideia no conteúdo pra simplificar. Mas isso confunde muito, dizer que dois eventos são mutuamente exclusivos não significa que eles são independentes, só significa que a interseção deles é vazia.
De acordo com o enunciado, usando a fórmula a probabilidade condicional, a gente teria:
Usando ...
Que é a ideia de eventos independentes. Ou seja, a afirmação está erraaada. Porque uma coisa não implica na outra.
Passo 2
Na realidade, ao dizer que os eventos são mutuamente exclusivos, a gente diz que a interseção deles é zero. Então:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 126-55
(a) Se A, B e C são independentes, prove que são independentes.
(b) Nas mesmas condições, prove que são independentes.
Passo 1
Vamos lá! O que significa dizer que A, B e C são independentes?
Quer dizer que
Pelas propriedades de conjuntos posso dizer que:
Assim,
Como B e C são independentes podemos falar que
Assim do lado esquerdo da igualdade teremos:
E do lado direito da igualdade teremos:
Assim concluímos que
Passo 2
Agora queremos mostrar que e C são independentes. Ou seja, queremos mostrar que:
Essa é a nossa hipótese
A ideia agora é desenvolver cada lado da igualdade separadamente e comparar as respostas. Se forem iguais nossa hipótese é verdadeira, se não é falsa. Ok?
Lado esquerdo:
1º passo: Vamos chamar ok?
2º passo: Sabemos que:
Substituindo teremos:
3º passo: Voltando com A e B na expressão teremos:
4º passo: Sabemos pelo 2º passo que podemos escrever de outra forma, assim
5º passo: Agora vamos olhar para o ... Lembra que podemos “abrir” ele?
6º passo: Substituindo tudo na expressão e fazendo as contas
Agora guarda esse resultado e vamos olhar pro lado direito da nossa igualdade!
Lado direito:
1º passo: Podemos “abrir” o né?
2º passo: Fazendo a distribuitiva teremos
Opa! Percebe que chegamos a um resultado igual ao anterior? Ou seja, o resultado o lado direito é IGUAL ao resultado do lado esquerdo, o que significa que a nossa hipótese é verdadeira!
Resposta
Ei, a resposta está no passo a passo :)