Teoria da Confiabilidade
Produzido por Jorge Alberto NascimentoTeoria
Introdução
Otimização. Eficiência. Certezas.
O que isso tudo tem a ver com probabilidade?
Bom, nos dias de hoje quanto mais certeza melhor correto? Você não vai querer fazer um investimento sem nenhuma certeza de que vai dar certo... Sem nenhuma chance ou seja, com uma baixa probabilidade de dar certo, quer?
E como que podemos medir o quão confiável é algo?
Imagina que estamos em uma indústria, com várias maquinas. Essas máquinas trabalham em conjunto muitas vezes, cada uma é responsável por uma função, mas elas funcionam independentes das outras, ou seja, se uma falhar não quer dizer que a outra irá falhar, tampouco irá atrapalhar a produção de uma outra.
Se for uma indústria têxtil, podemos falar que temos um tipo de máquina A que é responsável por cortar o tecido e a máquina B por costurar. Temos duas máquinas de cada tipo.
Teoria da Confiabilidade
Eu quero saber o quão confiável é essa minha indústria, ou seja, qual a probabilidade de dar tudo certo (ou seja, produzirmos roupas)?
Podemos nesse caso observar dois sistemas:
- Sistema 1: Máquina A e Máquina B
- Sistema 2: Os dois conjuntos de máquina AB
Para o sistema 1 funcionar precisamos que tanto a máquina A funcione, quanto a máquina B. É o tipo de sistema em série.
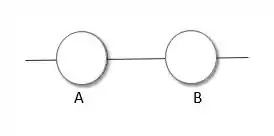
Digamos a probabilidade da máquina A funcionar e a probabilidade da máquina B funcionar. A probabilidade do sistema funcionar então será:
Onde: é a confiabilidade do componente i e a confiabilidade do sistema.
Para o sistema 2 funcionar precisamos que PELO MENOS um conjunto AB funcione. É o tipo de sistema em paralelo.
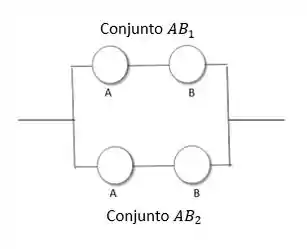
A probabilidade do sistema funcionar será:
Onde é a confiabilidade do componente 1 e 2 respectivamente.
Tudo bem até aqui? Vamos olhar os exercícios então!
Teoria da Confiabilidade
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,115-20
Na figura ao lado temos um sistema com três componentes funcionando independemente, com confiabilidades Obtenha a confiabilidade do sistema.
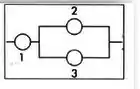
Passo 1
Vamos olhar para a figura e interpretar:
Os componentes 2 e 3 estão em paralelo e o componente 1 está em série com o “box” 23. Certo?
Já deu pra notar então que vamos ter que dividir esse problema em dois:
1º Encontrar a confiabilidade do sistema 23 (paralelo).
2º Encontrar a confiabilidade do sistema 1 e “box”
Note que esse para esse “box” utilizaremos a confiabilidade que calcularmos de 2 e 3.
Vamos então?
Passo 2
Confiabilidade Sistema 2-3:
Como está em paralelo, sabemos que:
Passo 3
Confiabilidade Sistema 1 – “box”
Como está em série, sabemos que:
Resposta
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,115-22
Supondo que todos os componentes do sistema da figura ao lado tenham a mesma confiabilidade e funcionem idependentemente, obtenha a confiabilidade do sistema.
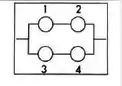
Passo 1
A primeira coisa a fazer é olhar o desenho e interpretar.
Pelo desenho percebemos que:
- Componentes 1 e 2 estão em série
- Componentes 3 e 4 estão em série
- Conjunto 12 está em paralelo com conjunto 34
A partir daí, vamos calcular!
Passo 2
- Confiabilidade dos Componentes 1 e 2 em série:
Passo 3
- Confiabilidade dos Componentes 3 e 4 em série:
Passo 4
-Confiabilidade do sistema composto pelo Conjunto 12 em paralelo com o Conjunto 34.
Resposta
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 125-48
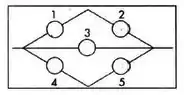
Na figura abaixo temos um sistema chamado ponte. Supondo que todos os componentes do sistema da figura tenham a mesma confiabilidade e funcionem independemente, obtenha a confiabilidade do sistema.
Passo 1
Qual a primeira coisa que devemos fazer SEMPRE em problemas de confiabilidade? Analisar a figura! Veja só:
- Componentes 1 e 2 estão em série
- Componentes 4 e 5 estão em série
- Conjunto 12 está em paralelo com 3, que está em paralelo com o Conjunto 45.
Vamos lá então?
Passo 2
- Confiabilidade dos componentes 1 e 2 (em série)
- Confiabilidade dos componentes 4 e 5 (em série)
Passo 3
- Confiabilidade Conjunto 12 com Componente 3 (paralelo)
- Confiabilidade do Conjunto 123 com o Conjunto 45
Resposta
Exercício Resolvido #4
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,126-57
Um sistema é composto de três componentes 1, 2 e 3, com confiabilidade 0,9; 0,8 e 0,7, respectivamente. O componente 1 é indispensável ao funcionamento do sistema; se 2 ou 3 não funcionam, o sistema funciona, mas com um rendimento inferior. A falha simultânea de 2 e 3 implica o não-funcionamento do sistema. Supondo que os componentes funcionem independentemente , calcular a confiabilidade do sistema.
Passo 1
Opa! Esse não tem desenho para interpretar... Mas tem o enunciado ué! Vamos reler com calma para entender o que ele falou:
O componente 1 é indispensável, ou seja, ele precisa estar em série. Por que eu afirmo isso? Ué, relembra a teoria comigo:
- Em série: Precisam ambos funcionarem. Se um não funcionar o sistema não funciona.
- Em paralelo: Precisa de pelo menos um funcionando para o sistema funcionar.
Então o componente 1 precisa estar em série, pois ser indispensável significa que sem ele o sistema não consegue funcionar.
E os componentes 2 e 3? Bom, no enunciado diz que se um deles não funcionar não tem problema.. o sistema continua funcionando (com um rendimento inferior). Ou seja, eles estão em paralelo.
Depois o enunciado fala: A falha simultânea de 2 e 3 implica no não funcionamento do sistema Isso reafirma o fato de que 2 e 3, o conjunto, precisa estar em série com 1.
Vamos ver como fica o desenho:
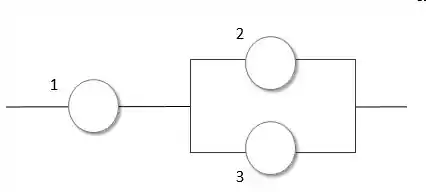
Passo 2
Então vamos calcular agora!
- Componentes 2 e 3 (em paralelo)
Passo 3
- Componente 1 e Conjunto 23 (em série)
Resposta
0.846
Exercício Resolvido #5
Elaboração Própria
Suponha um sistema composto por 4 elementos. O elemento 1 e o elemento 4 são indispensáveis para o fucionamento do sistema. O elemento 2 pode falhar sem impedir o funcionamento do sistema, idem para o elemento 3. Mas os elementos 2 e 3 não podem parar de funcionar ao mesmo tempo. Qual a confiabilidade do sistema? Assuma todas as confiabilidades como .
Passo 1
Vamos pensar no que foi falado. Elemento 1 e 4 são indispensáveis para o funcionamento, ou seja, são as estruturas sem paralelos. Já os elementos 2 e 3 podem falhar separadamente mas nunca ao mesmo tempo, então são elementos em paralelo. Desenhando temos algo assim:
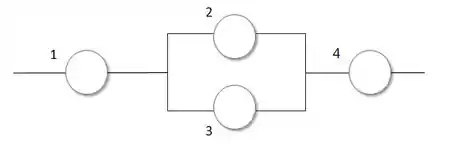
Passo 2
Vamos calcular primeiro a confiabilidade do Box em paralelo, ou seja, elementos 2 e 3:
Passo 3
Agora podemos colocar o elemento 1, o resultante do Box e o elemento 4 em série e teremos: