Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Estimador De Máxima Verossimilhança

Ver Todos os Exercícios

Teoria

Cara, vamos supor que você tem uma amostra de n notebooks e que a vida útil da bateria deles é sua variável X , sendo que:

X ~ E x p λ

Ou seja, X segue uma distribuição exponencial de parâmetro λ . Mas você não conhece esse tal de λ e tem que estimar ele a partir da sua amostra!

Bom, até agora tudo que a gente precisou estimar, tinha um estimador conhecido né? Mas, como nem tudo são flores, em muitos casos a escolha do estimador mais adequado não é tão fácil assim.

Existem alguns métodos que permitem construir estimadores. O mais importante deles é o método da máxima verossimilhança que é o título aqui do nosso tópico xD

Pra isso, vamos seguir um passo-a-passo:

Passo 1: Escrever a função de probabilidade.

No nosso caso, temos uma distribuição exponencial, então

f x , λ = λ ⋅ e - λ x

Passo 2: Chamar nosso parâmetro desconhecido de θ :

f x , θ = θ ⋅ e - θ x

Passo 3: Calcular nossa querida função de verossimilhança L θ :

L θ = f x 1 , θ ⋅ f x 2 , θ ⋅ … ⋅ f x n , θ = ∏ i = 1 n f ( x i , θ )

No nosso exemplo:

L θ = ∏ i = 1 n θ ⋅ e - θ x i = θ ⋅ e - θ x 1 × θ ⋅ e - θ x 2 × … × θ ⋅ e - θ x n

Multiplicando os θ em evidência e somando os expoentes do e :

L θ = θ n ⋅ e - θ x 1 + x 2 + … + x n = θ n ⋅ e - θ ∑ x i

Passo 4: Maximizar a função L θ

Bom, nesse passo vamos usar um macetinho. Bom, L θ e ln ⁡ L θ tem seu máximo no mesmo ponto! Então maximizar uma dá no mesmo que maximizar a outra, e normalmente maximizar o l n vai ser mais fácil pra gente porque normalmente vão aparecer exponenciais e o l n tem umas propriedades muito úteis!

Pra maximizar, basta derivar e igualar a zero, lembra? Então queremos: d ( ln ⁡ L ( θ ) d θ = 0

Do nosso exemplo:

ln ⁡ θ n ⋅ e - θ ∑ x i = ln ⁡ θ n + ln ⁡ e - θ ∑ x i = n ln ⁡ θ - θ ∑ x i

Derivando:

d n ln ⁡ θ - θ ∑ x i d θ = n θ - ∑ x i

Igualando a zero:

n θ - ∑ x i = 0

θ = n ∑ x i

Opa, lembra que nossa média amostral era justamente ∑ x i n ?! Então, encontramos nosso estimador de máxima verossimilhança!

θ = 1 x ¯

Agora partiu exercitar isso!

Exercícios Resolvidos

Exercício Resolvido #1

PUC – 2011.1 – P3 - Estimador de Máxima Verossimilhança

Seja X ~ E x p ( λ ) ; λ > 0 e X > 0 . Calcule:

  1. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.
  2. Admitindo-se que a X = ( 2,3 ; 3,0 ; 2,6 ; 2,2 ; 2,4 ) , qual seria o valor de "   λ   ̂ " .

Passo 1

(a)

Bom a gente tem uma variável que segue a distribuição exponencial, com parâmetro λ que precisamos estimar.

X ~ E x p ( λ )

A gente conhece a função de probabilidade da exponencial, lembra?

f x ; λ = λ . e - λ x

Passo 2

Primeira coisa, vamos chamar de θ o estimador de máximo verossimilhança para o parâmetro e calcular a sua função de verossimilhança.

L θ = ∏ i = 1 n θ . e - θ x

Quando a gente multiplica n vezes o θ , é a mesma coisa que elevar ele a n - é s i m a potência.

E quando multiplicamos n exponenciais é a mesma coisa que somar todos os expoentes da exponencial. Concorda? Quando multiplicamos exponenciais, somamos os expoentes.

Ficaria assim então:

L θ = θ n . e ∑ - θ x

Passo 3

Agora calculamos o l n .

ln ⁡ L θ = ln ⁡ θ n . e ∑ - θ x

= ln ⁡ θ n + ln ⁡ e ∑ - θ x

= n . ln ⁡ θ - ∑ i = 1 n θ x i

Passo 4

Pra finalizar calculamos a derivada e igualamos a zero.

d ln ⁡ L θ d θ = d n . ln ⁡ θ - ∑ i = 1 n θ x i d θ

= n θ - ∑ i = 1 n x i

Igualando isso a zero, teremos:

n θ - ∑ i = 1 n x i = 0

∑ i = 1 n x i = n θ

θ = n ∑ i = 1 n x i

Isso é a mesma coisa que dizer que nosso estimador de máxima verossimilhança é igual a:

θ = 1 x ¯

Passo 5

(b)

Pra gente descobrir o que queremos, primeiro temos que calcular a média desses valores e substituir na fórmula que a gente acabou de achar para o estimador.

x ¯ = 2,3 + 3 + 2,6 + 2,2 + 2,4 5 = 12,5 5 = 2,5

Com isso:

θ = 1 2,5 = 0,4

Resposta

a   θ = 1 x ¯

b   θ = 0,4

Exercício Resolvido #2

PUC – 2013.1 – P3 - Estimador de Máxima Verossimilhança

Este modelo probabilístico (paramétrico) é uma variável aleatória discreta, que modela um experimento em “ n ” repetições de uma Bernoulli até atingir o 1º sucesso.

Pergunta-se:

Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Passo 1

Primeira pergunta: que modelo probabilístico é esse? Lembra?

É o modelo geométrico, que tem a seguinte função de probabilidade:

P X = x = p 1 - p x - 1

Beleza?

É a partir disso que vamos estimar o parâmetro p desse modelo. Primeiro, substituímos ele por uma estimativa θ .

P X = x = θ . 1 - θ x - 1

Passo 2

Agora calculamos L ( θ ) .

L θ = ∏ i = 1 n θ . 1 - θ x - 1

Multiplicando n vezes um mesmo θ , temos θ n . A mesma ideia pode ser aplicada a outra parte da função, ficaríamos com:

L θ = θ n . 1 - θ ∑ i = 1 n x i - n

Passo 3

Calculamos ln ⁡ L θ .

ln ⁡ L θ = ln ⁡ ( θ n . 1 - θ ∑ i = 1 n x i - n )

= ln ⁡ θ n + ln ⁡ 1 - θ ∑ i = 1 n x i - n

= n . ln ⁡ θ + ∑ i = 1 n x i - n × ln ⁡ 1 - θ

Passo 4

Calcular a derivada desse l n em função do parâmetro estimado θ .

d ln ⁡ L θ d θ = n θ + n - ∑ i = 1 n x i 1 - θ

E igualamos essa derivada a zero para calcular o estimador de máxima verossimilhança.

- n θ = n - ∑ x i 1 - θ

- n + n θ = n θ - θ ∑ x i

n - θ ∑ x i = 0

θ = n ∑ x i    

Ou seja...

θ = 1 X ¯

Podemos substituir θ por θ M V , já que esse é o estimador de máxima verossimilhança.

θ M V = 1 X ¯

Resposta

θ M V = 1 X ¯

Exercício Resolvido #3

PUC – 2012.2 – P3 -

Queremos modelar tempos de duração de equipamentos, esta propriedade indica que a vida restante de um equipamento não depende da idade atual deste equipamento. Pergunta-se:

  1. Qual o modelo probabilístico que você adotaria para este experimento?
  2. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Passo 1

(a)

Pra modelar o tempo de duração de um equipamento precisamos de uma variável contínua, concorda? Isso era a primeira coisa que você tinha que notar, já que o tempo é algo contínuo né...

Qual das distribuições contínuas que a gente conhece melhor se enquadra pra representar o tempo... a exponencial.

X   ~   E x p o n e n c i a l   θ

θ é o parâmetro que a gente não conhece, que a gente vai estimar agora na letra (b).

Passo 2

(b)

Bom a gente tem uma variável que segue a distribuição exponencial, com parâmetro λ que precisamos estimar.

X ~ E x p ( λ )

A gente conhece a função de probabilidade da exponencial, lembra?

f x ; λ = λ . e - λ x

Passo 3

Primeira coisa, vamos chamar de θ o estimador de máximo verossimilhança para o parâmetro e calcular a sua função de verossimilhança.

L θ = ∏ i = 1 n θ . e - θ x

Quando a gente multiplica n vezes o θ , é a mesma coisa que elevar ele a n - é s i m a potência.

E quando multiplicamos n exponenciais é a mesma coisa que somar todos os expoentes da exponencial. Concorda? Quando multiplicamos exponenciais, somamos os expoentes.

Ficaria assim então:

L θ = θ n . e ∑ - θ x

Passo 4

Agora calculamos o l n .

ln ⁡ L θ = ln ⁡ θ n . e ∑ - θ x

= ln ⁡ θ n + ln ⁡ e ∑ - θ x

= n . ln ⁡ θ - ∑ i = 1 n θ x i

Passo 5

Pra finalizar calculamos a derivada e igualamos a zero.

d ln ⁡ L θ d θ = d n . ln ⁡ θ - ∑ i = 1 n θ x i d θ

= n θ - ∑ i = 1 n x i

Igualando isso a zero, teremos:

n θ - ∑ i = 1 n x i = 0

∑ i = 1 n x i = n θ

θ = n ∑ i = 1 n x i

Isso é a mesma coisa que dizer que nosso estimador de máxima verossimilhança é igual a:

θ = 1 x ¯

Já que x ¯ = ∑ x i n .

Resposta

a   X   ~   E x p   θ

b   θ ^ M V = 1 x ¯

Exercício Resolvido #4

PUC – 2013.2 – P3 -Estimador de Máxima Verossimilhança

Você é contratado para realizar pesquisas de opinião para um determinado candidato que está concorrendo a eleição presidencial de um dado sindicado. Cada pesquisa deve ser feita em uma amostra de n sindicalizados e estão previstas N repetições desta pesquisa. Determinar qual o modelo probabilístico que você adotaria para estimar a proporção de eleitores favoráveis a este candidato e deduza o estimador de máxima verossimilhança para tal parâmetro (proporção), mostrar todos os passos da solução.

Passo 1

Eu não conheço a probabilidade de cada sindicalizado escolher o candidato, vou chamar de p .

Vou ter que entrevistar n sindicalizados, cada um com a mesma probabilidade p de escolher o candidato... isso tem cara de que? Binomial, concorda? Os parâmetros que a gente tem na binomial são exatamente, n e p .

X   ~   B i n o m i a l   n , p

No caso, n   a gente “conhece”, o parâmetro desconhecido que a gente precisa estimar é o p .

Vou chamar ele de θ então...

X   ~   B i n   n ,   θ

Passo 2

Agora sim, vamos fazer o estimador de máxima verossimilhança pra esse parâmetro desconhecido.

Primeiro precisamos da função de probabilidade da Binomial.

f x = n x . θ x . 1 - θ n - x

Beleza?

Daí a gente obtém a função de verossimilhança...

L θ = ∏ i = 1 N n x . θ x . 1 - θ n - x

Esse operador aí é o que representa o produto dos termos...

A gente pode melhorar isso um pouco...

Se a gente multiplica N vezes o termo θ x , é a mesma coisa que repetir a base θ e somar todos os N expoentes x ...

θ ∑ i = 1 N x i

A mesma coisa pro 1 - θ n - x , a gente repete a base e soma todos os expoentes... fica assim...

1 - θ N n - ∑ i = 1 N x i

E o termo da combinatória não tem como simplificar não, deixa assim mesmo, aí fica...

L θ = ∏ i = 1 N n x . θ ∑ i = 1 N x i . 1 - θ N n - ∑ i = 1 N x i

Bem feio né? Vai melhorar.

Passo 3

Próximo passo é calcular ln ⁡ L θ .

= ln ⁡ ∏ i = 1 N n x . θ ∑ i = 1 N x i . 1 - θ N n - ∑ i = 1 N x i

l n de um produto, você pode separar na soma dos l n ...

= l n ∏ i = 1 N n x + ln ⁡ θ ∑ i = 1 N x i + ln ⁡ 1 - θ N n - ∑ i = 1 N x i

O termo da frente deixa quieto assim mesmo, que já já a gente vai dar um jeito nele... nos outros a gente pode dar aquele peteleco nos expoentes...

= l n ∏ i = 1 N n x + ∑ i = 1 N x i . ln ⁡ θ + N n - ∑ i = 1 N x i . ln ⁡ 1 - θ

Passo 4

Tá tenso o bagulho né? Calma.

Continuando, a gente calcula a derivada desse monstro aí...

Lembra que eu falei que ia dar um jeito nesse primeiro termo aí? Pois é, na derivada ele zera né? Pronto, não precisamos mais carregar ele.

De resto, fica:

d ln ⁡ L θ d θ = ∑ i = 1 N x i θ - N n 1 - θ + ∑ i = 1 N x i 1 - θ

Passo 5

Pra fechar, a gente iguala isso a zero, maximizando a função.

∑ i = 1 N x i θ - N n 1 - θ + ∑ i = 1 N x i 1 - θ = 0

Tirando mmc embaixo...

1 - θ . ∑ i = 1 N x i - N n . θ + θ . ∑ i = 1 N x i θ 1 - θ = 0

O denominador vai embora e fica...

1 - θ . ∑ i = 1 N x i - N n . θ + θ . ∑ i = 1 N x i = 0

∑ i = 1 N x i - θ . ∑ i = 1 N x i - N n . θ + θ . ∑ i = 1 N x i = 0

Viu que tem dois termos iguais aí com sinal contrário? Eles vão sumir agora, dá uma olhada...

∑ i = 1 N x i - N n . θ = 0

AGORA SIM! Chegou o momento tão esperado, só falta isolar o estimador θ ...

θ = ∑ i = 1 N x i N n

Passo 6

A gente pode tentar simplificar isso aí...

Ta ligado que...

x ¯ = ∑ i = 1 N x i N

Certo?

Então o θ fica...

θ = x ¯ n

Sempre fica ligado nessa parada da média amostral, x ¯ , geralmente dá pra simplificar usando ela, e aí você não perde ponto bobo na prova.

Pra não perder ponto nenhum mesmo e mitar, só substituir no final..

θ = θ ^ M V

θ ^ M V = x ¯ n

Resposta

θ ^ M V = x ¯ n

Exercício Resolvido #5

Elaboração Própria

Seja X 1 , X 2 , X 3 … uma amostra aleatória extraída de uma população com função densidade da forma:

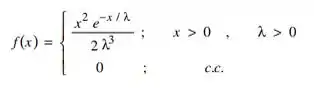
Identifique o estimador de máxima verosimilhança do parâmetro desconhecido, com base na amostra aleatória.

Passo 1

Nossa função de densidade já veio, e o parâmetro desconhecido dela é o λ . Vamos reescrevê-la com θ :

f x , θ = x 2 e - x θ 2 θ ³

Passo 2

Agora calculamos a função L ( θ ) , dada por:

L θ = ∏ i = 1 n x i 2 e - x i θ 2 θ ³

Lembrando que os índices i vão no x . Abrindo issaê:

L θ = x 1 2 e - x 1 θ 2 θ ³ × x 2 2 e - x 2 θ 2 θ ³ × x 3 2 e - x 3 θ 2 θ ³ … x n 2 e - x n θ 2 θ ³ = 1 2 θ 3 n × ∏ i = 1 n x i 2 × e - ∑ i = 1 n x i θ

Por enquanto mantemos esse produtório aí mesmo, já que não dá pra reescrevê-lo de nenhuma outra forma.

Passo 3

Agora aplicamos logaritmo natural na função que calculamos no passo anterior:

ln ⁡ L θ = ln ⁡ 1 2 θ 3 n × ∏ i = 1 n x i 2 × e - ∑ i = 1 n x i θ

Temos três produtos dentro desse logaritmo, vamos separá-los usando a propriedade dos produtos do logaritmo:

ln ⁡ L θ = ln ⁡ 1 2 θ 3 n + ln ⁡ ∏ i = 1 n x i 2 + ln ⁡ e - ∑ i = 1 n x i θ

Acabamos de falar da propriedade do produto, certo? Então vamos usá-la aqui de novo no produtório, que nada mais é que um produto n vezes. Se o logaritmo do produto é igual a soma dos logaritmos...

l n ∏ i = 1 n x i 2 = ∑ i = 1 n l n ⁡ ( x i ² )

Então reescrevendo nossa função log ⁡ L θ com essa substituição e usando a propriedade dos expoentes no logaritmo pra derrubar os expoentes:

ln ⁡ L θ = n ln ⁡ 1 2 θ 3 + 2 ∑ i = 1 n l n ⁡ ( x i ) + - ∑ i = 1 n x i θ ln ⁡ e

Como ln ⁡ e = 1 :

ln ⁡ L θ = n ln ⁡ 1 2 θ 3 + 2 ∑ i = 1 n l n ⁡ ( x i ) - ∑ i = 1 n x i θ

Passo 4

Agora derivamos o que acabamos de achar, em relação ao parâmetro desconhecido θ :

d ln ⁡ L θ d θ = d n ln ⁡ 1 2 θ 3 + 2 ∑ i = 1 n ln ⁡ x i - ∑ i = 1 n x i θ d θ

A derivada da soma é igual a soma das derivadas, então...

= d n ln ⁡ 1 2 θ 3 d θ + d 2 ∑ i = 1 n ln ⁡ x i d θ - d ∑ i = 1 n x i θ d θ

Podemos reparar que o segundo termo não tem θ , então a derivada dele vai ser zero.

Derivando o primeiro termo separadamente:

d n ln ⁡ 1 2 θ 3 d θ = n 2 θ 3 - 3 2 θ - 4 = - 3 n θ - 1 = - 3 n θ

Queee? Tendi nada! Aqui nós fizemos a regra da cadeia das derivadas! Primeiro derivamos o ln ⁡ 1 2 θ 3 como se fosse a derivada de ln ⁡ x , ou seja:

ln ⁡ 1 2 θ 3 → 2 θ 3

E depois multiplicamos o resultado pela derivada do 1 2 θ 3 , que vale:

1 2 θ 3 → - 3 2 θ - 4

Agora derivando o terceiro termo separadamente:

- d ∑ i = 1 n x i θ d θ = ∑ i = 1 n x i θ ²

Então, juntando todos os termos, nossa derivada fica:

d ln ⁡ L θ d θ = - 3 n θ + ∑ i = 1 n x i θ ²

Passo 5

Agora igualamos essa derivada a zero para achar o estimador:

d ln ⁡ L θ d θ = - 3 n θ + ∑ i = 1 n x i θ ² = 0

Multiplicando tudo por θ ² :

- 3 n θ + ∑ i = 1 n x i = 0

Isolando o θ :

θ = ∑ i = 1 n x i 3 n

Mas sabemos que ∑ i = 1 n x i n = X - , certo? É a fórmula da nossa média amostral, então:

θ M V = X - 3

Resposta

θ M V = X - 3

Exercícios de Livros Relacionados

Na função de verossimilhança L(p) da binomial, suponha que n = 5 e x = 3. Construa o gráfico da função para os possíveis valores de p = 1/5, 2/5, 3/5, 4/5, e verifique que o máximo ocorre realmente pa
Considere Y uma v.a. com distribuição de Poisson, com parâmetro λ0. Obtenha a EMV de λ, baseado numa amostra de tamanho n.
Observa-se uma seqüência de ensaios de Bernoulli, independentes, com parâmetro p, até a ocorrência do primeiro sucesso. Se X indicar o número de ensaios necessários, usando uma moeda, repetiu-se esse
Suponha que X seja uma v.a. com distribuição normal, com média μ e variância 1.Obtenha o EMV de μ, para uma amostra de tamanho n, (x1, ..., xn).
Considere o modelo de efeitos aleatórios para o planejamento completamente aleatorizado com um único fator. Mostre que um intervalo de confiança de 100 1 - α % para a razão dos componentes de variânci