Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Estimador Não Tendencioso e EQM

Ver Todos os Exercícios

Teoria

Estimador não tendencioso

Já jogou Tiro ao alvo? Vai ser útil pela primeira vez na sua vida haha..

Vamos supor três atiradores: A,B e C.

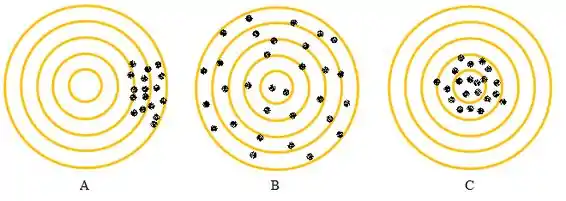
Vamos fazer uma primeira análise dessa parada:

  • Atirador A → É preciso, mas tá tendencioso pra direita, longe do centro.
  • Atirador B → É bizonho, mas até que acerta de vez em quando.
  • Atirador C → Esse é sinistro, precisão é o sobrenome.

Uma ideia básica pra um bom estimador seria o que? Que o valor que a gente espera dele seja o mais próximo possível do valor real do parâmetro que a gente tá estimando, concorda?

Dessa ideia, vem o conceito de estimador não tendencioso.

A gente vai dizer que um estimador qualquer θ ~ é não tendencioso se a esperança (valor médio) dele for igual ao valor do parâmetro θ que estamos estimando.

E θ ^ = θ

Olhando pros nossos atiradores a gente percebe que o A é tendencioso, concorda? O valor médio dele não coincide com o centro, ele tem meio que uma tendência pra direita do alvo.

Enquanto os outros não são tendeciosos, o B não possui tendência e o C a tendência dele é o próprio centro.

Tem um outro conceito que a gente pode colocar aqui, que é o viés, B θ ^ .

Viés de θ ~ é a diferença entre o seu valor esperado e o valor do parâmetro.

B θ ^ = E θ ^ - θ

Se o viés é igual a zero, o estimador é não tendencioso.

Erro quadrático médio

Bom, além de ser não tendencioso, é importante também que esse estimador gere estimativas que estejam próximas do verdadeiro valor do parâmetro!

Além de ser não tendecioso, o estimador tem que ser preciso.

De que adianta eu fazer estimativas que tenham uma média(esperança) próxima do valor certo, mas que tenha valores muito discrepantes? O atirador B , por exemplo! Adianta de nada ele acertar o centro de vez em quando se ele tem uma precisão horrível.

A gente mede essa precisão através do Erro Quadrático Médio ou E Q M !

E Q M θ ^ = V a r θ ^ + B θ ^ 2

Bom, claramente a gente percebe que o atirador B tem sérios problemas com precisão, enquanto os outros não.

Confere aí se você realmente entendeu esses conceitos com a tabela abaixo:

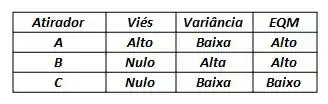
Erro quadrático médio

Exercícios Resolvidos

Exercício Resolvido #1

PF - 2014.2

Seja X uma v.a. com média µ e variância σ ² . Seja X 1 , … , X n uma amostra aleatória de X . A partir desta amostra aleatória, podemos construir o estimador X ^ ≔ 1 n - 1 ∑ i = 1 n X i para a média.

  1. Calcule o viés deste estimador.
  2. Calcule o erro quadrático médio deste estimador.
  3. Ao comparar X ^ e X ¯ , qual deles é mais indicado para estimar µ ? Justifique.

Passo 1

(a)

Lembra da fórmula do viés? Vamos aplicar para o caso de um estimador pra média.

B X ^ = E X ^ - μ

Temos que calcular essa esperança aí.

E X ^ = E 1 n - 1 ∑ i = 1 n X i

E vamos aplicar as propriedades de combinação linear da esperança.

= 1 n - 1 . ∑ i = 1 n E X i

A esperança de X , a gente conhece:

E X i = μ

Daí fica:

= n μ n - 1

Passo 2

E com isso, calculamos o viés.

B X ^ = E X ^ - μ

= n μ n - 1 - μ

= n μ - n μ + μ n - 1

= μ n - 1

Passo 3

(b)

Mais uma fórmula que você precisa lembrar ein, do erro quadrático médio...

E Q M X ^ = V a r X ^ + B X ^ 2

Precisamos calcular a variância antes...

V a r X ^ = V a r 1 n - 1 ∑ i = 1 n X i

Aplicando as propriedades da variância agora:

= 1 n - 1 2 . ∑ i = 1 n V a r X i

E:

V a r X i = σ ²

Fica então:

= n σ 2 n - 1 2

Passo 4

Daí a gente junta tudo de novo e calcula o erro quadrático...

E Q M X ^ = n σ 2 n - 1 ² + μ n - 1 2

= n σ 2 + μ 2 n - 1 2

Passo 5

(c)

Primeiro você precisaria saber o viés e o erro quadrático média da média X ¯ pra poder comparar, que são:

B X ¯ = 0

E Q M X ¯ = σ 2 n

Se você comparar com os de X ^ , vai ver que... como o viés de X ¯ é zero (o que indica que é um estimador não tendencioso) e o de X ^ não é zero (estimador tendencioso).

E comparando a partir do erro quadrático médio, você tem que:

E Q M X ^ > E Q M X ¯

E quanto maior o erro quadrático médio, pior é o estimador.

Ou seja, o X ¯ é o melhor estimador.

Resposta

a μ n - 1

b n σ 2 - μ n - 1 2

c   X ¯   é   o   m e l h o r   e s t i m a d o r

Exercício Resolvido #2

P2- 2014.2 – UFRJ Estimador e Erros

Sejam X 1 , X 2 , … , X n uma amostra aleatória da variável aleatória X com distribuição Bernoulli ( p ) .

  1. Qual a distribuição de Y = X 1 + X 2 + … + X n ?
  2. Considere os dois seguintes estimadores para p : T 1 = Y n e T 2 = Y + n 2 n + n . Esses estimadores são não tendenciosos (não viciados) para p ?
  3. Expresse o erro quadrático médio E Q M desses dois estimadores em função de n e p .
  4. Suponha n = 4 e faça um único gráfico mostrando o comportamento do E Q M em função de p para os dois estimadores.

Passo 1

(a)

Cada x i tem a mesma distribuição Bernoulli (com a mesma prob. de sucesso p ) e o Y vai ser a soma de vários x i .

Quando eu tenho um mesmo experimento Bernoulli sendo repetido várias vezes, o que que eu tenho na verdade? Uma Binomial, concorda? A gente viu isso.

Então podemos dizer que...

Y   ~   B i n n , p

Passo 2

(b)

Você lembra o que faz um estimador ser não tendencioso? É quando o valor esperado pra ele é igual ao valor do parâmetro que a gente tá estimando.

E θ ^ = θ

Certo?

Então o que eu tenho que fazer nesses dois casos é calcular a esperança desses estimadores T 1 e T 2 e ver se dá igual a p ou não.

Se der, é não tendencioso, se não der, só lamento :D

Passo 3

Vamos fazer isso pro primeiro caso então...

E T 1 = E Y n

Pela propriedade da esperança, posso jogar pra fora o 1 n ...

E T 1 = E Y n

A gente acabou de ver que Y tem distribuição Binomial com parâmetros n e p .

Qual a esperança de uma variável que segue a Binomial?

E Y = n p

Certo?

Aí você junta tudo...

E T 1 = n p n

E T 1 = p

Opa! A esperança do estimador deu igual ao valor do parâmetro...

Isso significa que T 1 é um estimador não tendencioso de p .

Passo 4

Agora vamos ver esse segundo estimador aí, um pouco mais assustador...

E T 2 = E Y + n 2 n + n

Pera, não se assuste... concorda comigo que tudo isso aí que tem n são constantes? Variável mesmo só Y .

Então vamos usar algumas propriedades da esperança...

Tudo que multiplica a variável você pode tirar pra fora.... aí fica:

E T 2 = 1 n + n × E Y + n 2

Agora eu tenho a esperança de uma variável mais uma constante... também posso tirar essa constante pra fora...

E T 2 = 1 n + n × n 2 + E Y

Agora sucesso, só temos a E Y , que a gente já conhece lá do primeiro estimador que a gente fez, concorda?

E Y = n p

Jogando ali em cima...

E T 2 = n p + n 2 n + n

Mesmo que você mexa nesse capeta aí, você acha que isso é igual a p ? Não né! Então:

E T 2 = n p + n 2 n + n ≠ p

A gente conclui que T 2 é um estimador tendencioso do parâmetro p .

Passo 5

(c)

Agora a gente tem que calcular o E Q M dos dois estimadores, você lembra da fórmula?

E Q M θ ^ = V a r θ ^ + B θ ^ 2

Então antes a gente precisa calcular esses dois camaradas que apareceram aí.

Esse B θ ^ é o víeis... lembra dele?

B θ ^ = E θ ^ - θ

É a esperança do estimador (que a gente calculou no item anterior) menos o real valor do parâmetro.

Passo 6

Vamos calcular primeiro os viés (vieses... sla, não sou muito bom nisso) dos dois estimadores..

Pra T 1 ...

B T 1 = E T 1 - p

A gente calculou antes que:

E T 1 = p

Então:

B T 1 = p - p = 0

A gente já esperava isso né, como T 1 é não tendencioso, seu viés é zero.

Passo 7

Pra T 2 ...

B T 2 = E T 2 - p

A gente achou que:

E T 2 = n p + n 2 n + n

Então:

B T 2 = n p + n 2 n + n - p

Aí vamos abrir isso aí...

= n p + n 2 - n p - n p n + n

Opa, a gente corta um candango ali..

= n 2 - n p n + n

Vamos colocar n   em evidência...

= n 1 2 - p n n + 1

Aí a gente corta ele...

B T 2 = 1 2 - p n + 1

Show, vamos seguir e calcular a variância dos dois estimadores...

Passo 8

Pra T 1 ...

V a r T 1 = V a r Y n

Agora se liga que a gente vai usar as propriedades da variância, que são um pouquinho diferentes das da esperança... agora, a constante que multiplica a gente coloca pra fora elevando ao quadrado, e as constantes que a gente estiverem somando viram zero.

= 1 n 2 × V a r Y

Hmmm.. variância de Y ... vamos pensar igual a gente pensou pra esperança.

Y tem uma distribuição Binomial, qual a variância de uma distribuição dessa?

V a r Y = n p 1 - p

Juntando tudo...

V a r T 1 = n p 1 - p n 2

Simplificando:

V a r T 1 = p 1 - p n

Passo 9

Pra T 2 ...

V a r T 2 = V a r Y + n 2 n + n

Tá, vamos usar as propriedades...

  • O denominador que tá multiplicando, vem pra fora elevado ao quadrado;
  • O candango que tá somando Y ali, vai sumir.

= V a r Y n + n 2

V a r Y a gente já conhece.. fica então:

V a r T 2 = n p 1 - p n + n 2

Vou tentar melhorar isso aí pra a gente...

= n p 1 - p n n + 1 2

Coloquei n em evidência embaixo... aí agora vou elevar ela ao quadrado...

= n p 1 - p n n + 1 2

Aí some o n em cima e embaixo...

V a r T 2 = p 1 - p n + 1 2

Fiz isso porque a gente vai somar com o viés né, aí coloquei com denominadores parecidos pra facilitar nossa vida.

Passo 10

E agora? Agora tu já nem sabe o que tá fazendo né? Kkkk calma..

Finalmente a gente pode calcular o E Q M dos dois estimadores..

E Q M T 1 = B T 1 2 + V a r T 1

B T 1 = 0

E Q M T 1 = V a r T 1

V a r T 1 = p 1 - p n

Então:

E Q M T 1 = p 1 - p n

Passo 11

Agora pra T 2 :

E Q M T 2 = B T 2 2 + V a r T 2

B T 2 = 1 2 - p n + 1

V a r T 2 = p 1 - p n + 1 2

Então:

E Q M T 2 = 1 2 - p n + 1 2 + p 1 - p n + 1 2

= 1 2 - p 2 + p 1 - p n + 1 2

Abrindo os parênteses de cima...

= 1 4 - p + p 2 + p - p 2 n + 1 2

Corta um monte de candango aí...

E Q M T 2 = 1 4 n + 1 2

Falta pouco pra acabar..

Passo 12

(d)

Vamos pegar de novo os dois E Q M ' s :

E Q M T 1 = p 1 - p n

E Q M T 2 = 1 4 n + 1 2

Agora vamos fazer n = 4 ...

E Q M T 1 = p 1 - p 4

E Q M T 2 = 1 4 4 + 1 2

E Q M T 2 = 1 36

A gente tem que fazer o gráfico dessas duas funções agora...

Passo 13

Pra T 2 bem simples né.. T 2 é constante e igual a 1 36 . Então vamos ter uma reta na horizontal...

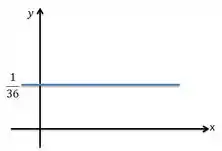
Passo 14

Para T 1 a gente vai ter uma parábola...

p 1 - p 4 = 0

p 1 - p = 0

p = 0     o u     p = 1

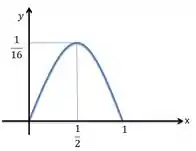
Agora sim, fim de papo.

Deu um certo trabalho, mas concorda comigo que, sabendo as fórmulas e as propriedades, a dificuldade maior eram as contas! Não se assuste com esse tipo de questão mais, beleza?

Resposta

a   Y   ~   B i n   n , p

b   B T 1 = 0     e     B T 2 = 1 2 - p n + 1

c   E Q M T 1 = p 1 - p n     e     E Q M T 2 = 1 4 n + 1 2

d   i m a g e n s

Exercício Resolvido #3

Elaboração própria

Considere uma amostra aleatória ( X 1 , X 2 , … , X n ) de uma v.a. X com distribuição normal. Mostre se a variância amostral s ² é um estimador tendencioso ou não para a variância populacional σ ² .

Lembrar que:

s 2 = ∑ x i 2 - n . x ¯ 2 n - 1

Passo 1

Primeira coisa... lembrar o critério pra um estimador ser tendencioso ou não.

A esperança de um estimador não tendencioso é igual ao valor do parâmetro estimados.

O valor do parâmetro que no caso é a variância populacional é σ ² .

A gente vai então ter que calcular a esperança do s ² e ver se dá igual a σ ² . Pegou a ideia?

Passo 2

Vamos calcular então E [ s 2 ] .

E s 2 = E ∑ x i 2 - n . x ¯ 2 n - 1

= 1 n - 1 E ∑ x i 2 - n . x ¯ 2

Até aqui beleza? Só tirei o que tava constante pra fora.

Passo 3

Vamos calcular essa parte agora separado...

E ∑ x i 2 - n . x ¯ 2 = E ∑ x i 2 - n . E x ¯ 2

Apliquei uma propriedade da esperança..

Vendo por partes.. vamos analisar primeiro o x ¯ ² .

A gente sabe que..

E ( x ¯ 2 ) = V a r x ¯ + E x ¯ ²

Essa é uma relação entre a esperança e a variância de uma variável.

E esses valores a gente já conhece.. (dá uma olhada lá no conteúdo do capítulo)

V a r x ¯ = σ 2 n   ,     E x ¯ = μ

Então..

E x ¯ 2 = σ 2 n + μ ²

Passo 4

Vamos analisar agora E ∑ x i 2 .

Se fosse só E x i 2 , a gente faria assim..

E x i 2 = V a r x i + E [ x i ] ²

A gente sabe que V a r x i = σ ² e que E x i = μ .

Ai ficaria..

E x i 2 = σ ² + μ ²

Como temos o somatório de n valores de X , basta multiplicarmos isso que encontramos por n .

E ∑ x i 2 = n σ ² + n μ ²

Passo 5

Vamos juntar agora e tirar nossa conclusão.

E s 2 = 1 n - 1 E ∑ x i 2 - n . x ¯ 2

E s 2 = E ∑ x i 2 - n . E x ¯ 2 n - 1

Substituindo pelos valores que a gente encontrou.

E s 2 = n σ 2 + n μ 2 - n . σ 2 n + μ 2 n - 1

Multiplicando o n pra dentro do colchete.

E s 2 = n σ 2 - σ 2 n - 1

Colocando em evidência o σ ² .

E s 2 = n - 1 . σ 2 n - 1

E s 2 = σ ²

Opa!! E agora? Esse é o momento em que você já não sabe mais o que está fazendo haha..

O que a gente acabou de descobrir é que a esperança do s ² é igual ao valor do parâmetro que a gente queria σ ² .

Isso quer dizer que s ² é um estimador não tendencioso para a variância populacional σ ² .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

P2- 2012.2 – UFRJ Estimador e Erros

Suponha que a variável aleatória

T : t e m p o   e n t r e   c h e g a d a s   c o n s e c u t i v a s   d e   c l i e n t e s   n a   f i l a   d e   u m   b a n c o

siga distribuição Exponencial com parâmetro l â m b d a desconhecido, e tome T 1 ,   … ,   T n uma amostra aleatória de T . Denote por φ a mediana de T (lembre que ∫ - ∞ φ f t d t =   1 2 , com f t a função de densidade da v.a. T ), e seja T m d = l n 2 T ¯ um estimador de φ , em que T denota a média amostral de ( T 1 ,   … ,   T n ) .

  1. T m d é um estimador não-tendencioso para φ ? Por quê?
  2. Obtenha o erro médio quadrático de T m d como estimador de φ .

Passo 1

(a)

Um estimador é não-tendencioso quando o valor esperado é igual o valor do parâmetro.

Primeiro a gente tinha que lembrar que:

f t → T

f ( t ) é a função que representa a variável T . E que é igual a:

f t = λ ⋅ e - λ t

Nesse exercício a gente tem uma estimação para a mediana representada por φ . Maaas, você precisaria lembrar que a mediana representa metade do valor total da função f ( t ) , ou seja:

∫ - ∞ φ f t d t =   1 2

Passo 2

Resolvendo a integral anterior.

∫ - ∞ φ λ ⋅   e - λ t d t =   1 2

1 - e - λ φ = 1 2

e - λ φ = 1 2

- λ φ = ln ⁡ 1 2

φ = - ln ⁡ 1 2 λ

φ = - ln ⁡ 1 - ln ⁡ 2 λ

φ = ln ⁡ 2 λ

Passo 3

O estimador que a gente tem é:

T m d = l n 2 T ¯

Vamos ver qual é o valor esperado pra ele:

E T m d = E l n 2 T ¯  

E T m d = l n 2 E T ¯

E T ¯ = E ∑ t i n = 1 n × E ∑ t i = 1 n × E n × T = 1 n × n × E T

E T m d = ln ⁡ 2 × E T

A variável T , nesse caso, tem esperança igual a 1 / λ . Lembra disso? Tá lá no início da teoria, na parte de probabilidade. Então:

E T m d = ln ⁡ 2 λ

A gente conclui, então, que o valor esperado realmente é igual ao valor do parâmetro mediana. Por isso, o estimador pode ser considerado não-tendencioso.

Passo 4

(b)

E Q M T m d = V a r T m d

V a r T m d = V a r ln ⁡ 2 T ¯

= ln ⁡ 2 2 × V a r T ¯

= ln ⁡ 2 2 × V a r ∑ t i n

= ln ⁡ 2 2 × 1 n 2 × V a r ∑ t i

= ln ⁡ 2 2 × 1 n 2 × n × V a r T

Lembrando novamente também que V a r T = 1 λ 2

= ln ⁡ 2 2 n λ 2

= φ 2 n

Resposta

a   É um estimador não-tendencioso

b   E Q M T m d = φ 2 n

Exercício Resolvido #5

Estimador e Erros

Um administrador do governo quer avaliar a proporção p de aprovação da comunidade sobre determinado projeto. Para isso fez uma pesquisa de opinião selecionando ao acaso 40 pessoas da população de interesse. Considerando 1 = favorável e 0 = desfavorável, temos então 40 variáveis aleatórias iid X 1 , X 2 , … , X 40 , todas elas com distribuição de Bernoulli p . Considere as quatro seguintes alternativas de estimador para p :

p ^ A = X 10 + X 20 + X 30 + X 40 4     ,     p ^ B = X 10 + 2 X 20 + 3 X 30 + 4 X 40 10     ,     p ^ C = ∑ i = 1 40 X i 40       ,     p ^ D = ∑ i = 1 10 X i + 2 . ∑ i = 11 20 X i + 3 . ∑ i = 21 30 X i + 4 . ∑ i = 31 40 X i 100

  1. Qual é o viés (ou vício) de cada um desses estimadores?
  2. Expresse o erro quadrático média E Q M de cada um deles em função de p . Ordene esses estimadores em termos de seus E Q M , e diga qual é o melhor de acordo com esse critério.
  3. Se os dados coletados foram:

10001       11111       10111       11110       11000       11111       11111       11100

Qual é a estimativa de p para cada uma das quatro alternativas?

Passo 1

(a)

Temos variáveis aleatórias iid, todas com distribuição Bernoulli p .

X i   ~   B e r n o u l l i p

Bom lembrar que:

E X i = p     e     V a r X i = p 1 - p

E temos quatro estimadores para p e vamos calcular o viés de cada um.

A fórmula do viés é:

B p ^ = E p ^ - p

Onde p ^ são os estimadores que a gente tem.

A gente precisa então calcular primeiro E p ^ de cada estimador.

Passo 2

Pra fazer isso a gente vai ter só que aplicar aquelas propriedades de esperança de uma combinação linear.

Vamos lá, um por um:

p ^ A = X 10 + X 20 + X 30 + X 40 4

E p ^ A = E X 10 + E X 20 + E X 30 + E X 40 4

A gente sabe que:

E X i = p

Daí:

E p ^ A = 4 p 4 = p

E aí o viés será:

B p ^ A = p - p

B p ^ A = 0

Passo 3

Para p ^ B :

p ^ B = X 10 + 2 X 20 + 3 X 30 + 4 X 40 10    

E p ^ B = E X 10 + 2 . E X 20 + 3 . E X 30 + 4 . E X 40 10

Daí:

E p ^ B = p + 2 p + 3 p + 4 p 10 = 10 p 10 = p

E o viés será:

B p ^ B = E p ^ B - p

= p - p

B p ^ B = 0

Passo 4

Para p ^ C :

p ^ C = ∑ i = 1 40 X i 40

E p ^ C = 40 . E X i 40 = 40 p 40 = p

E o viés:

B p ^ C = E p ^ C - p

= p - p

B p ^ C = 0

Passo 5

Pra fechar, p ^ D :

p ^ D = ∑ i = 1 10 X i + 2 . ∑ i = 11 20 X i + 3 . ∑ i = 21 30 X i + 4 . ∑ i = 31 40 X i 100

E p ^ D = 10 . E X i + 2 × 10 . E X i + 3 × 10 . E X i + 4 × 10 . E X i 100

E p ^ D = 100 p 100 = p

E o viés:

B p ^ D = E p ^ D - p

= p - p

B p ^ D = 0

Viu? Não tem muito mistério, era só lembrar que a esperança de uma variável Bernoulli é p e as propriedades da esperança.

Passo 6

(b)

Pra expressar o E Q M primeiro a gente tem que lembrar da fórmula:

E Q M p ^ = V a r p ^ + B p ^ 2

A gente já sabe que todos os viés são zero, falta calcular as suas variâncias, e vamos ter:

E Q M p ^ = V a r p ^

De novo, vamos fazer um por um...

Para p ^ A :

p ^ A = X 10 + X 20 + X 30 + X 40 4

V a r p ^ A = V a r X 10 + X 20 + X 30 + X 40 4

= 1 16 . V a r X 10 + V a r X 20 + V a r X 30 + V a r X 40

Lembrando que V a r X i = p 1 - p .

= 4 p 1 - p 16

V a r p ^ A = p 1 - p 4

E daí a gente tira o E Q M .

E Q M p ^ A = V a r p ^ A

E Q M p ^ A = p 1 - p 4

Passo 7

Para p ^ B .

p ^ B = X 10 + 2 X 20 + 3 X 30 + 4 X 40 10    

V a r p ^ B = 1 100 . V a r X 10 + 4 . V a r X 20 + 9 . V a r X 30 + 16 . V a r X 40

= 30 p 1 - p 100

E daí:

E Q M p ^ B = 30 p 1 - p 100

Passo 8

Para p ^ C :

p ^ C = ∑ i = 1 40 X i 40

V a r p ^ C = 1 40 2 . ∑ i = 1 40 V a r X i

= 40 . V a r X i 40 2

= p 1 - p 40

E:

E Q M p ^ C = p 1 - p 40

Passo 9

Fechando:

p ^ D = ∑ i = 1 10 X i + 2 . ∑ i = 11 20 X i + 3 . ∑ i = 21 30 X i + 4 . ∑ i = 31 40 X i 100

V a r p ^ D = 1 100 2 . 10 . V a r X i + 4 × 10 . V a r X i + 9 × 10 . V a r X i + 16 × 10 . V a r X i

= 300 p 1 - p 100 ²

E:

E Q M p ^ D = 3 p 1 - p 100

Passo 10

Vamos ordená-los agora:

E Q M p ^ A = p 1 - p 4 = 0,25 p 1 - p

E Q M p ^ B = 30 p 1 - p 100 = 0,30 p 1 - p

E Q M p ^ C = p 1 - p 40 = 0,025 p 1 - p

E Q M p ^ D = 0,03 p 1 - p

Colocando em ordem crescente, do menor para o maior E Q M ...

p ^ C < p ^ D < p ^ A < p ^ B

E o melhor estimador é aquele que tem o menor E Q M , logo é o p ^ C .

Passo 11

(c)

Os dados coletados são:

10001       11111       10111       11110       11000       11111       11111       11100

Vamos ter que calcular p ^ de cada estimador.

Tranquilo... só você identificar o x i (se é zero ou um) e colocar nas fórmulas.

p ^ A = X 10 + X 20 + X 30 + X 40 4

= 1 + 0 + 1 + 0 4

p ^ A = 0,5

p ^ B = X 10 + 2 X 20 + 3 X 30 + 4 X 40 10

= 1 + 2 × 0 + 3 × 1 + 4 × 0 10 = 4 10

p ^ B = 0,4

p ^ C = ∑ i = 1 40 X i 40

= 1 + 0 + 0 + 0 + 1 + … + 1 + 0 + 0 40 = 30 40

p ^ C = 0,75

p ^ D = ∑ i = 1 10 X i + 2 . ∑ i = 11 20 X i + 3 . ∑ i = 21 30 X i + 4 . ∑ i = 31 40 X i 100

= 7 + 2 × 8 + 3 × 7 + 4 × 8 100 = 76 100

p ^ D = 0,76

Resposta

a   T o d o s   o s   v i é s   s ã o   0

b   p ^ C < p ^ D < p ^ A < p ^ B   p ^ C   é   o   m e l h o r

c   p ^ A = 0,5   ; p ^ B = 0,4     ; p ^ C = 0,75     ; p ^ D = 0,76

Exercícios de Livros Relacionados

Uma v.a. X tem distribuição normal com média 10 e desvio padrão 4. Aos participantes de um jogo é permitido observar uma amostra de qualquer tamanho e calcular a média amostral. Ganha um prêmio aquele
Os dados abaixo referem-se ao índice de inflação (yt) de 1967 a 1979.Qual seria a inflação em 1981?
No Problema 7, determinamos os estimadores de mínimos quadrados para o modelo yt= f(t) + εt, no qual f(t) = α + βt. Suponha agora que.ou seja, temos n valores fixos x1, ..., xn de uma variável fixa (n
Como você usaria uma tabela (ou um gerador) de números aleatórios para sortear uma amostra nas seguintes situações:(b) 10 alunos de sua escola;
Como você usaria uma tabela (ou um gerador) de números aleatórios para sortear uma amostra nas seguintes situações:(a) 5 alunos de sua classe;