Exercícios de Estimador De Máxima Verossimilhança - Lista de Exercícios Resolvida

Este modelo probabilístico (paramétrico) é uma variável aleatória discreta, que modela um experimento em “” repetições de uma Bernoulli até atingir o 1º sucesso.

Pergunta-se:

Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Seja ; e . Calcule:

1. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.
2. Admitindo-se que a , qual seria o valor de .

Seja uma amostra aleatória extraída de uma população com função densidade da forma:

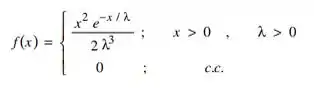
Identifique o estimador de máxima verosimilhança do parâmetro desconhecido, com base na amostra aleatória.

Você é contratado para realizar pesquisas de opinião para um determinado candidato que está concorrendo a eleição presidencial de um dado sindicado. Cada pesquisa deve ser feita em uma amostra de sindicalizados e estão previstas repetições desta pesquisa. Determinar qual o modelo probabilístico que você adotaria para estimar a proporção de eleitores favoráveis a este candidato e deduza o estimador de máxima verossimilhança para tal parâmetro (proporção), mostrar todos os passos da solução.

Queremos modelar tempos de duração de equipamentos, esta propriedade indica que a vida restante de um equipamento não depende da idade atual deste equipamento. Pergunta-se:

1. Qual o modelo probabilístico que você adotaria para este experimento?
2. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Tem-se um modelo probabilístico descrito por uma variável aleatória discreta que modela o seguinte experimento: repete-se o experimento de uma distribuição Bernoulli com probabilidade de sucesso até atingir o primeiro sucesso.

Determine qual é o modelo probabilístico que deve ser adotado para estimar o parâmetro desta função de probabilidade e deduza o estimador de máxima verossimilhança para tal parâmetro, detalhe todos os passos da solução.

Seja ; e . Calcule:

1. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.
2. Admitindo-se que a , qual seria o valor de .

Você é contratado para realizar pesquisas de opinião para um determinado candidato que está concorrendo a eleição presidencial de um dado sindicato. Cada pesquisa deve ser feita em uma amostra de sindicalizados e estão previstas repetições desta pesquisa. Determinar qual o modelo probabilístico que você adotaria para estimar a proporção de eleitos favoráveis a este candidato e deduza o estimador de máxima verossimilhança para o tal parâmetro (proporção).

Qual o estimador de máxima verossimilhança para o parâmetro de uma variável aleatória de Bernoulli escalada por uma constante conhecida? Ou seja, de um modelo cuja variável aleatória assuma o valor igual a (valor conhecido) com probabilidade e com probabilidade . Mostre todos os passos do desenvolvimento da solução.

Tem-se um modelo probabilístico (paramétrico) descrito por uma variável aleatória discreta, que modela o seguinte experimento: repete-se o experimento de Bernoulli com probabilidade de sucesso até se atingir o primeiro sucesso.

Pergunta-se: Que modelo é este e qual o estimador de máxima verossimilhança do parâmetro deste modelo probabilístico? (mostrar todos os passos da solução).

Você é contratado para realizar pesquisas de opinião para um determinado candidato que está concorrendo a eleição presidencial de um dado sindicado. Cada pesquisa deve ser feita em uma amostra de sindicalizados e estão previstas repetições desta pesquisa. Determinar qual o modelo probabilístico que você adotaria para estimar a proporção de eleitores favoráveis a este candidato e deduza o estimador de máxima verossimilhança para tal parâmetro (proporção), mostrar todos os passos da solução.

Suponha que a variável aleatória tenha a seguinte função de densidade de probabilidade:

Seja uma amostra aleatória de tamanho . Ache o estimador de máxima verossimilhança do parâmetro .

Tem-se um modelo probabilístico (paramétrico) descrito por uma variável aleatória discreta, que modela o seguinte experimento: repete-se o experimento de Bernoulli com probabilidade "" de sucesso até obter o -ésimo sucesso. Pede-se: Qual é o modelo probabilístico que deve ser adotado para estimar este parâmetro? Deduza o estimador de máxima verossimilhança para tal parâmetro

Tem-se um modelo probabilístico descrito por uma variável aleatória discreta que modela o seguinte experimento: repete-se o experimento de uma distribuição Bernoulli com probabilidade de sucesso até atingir o primeiro sucesso.

Determine qual é o modelo probabilístico que deve ser adotado para estimar o parâmetro desta função de probabilidade e deduza o estimador de máxima verossimilhança para tal parâmetro, detalhe todos os passos da solução.

Todo ano acontece no campus da PUC-Rio a Mostra PUC. Nesta Mostra são convidadas diversas empresas para apresentarem palestras. O reitor da PUC gostaria de saber quantos carros BMW entram diariamente no campus com pessoas que vão participar do evento. Você é contratado para realizar uma pesquisa de entrada deste veículo, sabendo-se que se trata de um evento raro. Determine e justifique qual o modelo probabilístico que você adotaria para estimar este parâmetro e deduza o estimador de máxima verossimilhança para tal parâmetro, detalhe todos os passos da solução.

Queremos modelar tempos de duração de equipamentos, esta propriedade indica que a vida restante de um equipamento não depende da idade atual deste equipamento. Pergunta-se:

1. Qual o modelo probabilístico que você adotaria para este experimento?
2. Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Este modelo probabilístico (paramétrico) é uma variável aleatória discreta, que modela um experimento em “” repetições de uma Bernoulli até atingir o 1º sucesso.

Pergunta-se:

Qual o estimador de máxima verossimilhança do parâmetro deste modelo, mostrar todos os passos da solução.

Suponha que a variável aleatória tenha a seguinte função de densidade de probabilidade:

Seja uma amostra aleatória de tamanho . Ache o estimador de máxima verossimilhança do parâmetro .

Com intenção de estimar um parâmetro desconhecido, foram propostos inicialmente dois estimadores e que satisfazem e . Pode-se afirmar que um novo estimado vai ser tendencioso para estimar e que seu viéis será igual a .