Duas bolas são escolhidas aleatoriamente de uma urna que contém bolas brancas, pretas e laranjas. Suponha que ganhemos para cada bola preta selecionada e percamos para cada bola branca selecionada. Suponha que represente nossas vitórias. Qual são os valores possíveis de e quais são as probabilidades associadas a cada valor?
Passo 1
E aí.....tudo belezinha?
Nesse problema temos uma urna em que duas bolas são escolhidas aleatoriamente. Essa urna tem:
- bolas brancas.
- 4 bolas pretas.
- bolas laranjas.
Ganhamos para cada bola preta selecionada e perdemos para cada bola branca selecionada.
A partira daí temos que calcular a probabilidade de todos os possíveis valores que podemos ganhar ou perder no final das escolhas.
Tem ideia de como fazemos isso?
Para resolver esse problema podemos usar a fórmula da probabilidade clássica com as combinações das possibilidades.
Saca só!
Passo 2
A combinação total é a quantidade de bolas que podemos escolher nas duas jogadas.
Se temos bolas totais e escolhas, então:
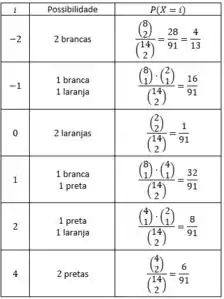
Se temos que escolher bolas, então as possibilidades de são:
Para , temos que a possibilidade de escolher duas brancas são:
Logo, é:
Para , temos que escolher uma bola branca e uma laranja, ou seja:
Então é:
Sacou como faz?
Veja só para os outros casos:
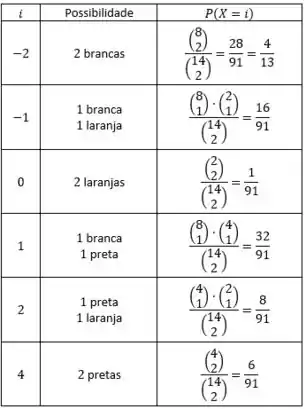
É isso! O que achou? Responde Aí!
Resposta