Durante as temporadas de 1999 e 2000 de beisebol , houve muita especulação de que o grande número , pouco comum , de corridas à base ( home runs ) executadas foi devido , no mínimo , em parte a uma bola com mais energia . Uma maneira de testar a " disposição de uma bola de beisebol é lançá - la em direção a uma superfície vertical . com uma ve locidade conhecida Ve medir a rarão da velocidade de saida V , da bola em relação a V. A razão R = V / V é chamada de coeficiente de restituição . A seguir , são apresentadas as medidas do coeficiente de restituição para 40 bolas de beisebol selecionadas aleatoriamente . As bolas foram arremessadas em direção a uma superficie de carvalho através de uma máquina de lançamento ,

( a ) Há evidencia que suporte a suposição de que o coeficiente de restituição seja normalmente distribuido ?

( b ) Encontre um IC de 99 % para o coeficiente médio de restituição

( c ) Encontre um intervalo de previsão de 99 % para o coeficiente de res . tituição para a próxima bola de beisebol que será testada .

( d ) Encontre um intervalo que conter : 99 % dos valores do coeficiente de restituição com 95 % de confiança

( e ) Explique a diferença entre os tres intervalos calculados nos itensib ( c ) e ( d ) .

Nos eixos horizontais estão os valores . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados desviarem significativamente da linha reta, o modelo hipotético não é apropriado.

Na forma descrita anteriormente, construímos um gráfico de probabilidade normal com base

nas observações

0,6248 0,6237, 0,6118 0,6159 0,6298 0,6102 0,6520 0,6368, 0,6220 0,6151 0,6121 0,6548 0,6226 0,6280 0,6096 0,6300 0,6107 0,6392 0,6230, 0,6131 0,6223 0,6297 0,6435 0,5978 0,6351 0,6275 0,6261 0,6262 0,6262 0,6314, 0,6128 0,6403 0,6521 0,6049 0,6170 0,6134 0,6310 0,6065 0,6214 0,6141

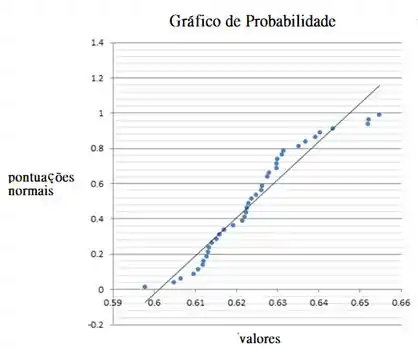
O gráfico de probabilidade normal não contém curvatura forte e o padrão é aproximadamente linear, então podemos concluir que os valores dos dados são aproximadamente normalmente distribuídos.

A média da amostra é:

O desvio padrão é:

Suponha que é uma amostra aleatória de uma população normal. Queremos prever o valor uma única observação futura. Uma previsão de é , a média da amostra.

Se e s são a média e o desvio padrão de uma amostra aleatória de uma distribuição normal com variância desconhecida , um intervalo de confiança em é dado por

onde, é o ponto percentual superior da distribuição t com n - 1 graus de liberdade.

Letra b:

Agora, precisamos encontrar um IC de 99% na média da população, então

Das equações, temos:

Portanto, um IC de 99% na média da população é

Um intervalo de predição (IP) de em uma única observação futura de uma distribuição normal é dada por

Letra c:

Sabemos que o nível de confiança é 99% e o tamanho da amostra é n = 40. Portanto,

Sabemos que o desvio padrão e a média da amostra , então da equação anterior, obtemos

Portanto, um intervalo de predição de 99% é

Um intervalo de tolerância para capturar pelo menos dos valores em uma distribuição normal com nível de confiança é

onde k é um fator de intervalo de tolerância encontrado na Tabela XII do Anexo. Os valores são dados para e e para e de confiança.

Letra d:

Primeiro, nós achamos o valor de k. Sabemos que o nível de confiança é 99% e , o tamanho da amostra é n = 40. Portanto, da Tabela XII do Apêndice, o valor de k é:

Agora, da equação, um intervalo de tolerância é

Letra e:

Da parte b), c) e d), concluímos que a duração do intervalo de tolerância é mais longo do que a duração do intervalo de predição e a duração do intervalo de predição é maior do que a duração do intervalo de confiança.