Uma empresa produtora de cimento, desejando abrir uma fábrica no Paraná, realizou um estudo da demanda do produto, com a finalidade de pleitar um empréstimo junto ao BNDE. Para isto, coletou dados sobre o consumo (expresso em 1.000 ton.), a renda “per capita” (expressa em Cr$) e o número de habitantes (expresso em milhares), referentes ao ano de 1968, para os 21 estados brasileiros. Feita a análise, verificou-se que a relação entre as variáveis assumia a forma funcional: , a qual recai em:

,

mediante as seguintes transformações logarítmicas:

, , e .

Tomados os logaritmos dos valores obtidos no levantamento, foram calculados:

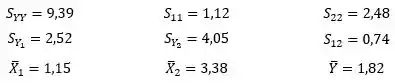
Pede-se:

1. Dar a equação da regressão de só em função de ;
2. Dar a equação de regressão de em função de e : ;
3. Calcular o coeficiente de explicação dessas 2 regressões;
4. Efetuar a análise do melhoramento do modelo múltiplo (com e ) em relação ao modelo simples (só com ), ao nível de 0,5%;
5. Calcular o consumo de cimento estimado, num estado em que a renda “per capita” é de Cr$ 200,00 e a população de 5.000.000 habitantes.

Já no item b) queremos a regressão de em função de e , onde:

Vamos calcular os valores de , e , através das equações:

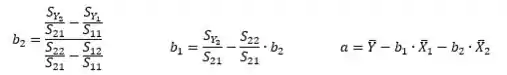
Logo:

Sabendo que (como visto no Passo 1):

Então temos a seguinte regressão:

No item c) iremos calcular o coeficiente de explicação pela seguinte equação:

Para a regressão de só em função de , temos a equação da seguinte forma:

Como visto no Passo 1, :

Já para a regressão de em função de e , iremos utilizar a equação inteira ( e ):

Para o item d) iremos realizar a análise de melhoramento. Essa análise tem como objetivo avaliar se o aumento de variáveis no modelo pode melhorar o mesmo de maneira significativa. Se o modelo é dado por , onde explica e acrescentamos outra variável explicativa no modelo, temos e a explicação é dada por . O melhoramento, devido a introdução de uma nova variável é dado pela equação:

E a tabela de Análise de Variância fica:

Se então o melhoramento é significativo.

Para este Passo iremos precisar do valor de estados brasileiros. Com isso, conseguimos encontrar o valor de tabelado, onde:

• ;
• .

Para :

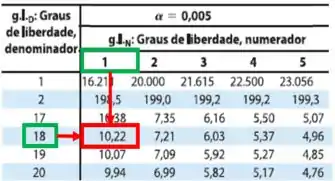
Agora vamos calcular o melhoramento:

E o quadrado médio residual:

Com isso conseguimos obter calculado:

Como (), o melhoramento é significativo para .

No item e) temos os seguintes dados:

• ;
• .

Com a equação que encontramos no Passo 2, conseguimos encontrar o consumo estimado de cimento:

Esse exercício foi demoradinho, mas espero ter conseguido te ajudar, até mais!