Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 6.Problemas - Ex. 25

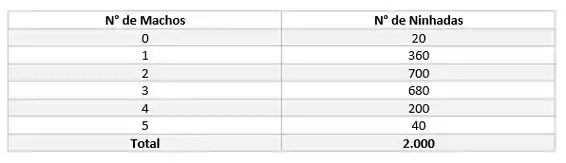
Examinaram-se 2.000 ninhadas de cinco porcos cada uma, segundo o número de machos. Os dados estão representados na tabela abaixo.

(a) Calcule a proporção média de machos.

(b) Calcule, para cada valor de X, o número de ninhadas que você deve esperar se X ~ b ( 5 , p ) , onde p é a proporção média de machos calculada em (a).

Passo 1

Primeiro precisamos calcular o número médio de machos por ninhada:

x - = ∑ i = 0 n x i n

Com esse valor médio usaremos a seguinte fórmula:

E X = x - = n p

Com isso, matamos a alternativa (a).

Na (b) usaremos a proporção calculada na (a), e jogaremos na fórmula de probabilidade da distribuição binomial para P(X=0), P(X=1), ..., P(X=5).

P X = k = n k   p k q n - k ,   k = 0 ,   1 ,   2 ,   … ,   n

Por fim, para calcularmos o número esperado de ninhadas para cada valor de X, se X ~ b ( 5 , p ) , basta multiplicarmos o total por cada probabilidade encontrada, ou seja,

2000 × P ( X = k )

Agora que já sabemos como resolver, partiu?

Passo 2

Calculando o número médio de machos por ninhada:

x - = 0 × 20 + 1 × 360 + 2 × 700 + 3 × 680 + 4 × 200 + 5 × 40 2000 = 2,4

Mas x - = 5 × p → p = 0,48

Passo 3

Agora vamos matar a alternativa (b) com X ~ b 5 ; 0,48

P X = 0 = 5 0   p 0 q 5 = 0,0380

Já o número esperado de ninhadas será

2000 × 0,0380 = 76

Faremos isso até P ( X = 5 ) , certo?

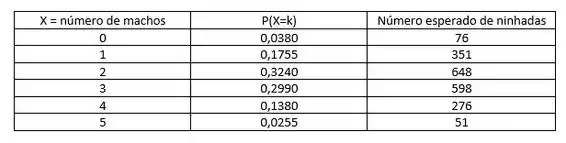
Você pode deixar a sua resposta final assim, ou se tiver tempo, arrumar numa tabela maneira como essa:

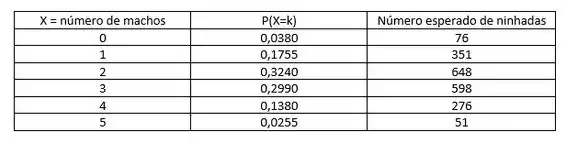
Resposta

(a) p = 0,48

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sendo X uma variável seguindo o modelo Binomial com parâmetros n = 15 e p = 0,4 ; pergunta-se: P ( X ≥14 ) . P ( 8X ≤ 10 ) . P ( X2o uX ≥11 ) . P ( X ≥ 11o uX13 ) . P ( X3eX6 ) . P X ≤ 13 X ≥ 11 ) .
Em treinamento de animais, usa-se a repetição como estratégia de aprendizagem. Num experimento, um macaco realiza certa tarefa corretamente, pela primeira vez, com probabilidade 0,5. Caso falhe, a pro
Um time paulista de futebol tem probabilidade 0,92 de vitória sempre que joga. Se o time atuar 4 vezes, determine a probabilidade de que vença:Todas as 4 partidasExatamente 2 partidas.Pelo menos uma p
Uma vacina contra a gripe é eficiente em 70% dos casos. Sorteamos, ao acaso, 20 dos pacientes vacinados e pergunta-se a probabilidade de obter:Pelo menos 18 imunizados.No máximo 4 imunizados.Não mais
A resistência (em toneladas) de vigas de concreto produzidas por uma empresa, comporta-se conforme a função de probabilidade abaixo:Admita que essas vigas são aprovadas para uso em construções se supo