Exercícios de Distribuição de Bernoulli e Binomial - Lista de Exercícios Resolvida

Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:

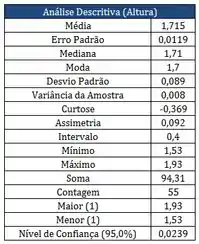
Dados Pareto:

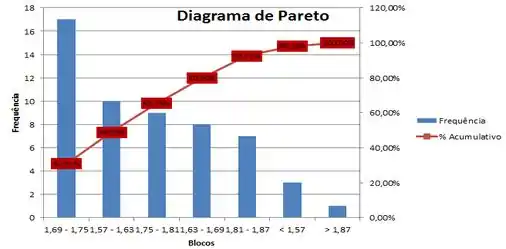
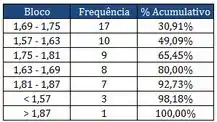
1. Se a probabilidade de um aluno de probest faltar à aula é de 5% e supondo que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?

Estabeleça as condições exigidas para se aplicar a distribuição binomial?

Qual é a probabilidade de 3 caras em 5 lançamentos de uma moeda honesta?

Qual é a probabilidade de menos que 3 caras em 5 lançamentos de uma moeda honesta?

Se , sabendo-se que e determinar:

a) n

b) p

c)

d)

e) E(Z) e Var(Z), onde

f) , onde

g), onde

Em um pequeno restaurante gourmet existem mesas para os seus clientes. Com base no que se vem observando, a gerência sabe que, todos os dias, as mesas serão reservadas e que a chance de comparecimento de alguém que tenha reservado uma mesa é sempre igual a uma mesma constante O comparecimento de qualquer cliente é independente do comparecimento dos demais. A distribuição acumulada de , número de clientes com reserva que comparecem, é:

(b)

Qual é o valor de ?

(c)

Qual a probabilidade de que, durante os dias de um fim de semana de trabalho, em exatamente desses dias todos os clientes que fizeram reservas compareçam?

Em um histórico de provas P1 de PROBEST sabe-se que dos alunos faltam no dia da prova. O professor decide fazer a prova em uma sala onde tem lugares e a turma para fazer a prova é de alunos.

Qual a probabilidade de que não haverá lugar suficiente para todos os alunos?

Suponha que um experimento biológico deva ser repetido no mínimo vezes com sucesso para que seja validado. A cada dia só se pode realizar um experimento, que, em função de variações das condições do meio pode resultar em erro, anulando completamente tal tentativa. A chance de um experimento chegar até o fim sem sucesso é conhecida e igual a . O pesquisador trabalhará todos os dias, inclusive finais de semana e feriados até validar o seu experimento.

a) Identifique o modelo probabilístico que modela a chance do experimento ser validado em 𝑥 dias e apresente o valor esperado do número de dias que ele trabalhará.

b) Qual a probabilidade do pesquisador validar o seu experimento em exatos dias?

c) Qual a chance dele demorar mais que 6 dias para validar o experimento?

A tabela abaixo corresponde à análise descritiva das alturas dos alunos matriculados na disciplina PROBEST-2013-2 turma 3VB.

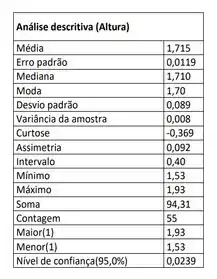
Usando os dados apresentados, pede-se:

a) Se a probabilidade de um aluno de PROBEST faltar à aula é de 4% e supondo que os alunos faltem às aulas de maneira estatisticamente independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula? b) E de comparecer mais de 52 alunos?

Suspeita-se que o processo de produção de certo tipo de componente esteja desregulado. Para decidir sobre a medida a ser tomada para sanar o problema, o departamento de produção resolveu conduzir um experimento em que 10 componentes serão sorteados ao acaso da linha de produção. Seja X o número de componentes fora das especificações entre eles. Considerando que a proporção de componentes fora das especificações na linha de produção como um todo seja de 30%:

a) Qual o valor mais provável de X e qual sua probabilidade?

b) Admitindo que:

- Se X ≥ 5, será efetuado um gasto total de 1000 reais para aprimorar a qualidade da produção.

- Se 2 ≤ X ≤ 4, esse gasto será de 300 reais.

- Se X ≤ 1, não será efetuado nenhum gasto.

Qual é o valor do gasto médio a ser efetuado?

A função de distribuição acumulada da Binomial(10;0,3) é fornecida, para facilitar os cálculos:

Retiram-se cartas, ao acaso e com reposição, de um baralho de cartas. Seja a variável aleatória definida como o número de reis na amostra.

1. Obtenha a função de probabilidade de e faça um gráfico da sua função de distribuição acumulada.
2. Obtenha a esperança e a variância de .

Sabe-se que um famoso atleta olímpico de tiro com arco costuma acertar o alvo na mosca em cerca de oito em cada dez vezes sob algumas condições específicas. Em um grande torneio internacional, em que estas mesmas condições acontencem, o atleta precisa acertar pelo menos duas vezes na mosca, em três tentativas, para ir às finais.

1. Sabendo que a acurácia dos tiros não se altera, proponha um modelo para a variável aleatória que representa o número de acertos na mosca e calcule a probabilidade do atleta ir às finais.
2. Determine os valores da função de distribuição acumulada da variável aleatória definida no item anterior para valores do argumento pertencente aos intervalos , , , e . Forneça uma representação gráfica desta função.

Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:

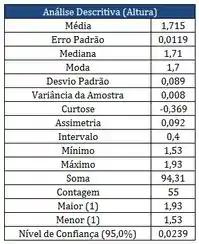
Dados Pareto:

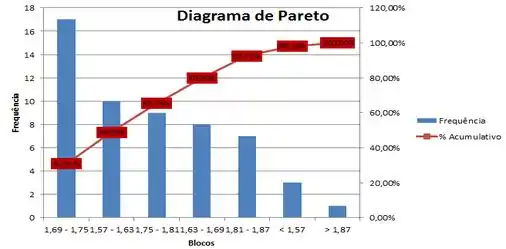
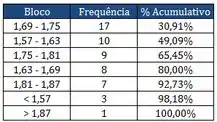
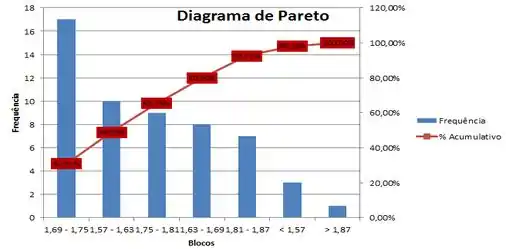
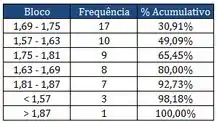
1. Através dos dados apresentados pelo Diagrama de Pareto, construa o Diagrama de frequência e o Histograma (Esboce Gráficos de Frequência e % Cumulativo).
2. Qual a quantidade de alunos com altura menor ou igual a 1,75?
3. Qual a quantidade de alunos com altura maior que 1,81?
4. Com relação à curtose, que tipo de curva podemos verificar? Por quê?
5. Quais são as medidas de Dispersão?
6. Se a probabilidade de um aluno de probest faltar a aula é de 5% e, suponha que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?

Em um histórico de provas P1 de PROBEST sabe-se que dos alunos faltam no dia da prova. O professor decide fazer a prova em uma sala aonde tem lugares e a turma para fazer a prova é de alunos.

Qual a probabilidade de que não haverá lugar suficiente para todos os alunos?

Dois times de futebol, e com nível técnico idêntico, ou seja, as chances de vitória de qualquer um deles e ocorrer um empate entre eles é a mesma. Estes dois times jogam entre si vezes (jogos). Encontre a probabilidade do time :

1. Ganhar dois ou três jogos?
2. Ganhar pelo menos um jogo?

Você está procurando emprego e está enviando seu CV (Currículo Vitae). Apenas dos CVs enviados resultam numa entrevista. Calcule as seguintes probabilidades:

Você manda exatamente CVs, qual a probabilidade de ser chamado para entrevistas?

Você manda CVs. Qual a probabilidade de ser chamado para menos de entrevistas?

Seja uma variável aleatória com distribuição Binomial cuja função de distribuição acumulada é dada por:

Determinar:

1. O valor da constante
2. Coeficiente de variação de
3. e

Uma empresa faz transporte de material por meio de caminhões e o volume de encomendas que ela recebe oscila ao longo do tempo. Admita que, escolhendo ao acaso um dia de trabalho:

• O número de entregas a serem feitas segue uma distribuição de Poisson com média de 5 entregas/dia;

• A empresa pode contratar, por empreitada, trabalhadores autônomos que constam de uma lista de 6 nomes. Todos eles tem a mesma chance de virem a ser contratados para servir à empresa naquele dia, e há independência entre as decisões de se contratar ou não relativas aos diversos trabalhadores da lista;

• O número de caminhões usados para realizar os serviços naquele dia pode ser igual a: 1 (com probabilidade 0,15), 2 (com probabilidade 0,60), ou 3 (com probabilidade 0,25).

Pergunta-se:

(b) Quais são os valores possíveis de , se a probabilidade de serem recrutados exatamente 3 empregados da lista de 6 é igual a 0,27648?

Dois times de futebol A e B com nível técnico idêntico, ou seja, as chances de vitória de qualquer um deles ou de acontecer um empate entre eles é a mesma. Estes dois times jogam entre si vezes (jogos). Pela identificação do modelo probabilístico que modela a chance do experimento ser validado em jogos, encontre a probabilidade do time A de:

a) Ganhar dois ou três jogos?

b) Ganhar pelo menos um jogo?

A variável aleatória (v.a.) segue um modelo Binomial com parâmetros e .

a) Se e , calcule .

b) Se e , calcule o valor de .

c) Se e , calcule o valor de .

d) Se e , determine os valores de e .

Em um determinado jogo, um jogador vendado tem direito a escolher 5 cartas em um baralho contendo 8 cartas douradas e 12 cartas brancas. Cada vez que uma carta é escolhida, verifica-se a sua cor e ela é devolvida ao baralho, que é embaralhado. Cada carta dourada que o jogador tira rende-lhe um prêmio de R$ 100,00.

1. Quanto se espera que o jogador ganhe, em média, neste jogo? Qual é o desvio padrão do prêmio do jogador?
2. Qual é a probabilidade de que o jogador ganhe algo?
3. Qual é a probabilidade condicional de que o jogador ganhe o prêmio máximo, dado que ele ganhará algo?

03) Um plantador de cocos divide sua fazenda em lotes de para efetuar o plantio rotativo. Ele tem lotes de coco no total. Todo mês ele colhe cocos de lotes onde os cocos já estão maduros. Em dos lotes de plantas maduras, em média, ocorrem pragas e os cocos não podem ser colhidos. Qual a probabilidade de em mês não conseguir colher os cocos em apenas dos lotes?

A)

B) 2/50

C)

D)

E)

13) Sabe-se que apenas dos alunos da disciplina de Probabilidade compram o livro-texto enquanto usam livros da biblioteca e/ou estudam apenas por notas de aula e materiais disponíveis no Moodle. Foram selecionados aleatoriamente alunos da disciplina. A probabilidade de que o número de alunos que compram o livro-texto dentre os selecionados seja maior que desvios-padrões acima de seu valor médio é (lembre-se: desvio padrão é a raiz quadrada da variância):

A)

B)

C)

D)

E)

Em um histórico de provas P1 de PROBEST sabe-se que 3% dos alunos faltam no dia da prova. O professor decide fazer a prova em uma sala aonde tem 58 lugares e não tem espaço para colocar mais carteiras, e a turma para fazer a prova é de 61 alunos.

Qual a probabilidade de que não haverá lugar suficiente para todos os alunos?

Em um pequeno restaurante gourmet existem mesas para os seus clientes. Com base no que se vem observando, a gerência sabe que, todos os dias, as mesas serão reservadas e que a chance de comparecimento de alguém que tenha reservado uma mesa é sempre igual a uma mesma constante O comparecimento de qualquer cliente é independente do comparecimento dos demais. A distribuição acumulada de , número de clientes com reserva que comparecem, é:

1. Ache a função de probabilidade de , e .
2. Qual é o valor de ?
3. Qual a probabilidade de que, durante os dias de um fim de semana de trabalho, em exatamente desses dias todos os clientes que fizeram reservas compareçam?

Seja uma v.a. com distribuição de Bernoulli com parâmetro . Mostre os passos necessários que provem que e

Você está procurando emprego e está enviando seu CV (Currículo Vitae). Apenas dos CVs enviados resultam numa entrevista. Calcule as seguintes probabilidades:

b) Você envia exatamente 15 CVs, qual a probabilidade de ser chamado para 2 entrevistas?

c) Você envia exatamente 30 CVs, qual a probabilidade de ser chamado pelo menos para 3 entrevistas?

Um supermercado faz a seguinte promoção: o cliente, ao passar pelo caixa, lança um dado honesto. Se sair face “6" ele ganha um desconto de 30% sobre o total de sua compra. Se sair face “5", o desconto é de 20%. Se sair face “4", o desconto é de 10% e, se sair faces “1", “2" ou “3", o desconto é de 5%. Seja a variável aleatória definida como o desconto concedido ao cliente na promoção. Pede-se:

1. a função de probabilidade da variável aleatória ;
2. o desconto médio concedido na promoção;
3. a probabilidade de que num grupo de 5 clientes, pelo menos um obtenha um desconto maior do que 10%.

Suponha que um experimento biológico deva ser repetido no mínimo 4 vezes com sucesso para que seja validado. A cada dia, só se pode realizar um experimento, que, em função de variações das condições do meio pode resultar em erro, anulando completamente tal tentativa. A chance de um experimento chegar até o fim sem sucesso é conhecida e igual a 68%. O pesquisador trabalhará todos os dias, inclusive finais de semana e feriados até validar o seu experimento.

a) Identifique o modelo probabilístico que modela a chance de o experimento ser validado em dias e apresente o valor esperado do número de dias que ele trabalhará.

b) Qual a probabilidade de o pesquisador validar o seu experimento em exatos dias?

c) Qual a chance de ele demorar mais que dias para validar o experimento.

Uma empresa aérea sabe que 15% das pessoas que fazem reservas aéreas cancelam suas reservas.

A empresa vende 60 passagens para um voo que contém apenas 56 lugares. Supondo que as pessoas cancelam suas reservas de maneira independente, calcule a probabilidade de que haverá assentos para todos os passageiros.

Suponha que a probabilidade de os pais terem um filho(a) com cabelos loiros seja . Se houverem crianças na família, qual é a probabilidade de que metade delas tenham cabelos loiros?

Dois times de futebol A e B com nível técnico idêntico, ou seja, as chances de vitória de qualquer um deles ou de acontecer um empate entre eles, é a mesma. Estes dois times jogam entre si 6 vezes (jogos). Pela identificação do modelo probabilístico que modela a chance do experimento ser validado em jogos, encontre a probabilidade do time A de:

1. Ganhar dois ou três jogos?
2. Ganhar pelo menos um jogo?

Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:

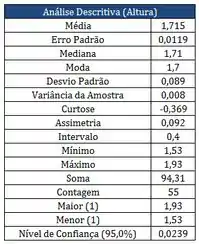
Dados Pareto:

1. Se a probabilidade de um aluno de probest faltar à aula é de 5% e suponde que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?

Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).

Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).

Em um determinado período do dia constatou-se que existem somente 20 vagas livres e que nenhum carro iria sair por se tratar de horário de prova. Vinte carros estão na fila para entrar. Qual a probabilidade de menos que 2 carros desta fila serem placa final igual a 3?