Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 16
A função de probabilidade conjunta das variáveis X e Y é dada pela seguinte tabela de dupla entrada.
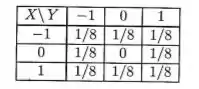
- Verifique se
- X e Y são independentes? Comente.
Passo 1
Vamos montar uma tabela de XY e também a sua função de probabilidade, assim:
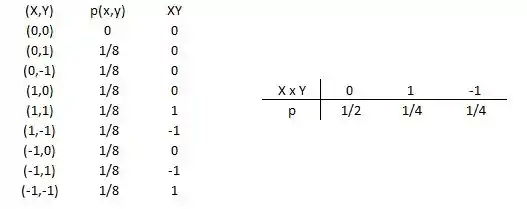
Temos que a esperança é dada por:
Assim, teremos que:
Fazendo a função de probabilidade das marginais de X e Y, teremos:
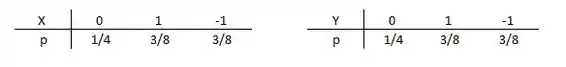
Daí, suas esperanças serão:
Daí, podemos dizer que , pois:
Passo 2
Não podemos afirmar que elas são independentes por . Pois o que vale é, se as variáveis são independentes então por , mas não ao contrário.
Assim, vamos montar a tabela de dupla entrada com as marginais, para verificarmos se são ou não independentes, daí:
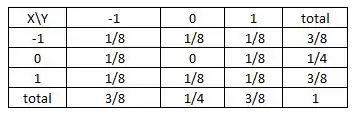
Observe que, ao fazermos , assim, provamos que elas não são independentes.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja X a variável aleatória do problema 6.7.Determine a fgm de X, ache E(X) e V(X).
Suponha que a fgm da variável aleatória X seja da forma M x t = 0,4e t + 0,6 8 Qual será a fgm da variável aleatória Y = 3 X + 2 ? Calcule E(X).
Seja X o resultado da jogada de uma moeda equilibrada:Determine a fgm de X, ache E(X) e V(X).
Em um circuito, n resistores são montados em série. Suponha que a resistência de cada um seja uniformemente distribuída sobre [0,1]e suponha, também, que todas as resistências sejam independentes. Sej
Empregue a fgm para mostrar que, se X e Y forem variáveis aleatórias independentes, com distribuição N ( μ x , σ x 2 ) e N μ y ,σ y 2 , respectivamente, então Z = a X + b Y será também normalmente dis