Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 4.Exercícios - Ex. 45

Suponha que X seja distribuída normalmente, com uma media de 10 e um desvio-padrão de 2. Determine o seguinte:

  1. P ( X < 13 )
  2. P ( X > 9 )
  3. P ( 6 < X < 14 )
  4. P ( 2 < X < 4 )
  5. P ( - 2 < X < 8 )

Passo 1

Seja X a variável aleatória normal com a média de 10 e desvio padrão 2.

Em seguida, introduzimos a variável aleatória Z da seguinte forma:

Z = X - 10 2

Z é a variável aleatória normal padrão com a função de distribuição cumulativa Φ dada nas tabelas dos apêndices do livro.

Passo 2

Na letra a:

P ( X < 13 ) = P ( X - 10 2 < 13 - 10 2 ) = P ( Z < 1.5 ) = Φ ( 1.5 ) = 0.933

Passo 3

Na letra b:

P ( X > 9 ) = P ( X - 10 2 > 9 - 10 2 ) = P ( Z > - 0.5 ) = 1 - Φ ( - 0.5 ) = 0.69

Passo 4

Na letra c:

P ( 6 < X < 14 ) = P ( - 2 < X - 10 2 < 2 ) = 2 Φ ( 2 ) - 1 = 0.9545

Passo 5

Na letra d:

P ( 2 < X < 4 ) = P ( - 4 < X - 10 2 < - 3 ) = Φ ( 4 ) - Φ ( 3 ) = 0.00135

Passo 6

Na letra e:

P ( - 2 < X < 8 ) = P ( - 6 < X - 10 2 < - 1 ) = Φ ( 6 ) - Φ ( 1 ) = 0.16

Passo 7

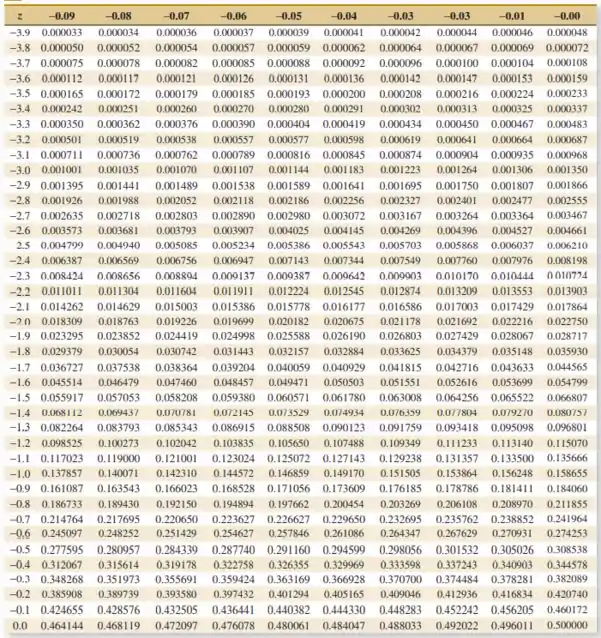
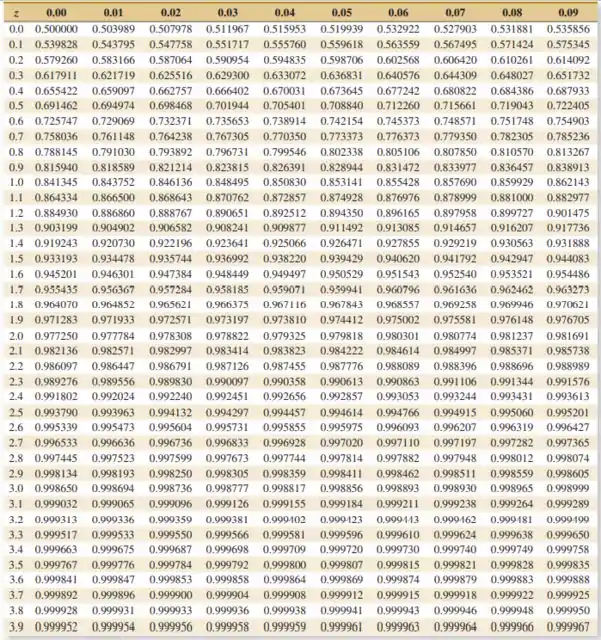
Resposta

  1. 0.933
  2. 0.69
  3. 0.9545
  4. 0.00135
  5. 0.16
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As vendas de determinado produto têm distribuição aproximadamente normal, com média 500 unidades e desvio padrão 50 unidades. Se a empresa decide fabricar 600 unidades no mês em estudo, qual é a
De um lote de produtos manufaturados, extraímos 100 itens ao acaso; se 10% dos itens do lote são defeituosos, calcule a probabilidade de 12 itens serem defeituosos. Use também a aproximação norma
Suponha que as amplitudes de vida de dois aparelhos elétricos, D1 e D2, tenham distribuições N(42, 36) e N(45, 9), respectivamente. Se os aparelhos são feitos para ser usados por um período de 45
As alturas de 10.000 alunos de um colégio têm distribuição aproximadamente normal, com média 170 cm e desvio padrão 5 cm.(a) Qual o número esperado de alunos com altura superior a 165 cm?(b) Qu
Para a v.a. X ~ N(μ, σ 2), encontre:(a) P(X ≤ μ+2σ),(b) P(|X–μ|≤ σ),(c) o número a tal que P(μ – aσ ≤ X ≤ μ + aσ) = 0,99, (d) o número b tal que P(Xb) = 0,90.