Para uma variável aleatória com densidade Normal e desvio padrão 5, o teste da média , teve a região crítica dada por para uma amostra de tamanho 25. Determine as probabilidades de erros tipo .
Passo 1
Antes de mais nada, seja a nossa variável com distribuição .
Perceba então que temos um caso de teste para a média com variância conhecida; nesses casos vamos utilizar a seguinte aproximação:
Além disso, temos a seguinte região crítica:
E estamos testando as seguintes hipóteses:
Lembrando que rejeitamos quando pertencer à RC.
Passo 2
Agora, lembrando que o erro tipo é a probabilidade de a gente rejeitar sendo que ela é verdadeira.
Em outras palavras:
Ou seja,
Vamos usar a aproximação pela normal padrão para encontrar as chances de cometer esse erro:
E então:
Lembrando que o gráfico de um modelo normal é simétrico, podemos dizer o seguinte:
E
Obs: isso é possível pois a tabela nos da as probabilidade sempre de .
Vamos buscar na tabela então:
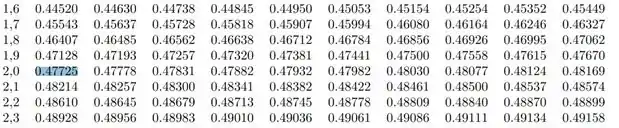
Portanto
Isso significa que a nossa chance de cometer erro tipo é:
Passo 3
Já o erro tipo , é o contrário; ou seja, é a probabilide de aceitarmos a hipótese nula, sendo ela falsa.
Como rejeitamos se pertencer à zona crítica, então aceitamos caso não pertença a RC; em outras palavras:
Novamente fazendo a aproximação:
Agora, queremos:
Como o gráfico é simétrico:
É exatamente igual ao erro (somente neste caso).
Portanto
Resposta
Concluimos então: