Teste de Aderência
Produzido por Jorge Alberto NascimentoTeoria
O teste de aderência nos diz se a distribuição dos dados é semelhante à uma distribuição de referência!
-Hãam? 😖
Vem comigo que tudo vai ficar mais claro! E pra começar, a gente vai fazer de conta que lançamos uma moeda
Distribuição Qui-quadrado
A Distribuição qui-quadrado
-Mas como eu posso saber se a moeda esta viciada? 😖
Usando a distribuição Qui-Quadrado juntamente com o teste de aderência! 🤩
Na prática usamos uma tabelinha com essa cara aqui:
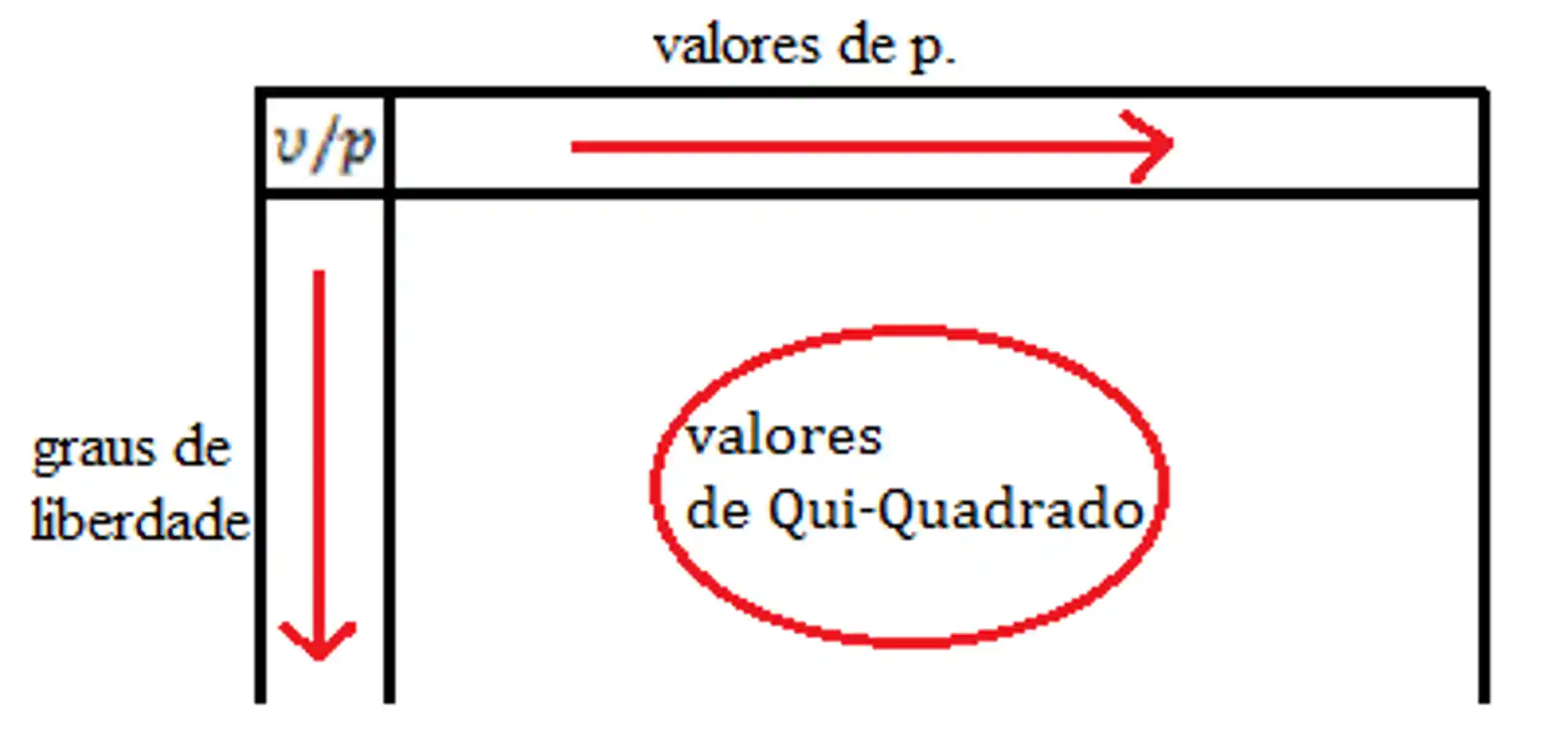
Onde:
de graus de liberdade nível de confiança
📢 Clique para ver mais:
- Teste de Aderência: Exercícios Resolvidos
- Teste de Hipótese
- Tabela Distribuição Normal
- População e Amostra
Como Fazer o Teste de Aderência
No teste de aderência a gente vai ver se o número de vezes que uma situação ocorre tá dentro do previsto pelo modelo teórico! Para isso, vamos usar o teste de hipótese. Mas, qual deve ser a hipótese adotada?
Nós queremos que as probabilidades observadas sejam iguais as probabilidades esperadas, ou, pelo menos, bem próximas. Então, tomamos como hipótese
Onde:
é a probabilidade observada para o valor i; é a probabilidade esperada para o valor i; é o número de casos possíveis.
Onde
Você também pode conferir esse conteúdo em vídeo:
Exemplo: Uma moeda foi lançada 100 vezes, verifique se essa moeda é viciada
Pra começar, precisamos dos dados:
lançamentos; resultados possíveis, que são cara e coroa; caras; coroas; de significância;
Aplicando o teste:
Agora olhando o quantil da 95% da qui-quadrado com 1 g.l.:
Como
Agora vamos praticar com exercícios?