Cinética dos gases
Produzido por Juliana EcheniqueTeoria
Já vimos que a pressão e o volume de um gás dizem bem mais do que a pressão e o volume de um líquido ou de um sólido, não é? Através da lei dos gases ideais, conseguimos relacionar essas grandezas físicas com a quantidade de moléculas do gás (o número de mols)...
Mas podemos ir além e relacionar essas grandezas com a velocidade das partículas do gás!
Teoria cinética dos gases
Essa teoria é toooda baseada em observações experimentais! Não vale muito a pena explicar pedacinho por pedacinho porque na real o mais importante é saber aplicar! Depois de muiiitos experimentos, chegou-se nessa fórmula aqui:
Onde é a pressão, o volume, o número de mols e a massa molar do gás, que algumas pessoas preferem usar .
E essa
Ok, ela é uma velocidade um pouco mais complicada! Ela é a raiz quadrada da velocidade quadrática média (a gente usa RMS porque vem do inglês, root mean square), e é calculada por:
Onde é o número de partículas do gás.. Ou seja, ela faz uma espécie de média das velocidades das partículas.
Para um gás ideal, podemos rearranjar a equação lá de cima com e achar:
Onde é a temperatura, a constante universal dos gases e a massa molar do gás.
Observação: A é bem importante porque é com ela que calculamos a energia cinética das moléculas!
Observação 2: As unidades podem ser beeeeem complicadas nessa equação (já que tem raiz e a constante dos gases, que pode ter várias unidades diferentes). Então, pra facilitar a sua vida, continua sempre no SI:
E isso vale pra qualquer gás em qualquer situação?
Esse modelo só funciona se levarmos em conta algumas hipóteses:
- As moléculas de um gás são muiiito pequenas e estão bem afastadas umas das outras, só interagindo quando colidem;
- Elas estão em movimento aleatório contínuo, se movendo em linha reta;
- Elas só trocam de direção/param quando colidem ou com outras moléculas, ou com o recipiente;
Mais ou menos como na figura:
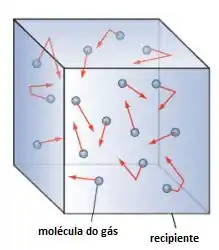
Ok, agora vamos praticar pra fixar essas informações?? 😊
E isso vale pra qualquer gás em qualquer situação?
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercícios de Física 2 - UFPB
(Adaptada) O gás hélio, com massa molar de 4 g/mol, a 330 K tem raiz quadrada da velocidade quadrada média molecular igual a . Qual a raiz quadrada da velocidade quadrada média molecular do oxigênio, com massa molar 32 g/mol, a essa temperatura?
Passo 1
A raiz quadrada da velocidade quadrática média é calculada pela fórmula:
Se o oxigênio e o hélio estão nas mesmas condições, é o mesmo em ambos os casos. Podemos então relacionar a velocidade do hélio com a velocidade do oxigênio segundo a fórmula:
Logo,
Passo 2
Outro jeito de calcular é substituindo direto os valores na fórmula, sem tentar relacionar com a velocidade do Hélio:
OBS: Pode haver diferença nos dois jeitos por conta do arredondamento nas raízes! Aqui, para bater, desconsiderei as casas decimais na conta final! Mas de qualquer jeito, mesmo com as diferenças decimais, os dois jeitos estão certos 😊
Resposta
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp168-Exercício 4.81
A raiz quadrada das velocidades quadráticas médias das moléculas do gás metano, , em uma dada temperatura é . Qual é a raiz quadrada das velocidades quadráticas médias dos átomos de criptônio na mesma temperatura?
Passo 1
Podemos calcular a raiz quadrada das velocidades quadráticas médias a partir da fórmula:
Como os dois estão nas mesmas condições, é igual para os dois!
Então, podemos relacionar os dois:
Aí vamos ter que dar um pulinho lá na tabela periódica (ou na Wikipedia mesmo) pra dar uma conferida na massa moalr do . Ou pega o spoiler na próxima linha.
Então:
Resposta
Exercício Resolvido #3
Adaptada de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 167-Exercício 4.79
Calcule as raízes quadradas das velocidades quadráticas médias das moléculas de:
a) metano
b) etano
c) propano
em
Passo 1
Para calcular as vamos usar a fórmula:
Pra essa galera, a única coisa que vai mudar e a massa molar do composto, nosso .
Vamos usar o no SI e a também, em .
Então bora lá.
Passo 2
a) Para o metano, que tem
Passo 3
b) Para o etano, que tem
Passo 4
c) Para o propano, que tem
Resposta
Exercício Resolvido #4
Lista de Exercícios - Prof. Jason Gallas, DF–UFPB
(a) Encontre a velocidade quadratica média do gás nitrogênio à .
(b) A que temperaturas a velocidade quadrática média será metade e o dobro desse valor?
Passo 1
a) Usando a fórmula que já tá ficando gravada no coração:
Sabendo que a massa molar do nitrogênio é e equivale a .
Passo 2
b) A metade da do item (a) é igual a . A temperatura correspondente será:
E o dobro da do item (a) é igual a . A nova temperatura será:
Resposta
a)
b) e
Exercício Resolvido #5
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp169-Exercício 4.110
Os air bags de automóveis contêm cristais de azida de sódio, , que, durante uma colisão, decompõem-se rapidamente para dar gás nitrogênio e o metal sódio. O gás nitrogênio liberado no processo infla instantaneamente o air bag. Suponha que o gás nitrogênio liberado se comporta como um gás ideal e que o volume dos sólidos produzidos é negligenciável (e pode ser ignorado).
a) Calcule a massa (em gramas) de azida de sódio necessária para gerar gás nitrogênio suficiente para encher um air bag de , em 1,37 atm e .
b) Qual é a raiz quadrada da velocidade quadrática média das moléculas do gás formadas?
Passo 1
a) Se considerarmos o um gás ideal, podemos calcular o número de mols de suficiente para encher o :
Para calcularmos a massa de azida de sódio, temos que usar a estequeometria da reação:
Como a proporção entre e é:
Como a massa molar de é :
Passo 2
b) Para calcular usamos:
Resposta
a)
b)
Exercício Resolvido #6
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp167-Exercício 4.77
Calcule a energia cinética molar (em joules por mol) de uma amostra de gás criptônio em:
a)
b)
c) A diferença de energia molar entre as respostas de (a) e (b) é a energia por mol necessária para elevar a temperatura do gás criptônio em . A quantidade é conhecida como capacidade calorífica molar. Quanto ela vale?
Passo 1
a) Para calcular a energia cinética molar, precisamos calcular a
E pra isso, precisamos da massa molar do Kr, que é .
Já que a temperatura nos foi dada com duas casas decimais, vamos utilizar a conversão mais “refinada”:
Como queremos a energia cinética molar, ou seja, de 1 mol, usamos a massa molar:
Passo 2
b) Mesma coisa da letra a, só muda a temperatura:
Passo 3
c) Ela vale:
Resposta
a)
b)
c)