Teoria
Opa, seja muito bem vindo ao Responde Aí! Bora conversar sobre os Gases Reais?
Gases Ideais
Os gases ideais são aqueles que seguem a lei dos gases ideais, também conhecida como a equação de Clapeyron:
Essa equação é bem famosa, mas ela só funciona em situações hipotéticas em que a pressão tende a zero, nesse caso a interação entre as moléculas gasosas praticamente não existe! Ou seja, os desvios da idealidade são causados pelas interações moleculares entre as partículas do gás!
📢 Clique para ver mais:
Fator de Compressibilidade (Z)
O fator de compressibilidade (Z) é um parâmetro fundamental para descrever o comportamento dos gases reais, pois indica a compressibilidade do gás em relação ao comportamento ideal. Ele pode ser calculado utilizando a seguinte fórmula:
Onde
- Se
as forças intermoleculares são principalmente repulsivas. Faz sentido, já que, como as moléculas se repelem, elas tendem a ficar mais afastadas – o que aumenta o volume molar. - Se
as forças intermoleculares dominantes são atrativas. Isso é, as moléculas se atraem e ficam mais juntinhas – diminuindo o volume molar.
O valor de
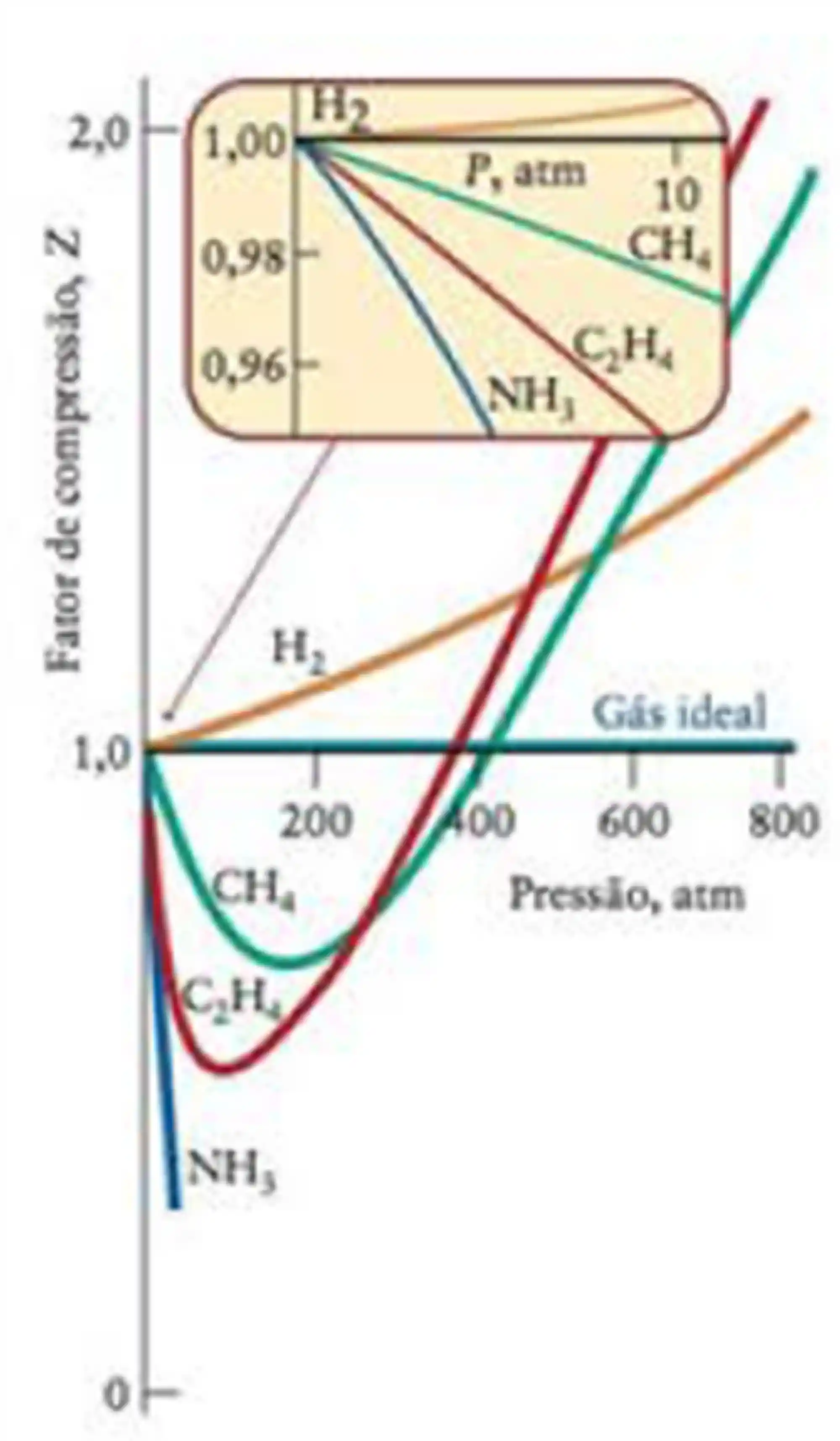
Como podemos ver nesse gráfico para o
Voltando para o gráfico: o caso do
Você também pode conferir esse conteúdo em vídeo:
Equação do Virial
A Equação do Virial é uma equação de estado que descreve o comportamento dos gases reais em termos de um somatório de termos que levam em conta as interações entre as moléculas.
Onde
Equação de Van der Waals
A Equação de Van der Waals é uma equação de estado que leva em conta o fato de que as moléculas dos gases reais têm volume próprio e interagem entre si, o que pode causar desvios das leis dos gases ideais em determinadas condições.
Os únicos elementos diferentes são o
Agora vamos praticar com exercícios?
Equação do Virial
Equação de Van der Waals
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercícios de Físico Química I – Instituto Federal de Educação, Ciência e Tecnologia RN
A e , o fator de compressibilidade do nitrogênio é . Calcular quantos quilogramas de nitrogênio serão necessários para encher um garrafão de nestas condições.
Passo 1
Vamos lá! Para calcular quantos kgs de vão ocupar nessas condições, precisamos calcular quanto um mol de ocupa não se comportando como gás ideal (já que ).
O fator de compressibilidade é definido por:
O volume molar ideal é tranquilo de calcular, já que é o volume que um mol de gás ocupa em certas condições de temperatura e pressão se considerarmos esse gás ideal!
Assim, podemos usar
Como:
Podemos escrever:
Passo 2
O então pode ser achado a partir da fórmula de !
Passo 3
Agora só calcular a massa pra preencher 1000L!
Como a relação volume – número de mols é:
A massa molar do é , logo:
Resposta
Exercício Resolvido #2
Lista de exercícios Físico-Química I – UFRGS
Um gás de van der Waals possui . A seu volume molar é igual a .
a) Calcule a constante
b) Qual o valor do fator de compressibilidade do gás nessas condições de temperatura e pressão?
Passo 1
a) Para calcular a constante vamos ter que usar a equação de van der Waals:
Vamos colocar todas as unidades no SI pra facilitar a vida, ein?
Relembrando rapidinho as unidades no SI:
Substituindo os valores...
Passo 2
Precisamos fazer uma análise dimensional, pra gente descobrir qual será a unidade de b, beleza?
Olha só, para eu conseguir somar e , preciso que:
Ok, agora voltando aos cálculos:
Passo 3
b) Para calcular o fator de compressibilidade, vamos usar sua fórmula:
Onde é o volume ocupado por um mol do gás quando ele se comporta como gás real e o volume ocupado por um mol do gás se ele fosse um gás ideal.
Nesse caso, o já temos: é dado no enunciado e é igual a .
Mas precisamos encontrar o podemos usar a lei dos gases ideais:
Passo 4
Agora que temos o volume molar ideal, podemos substituir esses dados na fórmula de Z, assim teremos:
Tranquilo?
Resposta
a)
b)
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp167-Exercício 4.91
Use a equação do gás ideal para calcular a pressão, em exercida por 1 mol de quando limitado ao volume de
a) ,
b) ,
c)
Repita os cálculos usando a equação de van der Waals. O que esses cálculos indicam sobre a precisão da dependência da pressão na lei dos gases ideais?
Dados: parâmetros de van der Waals do
Passo 1
Se o gás é ideal, vamos calcular sua pressão a partir da lei dos gases ideais, . Nesse caso, como só temos um mol de .
Para as 3 letras, só o que muda é o volume, então vamos calcular o numerador da fração antes:
Passo 2
Agora vamos resolver os itens.
a) Como estamos usando o R com essas unidades, precisamos usar o volume em (E a pressão vai sair em .
Assim...
Passo 3
b) Para :
Passo 4
c) Para :
Obs: faz sentido que a pressão aumente bastante quando diminuímos o volume, afinal as duas grandezas são inversamente proporcionais 😊
Passo 5
Usando a equação de van der Waals:
Podemos isolar a pressão e achar:
Vamos calcular as partes que não dependem do volume:
Com
Agora, para cada volume de (a), (b) e (c):
a)
b)
c)
Passo 6
O que a gente pode ver como diferença é que, quando as pressões são pequenas, existe pouca diferença entre os gases reais e gases ideais! Mas, conforme a pressão vai aumentando, as diferenças vão ficando beeem gritantes! E isso é o esperado, já que em grandes pressões fica mais difícil assumir que não existe interação entre as moléculas dos gases (o que daria a eles o comportamento de gases ideais).
Resposta
a)
b)
c)
Sobre altas pressões, o comportamento dos gases se diferencia muito do comportamento dos gases ideais.
Exercício Resolvido #4
Adaptada de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp169-Exercício 4.93
A tabela a seguir lista os parâmetros de van der Waals de . Use seu conhecimento dos fatores que governam as magnitudes de para atribuir a cada um desses quatro gases um valor de .
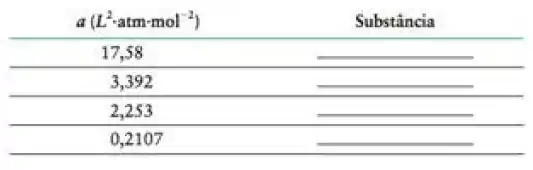
Passo 1
Como vimos durante o capítulo, o parâmetro de van der Waals é responsável pelas forças atrativas, enquanto o pelas forças repulsivas.
A substância que tem maior tem um maior desvio da idealidade por causa das forças atrativas!
Aí agora temos que analisar as interações intermoleculares que essas moléculas fazem entre si e analisar qual é mais forte entre elas... As moléculas que se ligam mais fortemente tem um maior desvio da idealidade por conta das forças atrativas 😊
Passo 2
Analisando as forças intermoleculares...
molécula apolar, faz dipolo induzido entre as moléculas..
: molécula polar (já que a ligação ) é super polarizada, faz dipolo-dipolo!
é um gás ideal, faz dipolo induzido também
também é uma molécula apolar e também faz dipolo induzido!
A partir dessa análise já sabemos que a molécula o gás com maior vai ser o já que suas moléculas interagem mais fortemente que as dos outros gases!
Passo 3
Agora que vem a maior dificuldade desse problema: diferenciar as moléculas que fazem dipolo-induzido!
O dipolo-induzido é uma diferença de cargas causadas pelos movimentos dos elétrons numa ligação. Essa diferença de cargas que fazem as moléculas se atrairem! Quanto maior a diferença de eletronegatividade entre os dois átomos da ligação, mais os elétrons vão preferir ficar “mais próximos” de um átomo do que de outro e mais dipolos vão ser criados!
Ou seja, as ligações mais polarizadas – com maior diferença de eletronegatividade – criam mais dipolos, o que facilita a ligação entre as moléculas.
Apesar de todas terem a mesma interação intermolecular, a molécula do é a que tem ligações mais polarizadas, já que a diferença de eletronegatividade do C e do O na ligação é bem grande. Ou seja, a possibilidade de se formar dipolos na molécula é beeem maior do que no por exemplo, que tem ligações bem menos polarizadas!
Assim, .
Passo 4
Já para o neônio, sua polarização é feita dentro do próprio átomo, com os elétrons que o orbitam! Complicado, né? Mas é só você pensar que quando existem dois átomos diferentes pra criar uma diferença de eletronegatividade fica mais fácil de criar pólos!
Assim,
Resposta
Exercício Resolvido #5
Lista de exercícios Professor Ricardo Freire – UFS
Se 1 mol de um gás ideal estivesse confinado em um volume de a , exerceria uma pressão de 1 atm. Use a equação de van der Waals e as constantes dadas neste exercício para estimar a pressão exercida por 1 mol de em .
Dados: parâmetros de van der Waals:
Passo 1
A equação de van der Waals é:
Temos todos os valores que precisamos, então só substituir na fórmula:
Ou seja, podemos ver que a pressão do gás real é menor do que a pressão do gás ideal!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Adaptada de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp167-Exercício 4.89
Dois balões idênticos estão cheios de um gás em e Um balão contém 1 mol de e o outro, 1 mol de
a) Em qual dos balões as moléculas tem maior raiz quadrada das velocidades quadráticas médias?
b) Em que balão a atração entre as moléculas é maior? Explique seu raciocínio e explique qual dos dois balões é esperado um maior desvio da idealidade.
Passo 1
a) Como vimos em cinética dos gases, a raiz quadrada média das velocidades, , é calculada por:
Onde M é a massa molar do gás!
Por essa fórmula, podemos ver que a massa molar e a são inversamente proporcionais, ou seja: quanto maior a massa molar, menor a !
Entre e , podemos concluir que a maior vai ser a do
Passo 2
b) A atração entre as moléculas é maior no balão em que os gases tem interações intermoleculares mais fortes! Entre o uma molécula apolar que faz dipolo-induzido, e o , que faz ligações de hidrogênio, o vai ter uma interação intermolecular muito maior do que no balão do
O maior desvio da idealidade é esperado no balão que tem as interações intermoleculares mais fortes, ou seja, no balão do .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. página 258 exercício 7.21
Em Termos da teoria cinética, como pode a velocidade de difusão de um gás ser afetada por um aumento na temperatura? Explique.
Passo 1
Como sabemos a raiz quadrada da velocidade quadrática média segue a seguinte equação:
Então a gente já vê que essa velocidade do gás aumenta de forma proporcional a raiz da temperatura. Então podemos esperar que gases aquecidos apresentam maior mobilidade, maior difusividade também, ou seja eles se espalham mais facilmente pelo espaço.
Passo 2
Quando a temperatura de um corpo é aumentada a energia absorvida pelas moléculas pode é convertida parcialmente em energia mecânica. Nesse caso parte dessa energia absorvida é convertda em energia cinética.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. página 258 exercício 7.23
Por que a pressão de um gás aumenta quando a temperatura aumenta, estando o volume constante?
Passo 1
Relacionar a velocidade com a temperatura
Como sabemos a raiz quadrada da velocidade quadrática média segue a seguinte equação:
Então a gente já vê que essa velocidade do gás aumenta de forma proporcional a raiz da temperatura
Passo 2
Agora vamos relacionar a pressão.
Seguindo a seguinte equação:
Com o aquecimento do gás o ganho de energia cinética das moléculas que ocorre resulta em um acréscimo no produto e nos casos em que o processo é isovolumétrico é constante o aumento da pressão deve compesar a estabilidade do
com da velocidade das moléculas o que ocorre com o acréscimo na temperatura naturalmente o produto tem que crescer também, estando o volume constante a pressão tem que aumentar.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. página 259 exercício 7.26
Que se entende por comportamento não ideal de um gás? Sob que condições esse comportamento é mais evidente?
Passo 1
Os gases ideais são formados de partículas com volume desprezível e que não sofrem interações intermoleculares, enquanto que na realidade as moléculas de gases ocupam um determinado volume e que a há possibilidade de haver interações intermoleculares.
Passo 2
O comportamento não ideal é mais evidente sob altas pressões, onde as interações entre as moléculas se torna mais relevante, exatamente devido à pressão, que “força as moléculas” a se aproximatem e interagirem.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #10
James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. página 259 exercício 7.28
Qual o significado físico das constantes a e b na equação de estado de Vander Waals para os gases reais?
Passo 1
A é um fator de correção que está relacionado a interações intermoleculares presentes no gás. Essas interações são responsáveis por reduzir a pressão que o gás efetivamente gera no sistema em relação ao previsto pela teoria dos gases ideais.
Passo 2
A constante b está relacionada ao volume das moléculas do gás. Imagine que as moléculas de gás dentro de um recipiente possam estar todas imóveis no fundo do frasco, é razoável prever que elas ocupariam um espaço no fundo do recipiente. O fator b está relacionado a esse volume. O produto “n.b” que a parece na equação de Van der Waals é chamado de volume excluído, ou seja, um volume que depende apenas do tamanho das moléculas e de sua quantidade e que é efetivamente incompressível.
Resposta
Ei, a resposta está no passo a passo :)