Introdução à termodinâmica
Teoria
Afinal, o que é termodinâmica?
E aí, tudo bom? 😊
A gente escuta bastante falar sobre termodinâmica e como ela é importante para a química, mas falta ainda uma definição, não é? Afinal, o que é a termodinâmica?
A termodinâmica é o estudo da energia: como ela pode ser transformada e transferida.
Para entendermos mais, vamos definir alguns conceitos fundamentais pra termodinâmica:
- Tipos de sistemas
- Transferência de calor e trabalho
- Calor específico e capacidade calorífica
Bora lá ver isso tudo então!
Sistemas e suas classificações
Vamos imaginar um bécher onde ocorre uma reação que queremos saber se é endotérmica ou exotérmica. Para isso, precisamos analisar a troca de energia da solução no bécher com o ambiente, certo?
O bécher, por ser nosso objeto de interesse de estudo, é chamado de sistema.
Já todo o arredor dele, o ambiente com o qual ele troca calor, é chamado vizinhança.
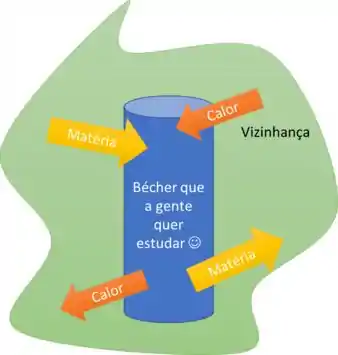
O conjunto sistema + vizinhança é muitas vezes chamado de universo.
Agora que sabemos que o sistema nada mais é que a parte específica do universo que desejamos estudar, podemos classificar esse sistema:
.
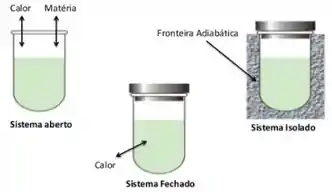
Obs: Fronteira adiabática, ou parede adiabática significa só que é uma fronteira que impede o calor de passar!
Aplicando no nosso exemplo do bécher:
- o bécher como sistema aberto seria ele em cima da bancada do laboratório, com a solução evaporando e a temperatura se igualando à temperatura externa.
- Já o sistema fechado aconteceria se vedássemos o bécher, e impedíssemos que a solução evaporasse. Assim, apenas a temperatura do bécher mudaria, até se igualar com a do ambiente.
- Para que o nosso bécher fosse um sistema isolado, precisaríamos vedá-lo e colocá-lo em um recipiente que evita a troca de calor, como uma garrafa térmica, por exemplo.
Transferência de energia: calor (q) e trabalho (w)
A gente sabe que se a gente encher nosso copo de refrigerante e demorar muito pra beber ele vai acabar esquentando. Assim, como se a gente demorar muito pra comer a comida esfria, certo?
Bom, o calor é a energia transferida quando há uma diferença de temperatura entre dois corpos. Então, assim como o refrigerante, quanto a comida quentinha, vão trocar calor com o meio ambiente até que as temperaturas se igualem.
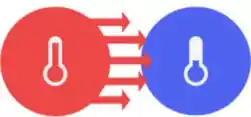
E como a energia existe na forma de calor, ela flui sempre do corpo mais quente para o mais frio.
Agora vamos pensar num outro caso!
Vamos pensar em um gás quente dentro de um recipiente, com um êmbolo em cima dele. Esse gás tem uma certa energia, e, ao se expandir e resfriar, ele empurra esse êmbolo móvel para cima.
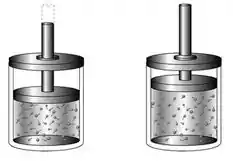
A energia necessária para empurrar esse pistão para cima é o trabalho!
Quando o gás se expande, então, ele aplica uma força contrária à força do pistão, para deslocá-lo, e assim realiza trabalho.
A definição de trabalho na física é a energia usada para deslocar um corpo contra uma força! Aqui na termodinâmica não é diferente!
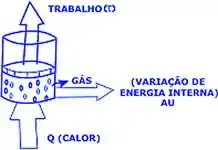
De uma maneira mais geral, energia é a medida da capacidade de um corpo de transferir calor ou realizar trabalho.
Um gás quente e comprimido tem mais capacidade de se expandir e realizar trabalho (levantando o êmbolo) do que um gás que já se expandiu e resfriou. Por isso o gás quente e comprimido tem mais energia do que o mesmo gás expandido e resfriado.
Energia interna
Como a gente falou então, a energia interna de um sistema é a energia total desse sistema, que pode ser convertida em calor ou em trabalho.
É beem complicado de calcular a energia por si só de um sistema, e o que mais nos interessa, na verdade, é como essa energia varia!
- Por exemplo: um gás que realiza de trabalho diminuiu sua capacidade de realizar trabalho em 20J, ou seja, diminuiu sua energia interna em . Ou seja, .
Agora, se por exemplo, a gente comprime esse gás, vamos estar realizando trabalho contra o sistema. Assim a gente aumenta a sua capacidade de se expandir (e realizar trabalho ele mesmo). Ai nesse caso a sua energia interna aumenta e o .
Com o calor não é muito diferente! Se o calor foi dado ao sistema, houve um aumento da sua capacidade de transferir calor e sua energia interna aumenta ().
Mas se o sistema perde calor, sua energia interna diminui ().
Capacidade calorífica
O calor é a energia consequente de uma diferença de temperatura, né? Mas o quanto de calor a gente tem que dar pra um sistema mudar a sua temperatura?
Calma! Já vou te explicar! Existe uma paradinha que se chama capacidade calorífica!
A capacidade calorífica de um corpo é uma propriedade que serve justamente para quantificar como esse calor fornecido/recebido altera a temperatura!
Ou seja, se um corpo tem uma alta capacidade calorífica, isso quer dizer que você pode fornecer bastante calor que a temperatura vai mudar pouco (já que e são inversamente proporcionais).
Já um corpo com uma baixa capacidade calorífica vai aumentar muiiito de temperatura com pouco calor fornecido.
Agora, um copo de água precisa de muito menos calor fornecido para aumentar do que uma piscina inteira.
A capacidade calorífica depende da massa do corpo, então a podemos definir 2 capacidades caloríficas para facilitar nossos cálculos:
Usando o calor específico de uma substância, podemos calcular o calor fornecido/recebido através da equação:
Obs: As unidades são beeem importantes pra você diferenciar o que é o que no rolê!
Guarda isso no seu coração, ok?
Por último, mas não menos importante... Como que a gente mede o calor específico de alguma coisa então?
Sem desespero, calorímetros são dispositivos que servem para quantificar o calor trocado e a variação de energia. Eles também usam a equação , mas nesse caso o é a capacidade calorífica do próprio calorímetro.
Bom, nesse tópico a gente viu bastante coisa e tem váaaarias situações que a gente usa a capacidade calorífica e os outros conceitos. Então não deixe de fazer os exercícios! Vamos praticar? 😊
Transferência de energia: calor (q) e trabalho (w)
Energia interna
Capacidade calorífica
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp280-Exercício 7.1
Identifique os seguintes sistemas como aberto, fechados ou isolados:
a) café em uma garrafa térmica de ótima qualidade;
b) liquido refrigerante na serpentina de uma geladeira;
c) um calorímetro de bomba no qual benzeno é queimado;
d) gasolina queimando em um motor de automóvel;
e) mercúrio em um termômetro;
f) planta viva.
Passo 1
Para resolver esse problema, precisamos lembrar a definição de cada tipo de sistema!
- Sistema aberto: há transferência de matéria e de calor.
- Sistema fechado: há transferência apenas de calor.
- Sistema isolado: não há tranferência nem de calor nem de matéria!
Agora vamos analisar as letras:
a) esse sistema café + garrafa térmica é um sistema isolado, pois a tampa evita que o café evapore e, portanto, evita a troca de matéria. Além disso, as paredes da garrafa térmica são feitas para imitar uma parede adiabática, ou seja, que não permite a troca de calor!
O esquema é assim:
Passo 2
b) Na serpentina da geladeira a ideia é justamente trocar calor! Mas a troca de matéria não acontece, então é um sistema fechado.
Passo 3
c) O calorímetro + benzeno queimando é um sistema isolado! Isso porque a ideia de fazer uma combustão no calorímetro é justamente conseguir controlar a quantidade de calor trocada. E esse calor só é trocado entre o calorímetro e o benzeno, e não com as vizinhanças.
Passo 4
d) Esse sistema é aberto! É um pouco intuitivo, já que sabemos que a queima de combustíveis libera pra atmosfera (ou seja, há troca de matéria). Além disso, é dessa queima que sai o calor necessário pro motor funcionar, então também há troca de calor.
Passo 5
e) O mercúrio em um termômetro é um sistema fechado, já que não há troca de matéria mas há troca de calor: a gente passa o calor pro mercúrio, que se expande de acordo com nossa temperatura corporal!
Passo 6
f) Um sistema aberto, já que a planta troca tanto matéria quanto calor com o ambiente o tempo todo!
Resposta
a) isolado
b) fechado
c) isolado
d) aberto
e) fechado
f) aberto
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 281-Exercício 7.19
Uma peça de cobre de massa 20 g, em , foi colocada em um recipiente isolado de capacidade calorífica desprezível, que continha 50,7 g de água em . Calcule a temperatura final da água. Suponha que não houve perda de energia para a vizinhança.
Dados:
Passo 1
Vamos lembrar a fórmula do calor recebido/fornecido por uma substância:
Nesse caso entre a água e o objeto de cobre, temos que todo o calor perdido pelo cobre será recebido pela água, já que o enunciado diz que não houve perda de energia para a vizinhança.
Vamos usar o calor perdido como negativo, valeu?
Além disso, temos a temperatura inicial tanto pro cobre quanto pra água. Mas não temos a temperatura final, que é exatamente o que queremos descobrir. A única coisa que sabemos, é que essa temperatura final será a mesma, tanto para o cobre quanto para a água.
Bora parar de papo e calcular isso aí?
Passo 2
Sabemos que:
Logo:
Substituindo o que temos:
Multiplicando os termos:
Isolando os termos com :
Prontinho! A temperatura final do sistema é de 24,7°C.
Passo 3
Tá vendo que a temperatura da água variou bem pouquinho, enquanto a do dobre variou pra caramba? Isso é porque o calor específico da água é grande quando comparado ao do cobre. Então ela precisa de muuuita energia pra variar sua temperatura 😉
Mais uma coisa: antes de sair substituindo tudo na fórmula, dá uma olhada se as unidades estão corretas, ok? Aqui tudo estava ok, por isso já saímos calculando 😉
Resposta
24,7 °C.
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp282-Exercício 7.21
A entalpia de combustão do ácido benzoico, que é muito usado para calibrar calorímetros, é . Quando 1,453 g de ácido benzoico foi queimado com um calorímetro, a temperatura aumentou . Qual é a capacidade calorífica do calorímetro?
Passo 1
Para resolvermos esse problema, precisamos lembrar das fórmulas que envolvem capacidade calorífica e temperatura:
- , onde C é a capacidade calorífica
- , onde c é o calor específico
Além disso, precisamos fazer uma análise do que acontece no calorímetro. Uma combustão é uma reação exotérmica, isso é, que libera calor... Esse calor que a reação libera é absorvido pelo calorímetro, e através da diferença de temperatura do calorímetro conseguimos quantificar esse calor.
Ou seja,
Onde o da reação ganhou aquele negativo porque a reação está “perdendo” calor, liberando energia, valeu?
Passo 2
Vamos começar calculando a energia liberada pela reação.
Quando reagimos um mol do ácido benzóico, o calor liberado é de 3227 kJ. Mas no enunciado, só queimamos 1,453 g, então temos que saber quantos mols estamos queimando.
Para isso, precisamos da massa molar dessa substância:
Onde 12 é a massa do carbono, 1 é a massa do hidrogênio e 16 é a massa do oxigênio.
Então, em 1,453g, temos:
E se 1 mol libera 3227 kJ de energia, 0,012 mol vai liberar:
Show, já sabemos que:
Passo 3
Agora vamos calcular o calor recebido pelo calorímetro.
Sabemos que:
Mas também sabemos que:
Como o enunciado nos deu que a temperatura do calorímetro aumento em 2,265°C:
Resposta
Exercício Resolvido #4
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.44
Dois objetos, A e B, são colocados em água fervente e deixados chegar à temperatura da água. Cada um é retirado e colocado em béqueres contendo 1000 g de água a . O objeto A aumenta a temperatura da água em ; o B aumenta a temperatura da água em .
a) Qual objeto tem a maior capacidade calorífica?
b) O que você pode dizer sobre os calores específicos de A e B?
Passo 1
a) Temos duas maneiras de responder essa questão, uma pensando no conceito de capacidade calorífica e outra usando as fórmulas!
- A capacidade calorífica mede quanto de calor eu preciso dar para um corpo para sua temperatura aumentar. Isso é, quanto maior a capacidade calorífica de uma substância, mais calor eu preciso ceder para que sua temperatura varie...
Agora vamos ver uma coisa. Quando colocamos os objetos A e B nos béqueres (com a mesma quantidade de água nos dois), o objeto A aumentou mais a temperatura da água (3,5 °C contra 2,6 °C). O que isso significa? Significa que ele liberou mais calor no meio!
Se ele liberou mais calor, podemos dizer que o objeto A tinha mais energia térmica que o objeto B.
Mas eles estavam, inicialmente, os dois na mesma temperatura (100°C, a da água fervente).
Se o objeto A estava na mesma temperatura que o objeto B mas tinha mais energia térmica, quer dizer que ele teve que absorver mais energia térmica pra chegar na temperatura de 100°C. Ou seja, ele tem maior capacidade calorífica.
Passo 2
Agora vamos resolver essa item a aí matematicamente.
A transferência de calor pode ser medida assim:
Igual a capacidade calorífica vezes o delt de temperatura.
E a gente pode abrir essa fórmula em:
Onde a gente troca a capacidade calorífica por massa vezes calor específico.
Sabendo que o calor específico da água é:
Vamos ver a quantidade de calor transferida do corpo A para a água:
Fazendo o mesmo para o béquer que recebeu B:
Mas a quantidade de calor que a água recebe do objeto A é igual a que A cede para a água. Então podemos escrever:
Fazendo o mesmo para B:
Note que a temperatura inicial dos dois objetos era 100°C porque estavam na água fervente. E, considerando que os corpos tinham atingido o equilíbrio térmico, no final eles estavam com a mesma temperatura da água nos seus respectivos béqueres. Logo:
Passo 3
b) O calor específico de uma substância pode ser calculado por:
Então, enquanto é uma característica do objeto, é uma característica da substância, dado em , ou equivalente. Ele indica o quanto precisamos dar a um grama de determinada substância para variar a temperatura dela em 1 °C.
Como não temos nenhuma informação sobre as massas de A e B, não podemos falar nada sobre suas capacidades caloríficas.
Pode ser, por exemplo, que os dois objetos sejam da mesma substância, logo, tenham mesmo . Mas se a massa de A for maior, ele vai precisar de mais energia pra ser aquecido e sua será maior. Ou A tem maior e os dois tem a mesma massa. Ou A tem menor, mas tá com a massa muito maior do que a de B... Enfim, não tem como saber.
Resposta
a) A tem a maior capacidade calorífica.
b) Nada pode ser afirmado sobre os calores específicos.
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.67
O calor específico do cobre metálico é . Quantos de calor são necessários para aumentar a temperatura de um bloco de de cobre de para ?
Passo 1
Essa questão é aplicação de fórmula!
A fórmula de calor que utilza o calor específico é:
O famoso “que macete!”
Tá vendo que o calor específico tá em e a temperatura tá em ? Isso não vai ser um problema porque as variações em temperatura nos dois sistemas são equivalentes, ainda que as temperaturas em si mudem.
Pra não ficar nenhuma dúvida, vamos fazer dos dois jeitos.
Passo 2
Usando os dados que temos:
Passo 3
Mudando as temperaturas para Kelvin:
E aplicando a fórmula:
Resposta
Exercício Resolvido #6
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.51
Uma amostra de 2,2g de quinona ( é queimada em uma bomba calorimétrica cuja capacidade calorífica é . A temperatura do calorímetro aumenta de para . Qual é o calor de combustão por grama de quinona? E por mol de quinona?
Passo 1
O calor medido pelo aumento da temperatura do calorímetro corresponde ao calor de combustão da quinona que colocamos na bomba calorimétrica!
Ou seja,
Onde o calor de combustão ficou negativo por ser calor perdido, enquanto o do calorímetro é calor recebido.
Para calcular o , podemos usar a equação:
Passo 2
Esse que achamos no passo 1 é para queimar a quantidade de quinona que colocamos no calorímetro, ou seja, 2,2g!
Para queimar 1g:
E para queimar 1 mol (:
Resposta
Exercício Resolvido #7
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.53
Sob condições de volume constante o calor de combustão da glicose é 15,57 kJ/g. Uma amostra de 2,5g de glicose é queimada em uma bomba calorimétrica. A temperatura do calorímetro aumenta de .
a) Qual é a capacidade calorífica total do calorímetro?
b) Se o tamanho da amostra de glicose fosse duas vezes maior, qual seria a variação de temperatura do calorímetro?
Passo 1
a) Quando a gente queima alguma coisa no calorímetro, o calor recebido pelo calorímetro é igual a menos o calor liberado pela combustão (é por isso que usamos o calorímetro para medir calores de reação)...
Ou seja,
Além disso,
Onde C é a capacidade calorífica do calorímetro.
Como queimamos 2,5g de glicose, e para cada grama queimada é liberado 15,57kJ, liberamos:
Passo 2
Substituindo os dados na equação do
Passo 3
b) Se o tamanho da amostra de glicose fosse 2x maior, o seria 2x maior também!
Logo,
Agora que já sabemos a capacidade calorífica do calorímetro podemos calcular
Resposta
a)
b)
Exercício Resolvido #8
Lista de exercícios UFERSA.
Calcule o calor que deve ser fornecido a uma chaleira de cobre de massa 500 g, que contém 750 g de água, para aumentar sua temperatura de até o ponto de ebulição de água .
Dados: calor específico do cobre =
Calor específico da água =
Passo 1
Para conseguirmos fazer a água chegar ao seu ponto de ebulição, precisamos que a chaleira também chegue a
Ou seja, o calor fornecido deve ser o calor necessário para aquecer a chaleira + calor necessário para esquentar a água.
Passo 2
Substituindo os valores...
Resposta
61,25 kcal