Trabalho de Expansão
Teoria
Opaa! Bora aprender sobre o Trabalho de Expansão de um gás com o RespondeAí?!
O trabalho é a energia necessária para deslocar um corpo contra uma força, certo?!
Aqui vamos focar no Trabalho de Expansão que ocorre quando há uma variação no volume do sistema.
Como Calcular o Trabalho de Expansão de um Gás?
Vamos imaginar um gás dentro de um cilindro, com um pistão em cima dele. O trabalho realizado pelo gás para fazer o pistão subir depende da pressão externa, já que ela está relacionada à força que segura o pistão.
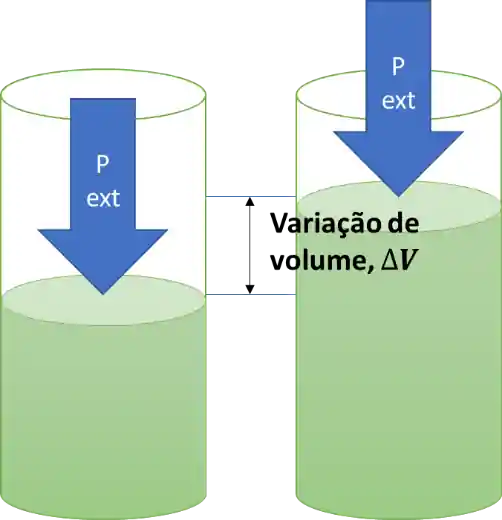
O trabalho é dado pelo produto da força pelo deslocamento:
A força por sua vez é dada pela pressão vezes a área de aplicação da força, substituindo:
A variação do volume
MAAAAS, muita atenção: quando estamos fazendo uma expansão, quem está realizando o trabalho é o gás, então temos que prestar atenção no sinal!!!
Lembrando que o trabalho feito pelo sistema é
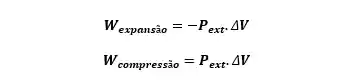
Observação: se essa expansão for feita no vácuo, onde
Processo reversível x irreversível
Na termodinâmica, um processo reversível é um processo que pode ser revertido por uma mudança infinitesimal (infinitamente pequena) de uma variável!
Calma, vamos voltar ao nosso exemplo do pistão e do gás. Se a pressão externa é igual a pressão do gás dentro do cilindro, o pistão fica parado, certo?
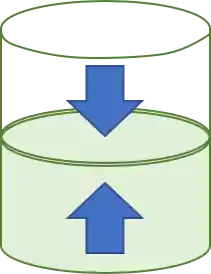
Agora, imagina que uma mudança muito muito muito pequena de pressão do lado de fora faz com que o pistão desça um pouco ou que um aumento da pressão infinitamente pequeno do lado de dentro faça com que o pistão suba um pouco.
Nesse caso, o processo vai ser reversível, já que uma mudança muito pequena do lado de fora ou de dentro do cilindro fez diferença no sistema!
Já para um processo irreversível, vamos pensar em uma situação onde a pressão externa é
Transformação isotérmica reversível de um gás
Agora que vimos a definição de processo reversível, podemos estudar a transformação isotérmica reversível de um gás!
Transformação isotérmica significa que a transformação é feita à temperatura constante!
Se a transformação for reversível, conseguimos derivar a equação do trabalho à P constante para chegar à relação:
Onde
É importante também lembrar que, como é um trabalho de expansão, o trabalho é realizado pelo sistema, e, logo, é negativo.
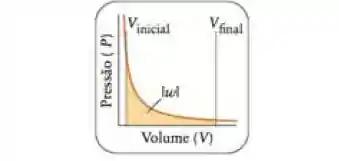
Traçando um gráfico P x V, podemos calcular o trabalho pela área embaixo da curva, ou seja, a integral dessa função:
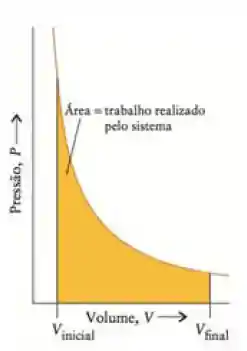
Se a pressão externa mudasse infinitesimalmente em algum momento da expansão, o pistão se moveria pra dentro, diminuindo o trabalho. Logo, o trabalho que o gás realiza durante uma expansão isotérmica reversível é o maior trabalho de expansão possível.
Resumo
Podemos realizar um trabalho de expansão à:
- Pressão constante – processo isobárico
Calculamos o trabalho por aquela fórmula que vimos antes, seja ele reversível ou irreversível.
- Volume constante – processo isovolumétrico
Como o trabalho de expansão depende do volume, se
então . - Temperatura constante – processo isotérmico
Se o processo for reversível, calculamos ele pela fórmula:
Ou, simplesmente, pela área embaixo do gráfico P x V:
Exercício:
Calcule o trabalho em cada um dos seguintes processos, começando com uma amostra de gás em um sistema com pistão com
a) expansão irreversível contra a pressão externa constante de
b) expansão reversível isotérmica até o volume final
Confira a resolução desse problema no nosso vídeo aqui em baixo 👇
Agora vamos praticar com mais exercícios?!
Processo reversível x irreversível
Resumo
Exercício:
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp281-Exercício 7.23
Calcule o trabalho em cada um dos seguintes processos, começando com uma amostra de gás em um sistema com pistão com , e :
a) expansão irreversível contra a pressão externa constante de 1 atm, até o volume final ;
b) expansão reversível isotérmica até o volume final .
Passo 1
a) Em um processo à pressão constante, calculamos o trabalho de expansão através da fórmula:
Usando os dados iniciais que temos,
Ou, se quisermos calcular direto em Joule, podemos trabalhar no SI:
Daí:
Passo 2
b) Para uma expansão reversível isotérmica, devemos usar a fórmula:
Para começar, precisamos calcular o número de mols de gás dentro do sistema!
Como temos a temperatura, a pressão e o volume, podemos usar a lei dos gases ideais para calcular o número de mols:
Agora, só precisamos aplicar na fórmula:
Resposta
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp249-Exercício 7.5
Suponha que de moléculas de um gás ideal, e , se expanda de a e atinja a pressão final de por dois caminhos diferentes.
a) O caminho A é uma expansão isotérmica reversível.
b) O caminho B tem duas partes. Na etapa 1, o gás esfria em volume constante até que a pressão atinja . Na etapa 2, ele é aquecido e se expande contra uma pressão constante igual a até que o volume atinja e .
Determine o trabalho realizado para os dois caminhos.
Passo 1
a) Pela fórmula da expansão isotérmica reversível,
Passo 2
b) Na etapa 1:
Como o volume é constante, .
Já que o trabalho se calcula como
Na etapa 2:
Como a pressão é constante,
Resposta
a)
b)
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp350-Exercício Teste 7.6A
Suponha que 2 mols de , tratado como um gás ideal, em 2 atm e 300K, são comprimidos isotérmica e reversivelmente até a metade do volume original, antes de serem usados para carbonatar a água. Calcule w.
Passo 1
Se o gás é comprimido, o trabalho será positivo, já que ele é feito sobre o gás!
Para calcular o trabalho em um processo isotérmico e reversível, devemos usar a equação:
Logo..
Resposta
Exercício Resolvido #4
Elaboração própria.
a) Calcule o trabalho associado à expansão isotérmica e reversível de 1 mol de gás ideal de 7L até 15,50L, em .
b) Calcule o trabalho associado com a expansão adiabática irreversível da amostra de gás descrita na parte (a) contra uma pressão atmosférica constante de 760 Torr.
Passo 1
a) Para o trabalho associado à expansão isotérmica e reversível, usamos a fórmula:
Passo 2
b) No caso da expansão à pressão constante, a gente usa a fórmula:
Resposta
a)
b)
Exercício Resolvido #5
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 281-Exercício 7.24
Uma amostra de gás em um cilindro de volume 3,42L, em 248K e 2,47 atm, se expande até 7,39L por dois caminhos diferentes. O caminho A é isotérmico e a expansão é reversível. O caminho B envolve duas etapas. Na primeira, o gás é resfriado em volume constante até 1,19atm. Na segunda, o gás é aquecido e se expande contra uma pressão externa constante de 1,19atm, até o volume final de 7,39L. Calcule o trabalho realizado nos dois processos.
Passo 1
Vamos por partes!
O caminho A:
Expansão isotérmica reversível, usamos a fórmula:
Para calcular o número de mols, precisamos da lei dos gases ideais:
Aplicando n na fórmula do trabalho...
Passo 2
Para calcular o trabalho do caminho B, vamos calcular o de cada etapa de uma vez e depois somar as duas!
Se o gás é resfriado em volume constante,
Assim, como
É uma expansão à pressão constante, então usamos a fórmula:
Assim, podemos calcular o trabalho total do caminho B:
Resposta
Trabalho do caminho A =
Trabalho do caminho B =
Exercício Resolvido #6
Lista de exercícios ACAFE-SC.
Um gás ideal recebe calor e fornece trabalho após uma das transformações:
a) adiabática e isobárica.
b) isométrica e isotérmica.
c) isotérmica e adiabática.
d) isobárica e isotérmica.
e) isométrica e adiabática
Passo 1
Antes de mais nada, precisamos definir todas essas transformações:
- Adiabática quer dizer que o processo acontece sem a troca de calor!
- Isobárica: o processo acontece em pressão constante.
- Isotérmica: a temperatura não muda durante todo o processo.
- Isométrica: o volume é constante
Se o gás deve receber calor e fornecer trabalho, sabemos que a transformação NÃO PODE SER:
Adiabática ou isovolumétrica!
Isso porque se ela for adiabática não há troca de calor e se ela for isovolumétrica
A única letra que não tem nem adiabática nem isovolumétrica como opção é a letra D!
Resposta
Letra D