A figura abaixo um feixe de raios luminosos paralelos produzidos por um laser incide em uma esfera maciça transparente de índice de refração .
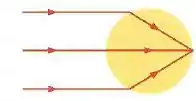
Se uma imagem pontual é produzida na superfície posterior da esfera, qual é o índice de refração da esfera?
Existe algum valor do índice de refração para o qual é produzida uma imagem pontual do centro da esfera? Se a resposta for afirmativa, qual é esse valor?
Passo 1
Se uma imagem pontual é produzida na superfície posterior da esfera, qual é o índice de refração da esfera?
Se a imagem é formada na superfície posterior da esfera, temos que . Além disso, como não sabemos exatamente onde está o laser e os raios chegam paralelos, podemos considerar . Logo:
Onde o meio 1 é o ar, com índice de refração . Logo:
Passo 2
Existe algum valor do índice de refração para o qual é produzida uma imagem pontual do centro da esfera? Se a resposta for afirmativa, qual é esse valor?
Para que a imagem esteja no centro da esfera, basta fazer :
Isso só seria possível se ou . Logo, não existe valor do índice de refração para o qual é produzida uma imagem pontual no centro da esfera.
Resposta
Não existe valor do índice de refração para o qual é produzida uma imagem pontual no centro da esfera.