Regressão Linear
Teoria
Introdução à Regressão Linear
Fala Aíí!!! Digamos que a gente tem o seguinte cenário: Temos uma variável que representa o número de gols que um time marcou em uma partida e a variável o número de tentativas que foram feitas. Observe a tabela com os dados obtidos até o final do campeonato:
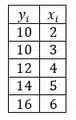
Podemos colocar os valores da tabela num gráfico que chamaremos de gráfico de dispersão. Teremos algo desse tipo:
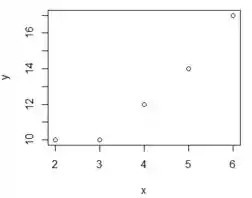
Se alguém te pedisse para encontrar a equação que melhor representa essa situação, você saberia como fazer isso?
Olhando para o gráfico, os pontos dispersos estão quase formando uma linha reta certo? Não seria exagero pensar que a equação que melhor representa essa situação será o de uma reta:
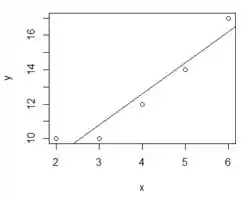
O que a gente faz em regressão linear é exatamente encontrar uma reta dessas! Beleza?!
O que a gente tem que ter na cabeça antes de ir às contas é o seguinte:
- Cada ponto dessa figura é composto de duas variáveis, que são nossos dados.
- O que a gente tá fazendo ao encontrar essa reta é tentando relacionar uma variável à outra, através de uma equação. A fórmula é a seguinte:
- Onde:
Não precisa encrencar com esse erro não! É bom representar ele nas nossas respostas finais só pra ficar matematicamente correto, mas não precisamos calcular nada sobre ele.
Beleza, mas na prática como encontramos a equação dessas retas?
Encontrando a equação da reta
Exemplo
Em uma pesquisa deseja-se encontrar a taxa de mortalidade infantil com a taxa de analfabetismo do país. Qual a reta de regressão que descreve melhor a taxa de mortalidade infantil em função do analfabetismo?
Para resolver esse problema, faz sentido estabelecermos duas variáveis:
- Taxa de Analfabetismo
- Taxa de Mortalidade Infantil
Concorda?!
Tem-se os seguintes dados:
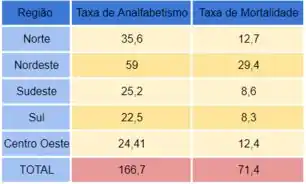
Beleza, mas antes de começar precisamos responder uma pergunta que nos ajudará a encontrar a reta: qual é nossa variável dependente e qual nossa variável independente?
Lembra que a fórmula da reta seria algo desse tipo:
Note que o valor de Y está dependendo do valor de X! Por isso chamamos Y de variável dependente e x de variável independente. Show de bola?!
No nosso caso queremos relacionar a taxa de mortalidade com a taxa de analfabetismo, ou seja, como a taxa de analfabetismo interfere na taxa de mortalidade.
Podemos dizer então que a taxa de mortalidade será nossa variável dependente (porque vai sofrer alterações com os números de analfabetos) e a taxa de analfabetismo será nossa variável independente.
Podemos montar outra tabela agora dessa forma:
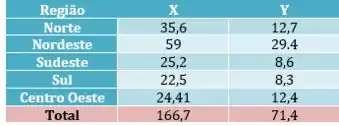
Agora vamos encontrar os coeficientes da equação da reta seguindo o passo a passo!
Lembrando que a equação deve ter uma carinha como essa:
Passo 1)
Para montarmos a função temos que descobrir o valor dos parâmetros e .
Infelizmente teremos mais fórmulas:
Masôqueee? Relaxa! Vamos ver direitinho o que cada termo aí dentro significa.
O é o número de elementos da nossa amostra. Como nosso quadro nos dá informações sobre regiões do país, . Os e são os dados individuais de cada variável. E e são as médias amostrais desses dados.
Vamos começar com o :
Vamos calcular todos esses valores com a ajuda da tabela.
Precisamos multiplicar os valores de x e y em cada linha da tabela e depois somar tudo!
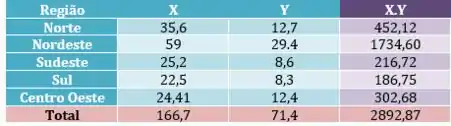
Beleza? Vamos para o próximo!
Já temos esses valores na tabela!
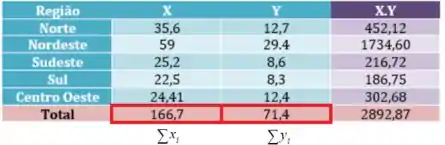
Tudo bem até aqui?
Também podemos montar uma coluna da nossa tabela calculando o valor de e depois somar os valores que encontramos:
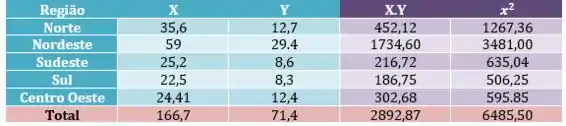
Falta só o últimos termo:
Reparem que é diferente do que calculamos anteriormente! Nesse caso vamos pegar o valor de e elevar ao quadrado. Já encontramos esse valor então:
Pronto! Temos tudo que precisamos para encontrar o coeficiente :
Passo 2)
Para o cálculo do , precisamos das médias amostrais, que vão ser dadas por:
Então:
Passo 3)
Agora podemos juntar tudo na fórmula da reta:
Essa aí é nossa melhor reta aproximada!
Encontrando a equação da reta
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Foram observados 4 lotes aleatórios de sucos concentrados, cada um com a sua respectiva quantidade (em mg) por pacote e a quantidade de água necessária (em ml).
Estime os parâmetros da reta de regressão . Onde é a quantidade em mg.
Passo 1
Bom, pra fazer isso a gente só vai precisar aplicar fórmulas.
Sendo que...
Lembrando que temos essas duas formas de escrever a variância, uma simplificada e outra não. Você pode escolher qual usar, elas dão o mesmo resultado, afinal, são a mesma coisa!
Fazendo as contas vamos ter:
Lembrando que o é a quantidade em mg e que sua média vale 300.
Com isso...
Passo 2
Pra calcular o ...
Substituindo os valores na fórmula..
Resposta
Exercício Resolvido #2
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 286.
Em seu livro Uncertainties analysis, loads and safety in Structural Engineering (Prentice Hall, 1982) – em português, Análise de incertezas, cargas e segurança em Engenharia de Estruturas -, Gary C. Hart apresenta o conjunto de dados a seguir, que nos permite investigar a relação de dependência entre duas propriedades mecânicas do concreto: módulo secante (em psi) e força de compressão (em psi).
- Obtenha um diagrama de dispersão relativo a esses dados;
- Calcule o coeficiente de correlação entre e ;
- Ajuste os dados a reta de regressão .
Passo 1
(a)
Diagrama de dispersão é colocar os pontos num gráfico;
Passo 2
(b)
Coeficiente de correlação é a fórmula:
Então vamos calcular cada parte separadamente.
Passo 3
Passo 4
Agora .
Passo 5
Agora sim:
Relaxe, dependendo dos seus arredondamento seu resultado pode ter dado um pouco diferente.
Passo 6
(c)
Vamos ajustar a reta, pra isso temos que calcular os coeficientes e :
Nossa reta de regressão seria então:
Resposta
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 2
A tabela abaixo indica o valor y do aluguel e a idade x de cinco casas.
a) Encontre a reta de MQ, supondo a relação .
b) Faça o gráfico dos pontos e da reta ajustada. Você acha que o modelo adotado é razoável?
c) Qual o significado do coeficiente angular nesse caso?
d) E do coeficiente linear?
Passo 1
Esse é um exercício clássico de regressão linear, em que são você tem os dados da amostra e precisa achar a reta de mínimos quadrados, ou seja precisa estimar α e o β, por aquelas fórmulinhas da teoria
Onde nesse caso n = 5, x = {10, 13, 5, 7, 20} e y = {4, 3, 6, 5, 2}. E lembrando que a variável com a barra em cima significa a média amostral dela.
Passo 2
Aqui é a parte chata em que você faz um monte de contas, sugiro que pegue uma calculadora
Pronto ai está a sua reta ajustada pelos MQ
Passo 3
Para fazer o gráfico de pontos basta você delimitar um espaço, marcar os pares de pontos e depois traçar a reta que foi achada no passo 2, ela deve ter mais ou menos essa cara.
Não fique triste senão ficar igual, eu (roubei) fiz no computador.
Ah, e se é razoável?! Bom, olhando para o gráfico podemos verificar que os pontos estão próximos à reta, logo, parece ser razoável.
Passo 4
Já na letra (c) ele pede pra explicar o significado do coeficiente angular, que é o α.
Como ele é o termo que está próximo de x, e x é a idade das casas, α significa que o valor médio do aluguel diminui em 0,26 vezes a cada ano que passa.
Passo 5
A letra (d) é bem parecida com a letra (c), só que precisamos explicar o coeficiente linear, β.
É o termo que está “sozinho”, e como ele é igual a y quando x=0, ele diz que o valor médio do aluguel das casas, no tempo 0 é de 6,87.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 3
Um laboratório está interessado em medir o efeito da temperatura sobre a potência de um antibiótico. Dez amostras de 50 gramas cada foram guardadas a diferentes temperaturas, e após 15 dias mediu-se a potência. Os resultados estão no quadro abaixo.
a) Faça a representação gráfica dos dados.
b) Ajuste a reta de MQ, da potência como função da temperatura.
c) O que você acha desse modelo?
d) A que temperatura a potência média seria nula?
Passo 1
Sabemos que y = {38, 43, 32, 26, 33, 19, 27, 23, 14, 21} e x = {30, 30, 50, 50, 50, 70, 70, 70, 90, 90}, basta marcar os pares de pontos no gráfico e traçar uma reta que fique razoavelmente bem distribuída entre os pontos. Exemplo:
Passo 2
Para resolvermos a letra (b), basta lembrar das fórmulas que a gente viu na teoria:
Achando todos os valores necessários, (recomendo que use uma calculadora ou até um programa de computador) teremos
Passo 3
A pergunta da (c) é, o modelo parece adequado?? Sim, com os dados que temos o modelo parece seguir uma linearidade em que y depende de x. (os valores observados não estão muito longe da reta)
Passo 4
Para respondermos a (d) basta acharmos o valor de x (temperatura), o (potência média) será 0.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 18
Os dados abaixo referem-se a meses de experiência de dez digitadores e o número de erros cometidos na digitação de determinado texto.
Dados:
a) Represente graficamente esse conjunto de dados.
b) Assumindo que um modelo de regressão linear é adequado, determine os coeficientes da equação pelo método dos mínimos quadrados.
c) Represente a reta de regressão no gráfico feito anteriormente
d) Qual a posição do ponto , em relação à reta de regressão?
e) Qual o número esperado de erros para um digitador com 5 meses de experiência?
Passo 1
Neste exercício temos uma amostra com n=10, e não confie nesses dados que ele dá no problema, eles estão errados, tirando o somatório de y refaça todos.
Passo 2
Para montarmos o gráfico basta pegarmos os pares (xi , yi) e ordenar no gráfico, assim:
Passo 3
Para resolvermos a letra c, isto é, acharmos a reta da regressão, precisamos achar os valores de α e β, basta lembrarmos das fórmulas nos valores que calculamos na calculadora, (de novo não confia no exercício, ele fura fila no bandejão).
Aplicando os dados:
Logo a sua reta terá a cara:
Passo 4
Agora para traçar a reta pegue uns dois pontos de y na equação encontrada acima e veja que x é seu par, e trace uma reta, ficará mais ou menos assim
Passo 5
Para a nossa sorte já calculamos as médias amostrais, quando achamos β, logo é só achar onde fica o par (5,5,17). Uma dica o par das médias amostrais de x e y vai sempre estar sobre a reta, para provar basta aplicar o x na equação da reta e verá que o resultado será y.
Passo 6
Para resolver a letra (e), é basicamente repetir o passo que fizemos na d, mas trocando o x=5,5 para x=5.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 18
Sejam Y = despesa com viagem, X = duração da viagem (em dias). Para uma amostra com n = 102 obteve-se
a) Obter a reta
b) Qual o significado prático de ?
Passo 1
Neste exercício temos uma amostra com n=102, e não se assuste que dessa vez não tem tabela, você tem todos os dados que precisa na questão e até uns que nem precisa. Preste atenção também que nesse caso alfa e beta estão trocados.
Passo 2
Para resolvermos a letra a, isto é, acharmos a reta da regressão, precisamos achar os valores de α e β, aplicando nas fórmulas que já foram vistas antes
Aplicando os dados:
Logo a sua reta terá a cara:
Passo 3
Para entender o significa prático das constantes vamos reler o problema e perceber que, o diz que com zero dias de viagem, ou melhor, o custo inicial da viagem é de 10. Já o diz que a cada dia que a passa a viagem fica 12x mais cara.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 2
Um administrador de uma grande sorveteria anotou por um longo período de tempo a temperatura média diária, em ºC (X), e o volume de vendas diária de sorvete, em kg (Y). Com os dados, estabeleceu uma equação de regressão, resultando em:
a) Qual o consumo esperado de sorvete num dia de 27ºC?
b) Qual o incremento esperado nas vendas de sorvete a cada 1ºC de aumento da temperatura?
Passo 1
Esse é um exercício ótimo para entender o significado das constantes, você já tem a reta montada pelo enunciado, daí jogar o valor das constantes no lugar certo.
Passo 2
Na letra A, você apenas precisa sacar que o como a temperatura média diária (x) é 27ºC, logo apenas precisamos substituir o x na reta por 27.
Então o consumo esperado de sorverte em um dia é de 49,1kg
Passo 3
A letra B, é similar a letra A, a única diferença é que você não vai exatamente substituir na reta, e sim entender o sentido. Pois é possível perceber que a cada vez que x aumenta em 1ºC, a equação é acrescida de 1,8kg, que é o valor da constante ligada a x.
Então o incremento esperado é uma adição de 1,8kg.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 2
Para cada uma das situaçãos abaixo, grafe os valores em um diagrama e se uma equação linear parecer apropriada para explicar os dados, determine os seus parâmetros
(i)
(ii)
Passo 1
O que o exercício está pedindo é, para cada amostra, montar um gráfico com os pares (x,y) e olhar para esse gráfico e ver se ele tem “cara” de linear, caso tenha montar a equação por mínimos quadrados pelas fórmulinhas que a gente viu na teoria. Vamos lá!!
Passo 2
Pegamos o primeiro conjunto de dados, e colocamos em um gráfico:
Agora olha para essa distribuição de pontos. Parece uma reta?? Não né, então nem precisa montar a reta. uhul!! Aí que você fica triste por não poder aplicar seu vasto conhecimento, mas fé que no próximo vai parecer uma reta.
Passo 3
Agora pegamos o segundo conjunto de dados, e botamos no gráfico.
Parece uma reta?? Parece!!! (se você disse que não ta com a mente muito fechada, se esforça!!). Vamos calcular as constantes agora.
Passo 4
Para acharmos os valores é naquele esquema, formuletas que vimos na teoria
Agora temos que fazer toda essas somas, muita atenção!! É muito fácil errar aqui, use uma calculadora
Então a reta que queremos é:
Resposta
Ei, a resposta está no passo a passo :)