Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Série de Taylor

Ver Todos os Exercícios

Teoria

Fala aí, hoje nós vamos bater um papo sobre a série de Taylor.

O que é a Série de Taylor?

A série de Taylor é uma série de funções que é utilizada para reescrevermos uma função como um polinômio! Ela tem essa carinha aqui:

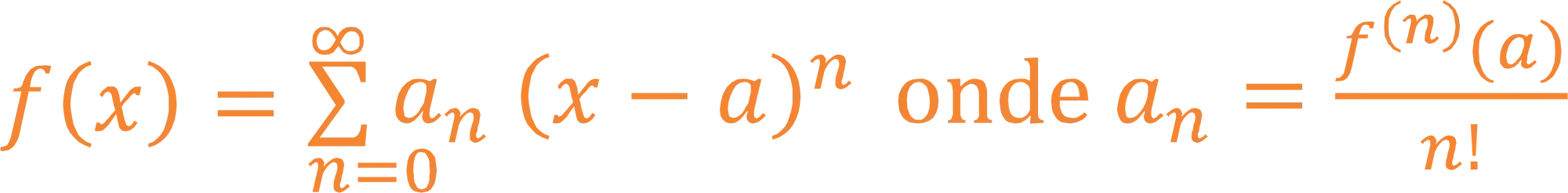
Série de Taylor
Série de Taylor

Eu sei…assusta! Mas não precisa se apegar agora, a gente vai aprender com calma a trabalhar com ela jájá! Por enquanto você só precisa saber que nos exercícios, a gente vai pegar uma função e reescrever ela no formatinho da série de Taylor! Isso é, como polinômio!

Lembrando que polinômios são expressões dessa maneira aqui:

Onde:

  • , , , ..., , , são constantes, e;
  • é a variável

Note que em um polinômio nós temos vários termos e cada um desses termos tem a variável elevada a expoentes, desde o expoente , até o expoente .

Quando falamos que vamos reescrever uma função em série de Taylor, o que vamos fazer é pegar essa função e escrever ela como um polinômio. O interessante é que a série de Taylor é uma série infinita, ou seja, existem infinitos termos, então vamos reescrever a função como um polinômio com infinitos termos, ou seja, o expoente tende ao infinito.

Sempre que a gente tiver uma função infinitamente derivável e definida em um intervalo da série, poderemos escrever essa função com essa cara aqui:

Onde:

  • é um valor de que escolhemos para ser o ponto central da nossa série, e;
  • é a derivada de ordem no ponto

Para reescrevermos a função em série de Taylor temos que percorrer o valor de de até , e cada valor de nos dará um termo do nosso polinômio.

Calma. Eu sei que pode estar confuso, então vem comigo fazer um exemplo prático. Vai ficar mais fácil de entender, pode confiar!

📢 Clique para ver mais:

Como Calcular a Série de Taylor?

Vamos reescrever a função em série de Taylor e vamos escolher o valor para ser o ponto central da nossa série.

PASSO 1: Achar pelo menos até a quarta derivada da função

PASSO 2: Substituir o ponto nas derivadas encontradas

A partir desse ponto nós conseguimos achar os primeiros termos da série.

Substituindo os valores que encontramos, temos:

Mas falamos lá em cima que a série de taylor é infinita, então temos mais infinitos termos para acrescentar aí. Teremos que ficar fazendo as derivadas infinitamente e montando esses termos? NÃO. O que vamos fazer é encontrar um padrão para os termos em função de e escrevermos como um somatório, daquele jeitinho que mostramos lá no início. Então bora continuar o nosso passo a passo.

PASSO 3: Encontrar um padrão para as derivadas

Repara que para derivadas de ordem par, o resultado deu zero ( e ). Já as derivadas de ordem ímpar, o resultado variou entre e . Então vamos dividir nossa análise em duas para entender melhor esse padrão:

  • Análise 1: Todo mundo que tem par vai ser zero. Então galerinha, podemos chamar o nosso expoente de (onde é , , , ...), pois assim sempre teremos um número par. No ponto 0 ficará:

  • Análise 2: Agora se temos um expoente impar, a derivada intercala entre e . Então para ter um impar, eu posso dizer que (onde é , , , ...). Agora precisamos achar um padrão de quando ele será e quando será .

Quando , o resultado da derivada é positivo e o vale:

Quando , o resultado da derivada é negativa e o vale:

Note que encontramos um padrão: Quando for par, o resultado da derivada positivo e quando for ímpar, o resultado da derivada é negativo:

PASSO 4: Aplicar o padrão encontrado no PASSO 3.

Como dividimos esse exemplo em duas partes, temos que dividir a série também em duas partes, uma para quando temos expoentes pares e outra para quando temos expoentes ímpares:

Vimos que , então o primeiro somatório todo anula. Além disso, vimos que , então, temos:

E prontinho, achamos a série de Taylor para a função .

Lembra sempre de seguir o passo a passo:

  1. Encontrar as derivadas, no mínimo até a quarta derivada;
  2. Aplicar as derivadas no ponto central da série;
  3. Encontrar um padrão para as derivadas;
  4. Aplicar o padrão encontrado na fórmula da série de Taylor

Nós temos esse conteúdo em vídeo também. Se você preferir é só conferir aqui! 👇

Série de Maclaurin

A Série de Maclaurin é um caso especial da série de Taylor, quando a=0, ou seja quando a série está centrada na origem.

Série centrada na origem
Série centrada na origem

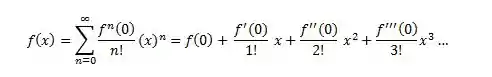
As principais séries de Maclaurin:

Principais séries de Maclaurin
Principais séries de Maclaurin

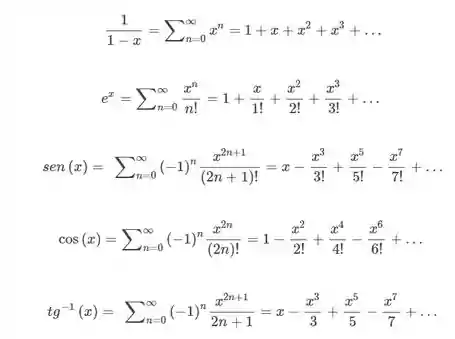
Exercício: Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada.

Passo 1: Conferir a tabela da série de Maclaurin

A questão pede pra gente olhar a tabela, né não? Bom então vamos olhar né, mandou a gente obedece:

tabela da série de Maclaurin
tabela da série de Maclaurin

O que a gente tem que fazer é olhar nessa tabela no lado esquerdo (o lado sem somatório) e ver se existe alguma lei de formação parecida com a do nosso enunciado:

Bem, olhando pra tabela da pra ver que podemos excluir todas as funções trigonométricas e aquele O que talvez mais se pareça seria a série binomial:

Nos próximos passos o que vamos fazer é mexer o suficiente nessa equação pra que o lado esquerdo fique igualzinho a nossa .

Passo 2: Reescrever a função f(x)

Vamos reescrever a função como:

Passo 3: Manipular a série binominal

Pra começar vamos olhar  e e a série binomial uma do lado da outra:

Ambas tem um polinômio de primeiro grau de elevado a uma constante. Se a primeira esta elevada a e a segunda tá elevada a , temos que , logo:

O interior desse polinômio não é exatamente e sim ! Portanto podemos fazer:

Manipulando essa equação, ficamos com:

Como o lado esquerdo ficou exatamente idêntico a nossa f(x), fechamos nossa questão:

Prontinho! Agora vamos praticar com mais exercícios?!

Como Calcular a Série de Taylor?

Série de Maclaurin

Exercício: Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada.

Exercícios Resolvidos

Exercício Resolvido #1

PUC-RJ - Cálculo 3 - P3 2013.2 - 4

Ache a expansão em série de potências f x = e x + e - x 2 em torno de x = 0 .

Passo 1

Repara que temos um termo e x e outro e - x , no numerador, então vamos relembrar da teoria a representação da serie de Taylor cada um.

Para uma dada função g x = e x , podemos representar assim:

g x = ∑ n = 0 ∞ x n n !

E analogamente, a série de Taylor para uma dada função h x = e - x temos:

h x = ∑ n = 0 ∞ - 1 n x n n !

Passo 2

Verificar os raios de convergência das séries. Para isso, vamos aplicar o Teste da Razão, que nos diz que a série converge quando,

lim n → ∞ ⁡ c n + 1 c n < 1

Para g ( x ) , teremos

lim n → ∞ ⁡ x n + 1 n + 1 ! × n ! x n = lim n → ∞ ⁡ x n + 1 = 0

Para h ( x ) , teremos,

lim n → ∞ ⁡ - 1 n + 1 x n + 1 n + 1 ! × n ! - 1 n x n = lim n → ∞ ⁡ - x n + 1 = 0

Como raio de convergência é dado por R = 1 / L , onde L é o resultado do limite calculado. Temos que os raios de convergência valem infinito. Isso é importante para podermos escrever a função f x da seguinte maneira, em termos de g x e h x :

f x = g x + h x 2

Passo 3

Reescrevendo a função, teremos:

f x = 1 2 ∑ n = 0 ∞ 1 n ! x n + - 1 n x n

Repare que a expansão só terá termos com n par! Pois se n for ímpar, o termo é nulo, visto que haverá um termo x n - x n = 0 . Por exemplo, para n = 3

f x = 1 2 ∑ n = 0 ∞ 1 3 ! x 3 + - 1 3 x 3 = 1 2 ∑ n = 0 ∞ 1 3 ! x 3 + ( - x 3 )

Portanto como só teremos números pares, podemos chamar n = 2 k (pois todo número multiplicado por 2 é par) e a expansão será:

f x = 1 2 ∑ n = 0 ∞ 1 2 k ! x 2 k + - 1 2 k x 2 k

=   1 2 ∑ n = 0 ∞ 1 2 k ! x 2 k + x 2 k

= 1 2 ∑ k = 0 ∞ 1 2 k ! 2 x 2 k = ∑ k = 0 ∞ x 2 k 2 k !

Resposta

∑ k = 0 ∞ x 2 k 2 k !

Exercício Resolvido #2

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 709, exercício 7 (adaptado)

Encontre a Série de Taylor de f ( x ) em torno do ponto a = 0 . [Suponha que f tenha expansão em uma série de potências. Não mostre que R n ( x ) → 0 .] Também encontre o raio de convergência associado.

f x = cos ⁡ x

Passo 1

Vamos calcular as derivadas de f ( x ) e procurar um padrão.

f ' x = - sen ⁡ x

f ' ' x = - cos ⁡ x

f ' ' ' x = sen ⁡ x

f ' ' ' ' x = cos ⁡ x  

Logo, podemos escrever o seguinte:

f 2 n = - 1 n cos ⁡ x

f 2 n + 1 = - 1 n + 1 sen ⁡ x

Temos, portanto, expressões diferentes para índices pares e ímpares.

Passo 2

Vamos, agora, montar a Série de Taylor.

Para a série em torno de zero, temos:

cos ⁡ x = ∑ n = 0 ∞ f n 0 x n n !

Precisamos substituir as expressões que encontramos para a derivada. Repare:

f 2 n 0 = - 1 n cos ⁡ 0 = - 1 n

f 2 n + 1 0 = - 1 n + 1 sen ⁡ 0 = 0

Assim, restam apenas os índices pares. Reescrevendo a série para os índices ( 2 n ) , temos:

cos ⁡ x = ∑ n = 0 ∞ f 2 n 0 x 2 n ( 2 n ) !

Substituindo a expressão da derivada:

cos ⁡ x = ∑ n = 0 ∞ - 1 n x 2 n ( 2 n ) !

Passo 3

Vamos, então, calcular o raio de convergência, pelo Teste da razão. Na forma simplificada para séries de potências temos:

c n = - 1 n ( 2 n ) !

Então

lim n → ∞ ⁡ c n + 1 c n = lim n → ∞ ⁡ - 1 n + 1 ( 2 n + 1 ) ! × 2 n ! - 1 n = lim n → ∞ ⁡ - 1 n + 1 ( 2 n + 2 ) ! × 2 n ! - 1 n

= lim n → ∞ ⁡ - 1 2 n + 2 ( 2 n + 1 ) = 0 = L

Como R = 1 / L , tomando a convenção que 1 / 0 = ∞ , temos R = ∞ .

Resposta

cos ⁡ x = ∑ n = 0 ∞ - 1 n x 2 n 2 n !

R = ∞

Exercício Resolvido #3

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 709, exercício 19

Encontre a Série de Taylor de f ( x ) centrada no valor dado de a . [Suponha que f tenha expansão em uma série de potências. Não mostre que R n ( x ) → 0 .]

f x = 1 / x

a = 9

Passo 1

Para achar a representação em série de Taylor de uma função, a gente sempre começa buscando um padrão nas derivadas.

Vamos calcular as derivadas de f ( x ) e procurar um padrão.

f ' x = - x - 3 / 2 2

f ' ' x = 1 ⋅ 3 ⋅ x - 5 / 2 2 ⋅ 2

f ' ' ' x = - 1 ⋅ 3 ⋅ 5 ⋅ x - 7 / 2 2 ⋅ 2 ⋅ 2

Repare que, a cada derivação, aparece mais um 2 multiplicando o denominador, de modo que temos 2 n .

Ao mesmo tempo, o expoente de x perde uma unidade a cada n (começando em - 1 / 2 , na função primitiva).

No numerador, nós temos a multiplicação de números ímpares, desde 1 até ( 2 n - 1 ) .

O sinal se alterna, ou seja, temos um termo - 1 n (sempre verifique se esse índice está certo testando valores de n ).

Logo, podemos escrever o seguinte:

f n x = - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … 2 n - 1 2 n x - 1 2 - n

Passo 2

Vamos, agora, montar a Série de Taylor! Lembra que ela tem essa cara aqui,

∑ n = 0 ∞ f n a ( x - a ) n n !

Para a série em torno de a = 9 :

1 x = ∑ n = 0 ∞ f n 9 ( x - 9 ) n n !

Precisamos, agora, substituir a expressão que encontramos para a derivada.

f n 9 = - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … 2 n - 1 2 n ( 9 ) - 1 2 - n =

= - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … 2 n - 1 2 n ⋅ 9 1 + 2 n 2 =

= - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … ( 2 n - 1 ) 2 n ⋅ 3 2 ( 1 + 2 n ) 2 =

= - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … ( 2 n - 1 ) 2 n ⋅ 3 1 + 2 n

Portanto, temos a seguinte série

1 x = ∑ n = 0 ∞ - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … 2 n - 1 ( x - 9 ) n 2 n ⋅ 3 1 + 2 n ⋅ n !

Resposta

1 x = ∑ n = 0 ∞ - 1 n 1 ⋅ 3 ⋅ 5 ⋅ 7 … 2 n - 1 ( x - 9 ) n 2 n ⋅ 3 1 + 2 n ⋅ n !

Exercício Resolvido #4

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 709, exercício 6 (adaptado)

Encontre a Série de Taylor de f ( x ) em torno do ponto a = 0 . [Suponha que f tenha expansão em uma série de potências. Não mostre que R n ( x ) → 0 .] Também encontre o raio de convergência associado.

f x = ln ⁡ ( 1 + x )

Passo 1

Já resolvemos essa questão em um exemplo, comparando sua derivada com a soma da Série geométrica. Vamos, agora, resolver encontrando a Série de Taylor.

Vamos calcular as derivadas de f ( x ) e procurar um padrão.

f ' x = 1 x + 1

f ' ' x = - 1 x + 1 2

f ' ' ' x = 2 x + 1 3

f ' ' ' ' x = - 6 x + 1 4

Temos os coeficientes: 1 ,   1 ,   2 ,   6 . Veja que

e m   n = 1 → 1 = 0 !

e m   n = 2 → 1 = 1 !

e m   n = 3 → 2 = 2 !

e m   n = 4 → 6 = 3 !

Temos, então, sempre n - 1 ! .

Agora, vamos analisar os sinais. Já vimos que eles se alternam, então, temos ( - 1 ) elevado a alguma potência, mas qual? Veja que nos n ’s pares, temos sinal negativo para o f n , enquanto nos ímpares, temos positivos.

Se escrevermos - 1 n , essa regra não é obedecida, mas escrevendo - 1 n - 1 , os sinais ficam corretos.

e m   n = 1 → - 1 1 - 1 = 1

e m   n = 2 → - 1 2 - 1 = - 1

E assim por diante!

Logo, podemos escrever o seguinte:

f n x = n - 1 ! - 1 n - 1 ( x + 1 ) n

Passo 2

Montar a Série de Taylor.

Para a série em torno de zero, temos, então:

ln ⁡ ( 1 + x ) = ∑ n = 0 ∞ f n 0 x n n ! = f 0 + f ' ( 0 ) 1 ! x + f ' ' ( 0 ) 2 ! x 2 …

Na verdade, como f 0 = ln ⁡ ( 1 + 0 ) = 0 , podemos escrever que a série começa em n = 1 :

ln ⁡ ( 1 + x ) = ∑ n = 1 ∞ f n 0 x n n !

Precisamos, agora, substituir a expressão que encontramos para a derivada.

f n 0 = n - 1 ! - 1 n - 1 ( 0 + 1 ) n = n - 1 ! - 1 n - 1

Portanto, temos a seguinte série

ln ⁡ ( 1 + x ) = ∑ n = 1 ∞ n - 1 ! - 1 n - 1 x n n ! = ∑ n = 1 ∞ - 1 n - 1 x n n

Foi importante tiramos o n = 0 do somatório, porque isso causaria uma indeterminação (teríamos 0 no denominador).

Observação: No exemplo que vimos na teoria, tínhamos encontrado o seguinte somatório:

ln ⁡ ( 1 + x ) = ∑ k = 0 ∞ - 1 k x k + 1 k + 1

Se você reparar, é a mesma série, basta fazermos n = k + 1 .

Passo 3

Vamos, então, calcular o raio de convergência, pelo Teste da razão. Na forma simplificada para séries de potências temos:

c n = - 1 n - 1 n

Então

lim n → ∞ ⁡ c n + 1 c n = lim n → ∞ ⁡ - 1 n n + 1 × n - 1 n - 1 =

lim n → ∞ ⁡ - n n + 1 =

lim n → ∞ ⁡ - n n ( 1 + 1 / n ) = 1 = L

Como R = 1 / L , temos R = 1 .

Resposta

ln ⁡ ( 1 + x ) = ∑ n = 1 ∞ - 1 n - 1 x n n

R = 1

Exercício Resolvido #5

UFRJ - Cálculo 4 - P1 2014.2 - 1b

Seja

f x = ∑ n = 1 + ∞ n + 1 2 n 3 x - 2 n

Determine f 17 ( 2 ) , onde f ( 17 ) é a décima sétima derivada de f ( x ) .

Passo 1

Pelo Teorema de Taylor, temos que

f x = ∑ n = 0 + ∞ f n ( 2 ) x - 2 n n !

Passo 2

Comparando as duas séries, nós temos que:

c n = f n ( 2 ) n ! = n + 1 2 n 3

Fazendo n = 17 , isso nos dá:

f 17 ( 2 ) 17 ! = 17 + 1 2 17 3

Multiplicando os dois lados por 17:

f 17 ( 2 ) 16 ! = 18 17 2

f 17 2 = 18 17 2 16 !

Resposta

f 17 2 = 18 17 2 16 !

Exercício Resolvido #6

UFRJ - Cálculo 4 - P1 2015.1 - 2b

Considere a série de potências

f x = ∑ n = 1 + ∞ x + 1 n - 1 2 n n 3

Encontre f 15 ( - 1 ) (a derivada de ordem 15 da função f em x = - 1 ).

Passo 1

Pelo Teorema de Taylor, temos que

f x = ∑ n = 0 + ∞ f n ( - 1 ) x + 1 n n !

Bom, como a série do problema tem x + 1 n - 1 , vamos dar uma ajeitada para podermos comparar com o formato de Taylor:

f x = ∑ n = 1 + ∞ x + 1 n - 1 2 n n 3 = ∑ n = 0 + ∞ x + 1 n 2 n + 1 ( n + 1 ) 3

Passo 2

Agora, vamos comparar as duas séries:

f x = ∑ n = 0 + ∞ x + 1 n 2 n + 1 ( n + 1 ) 3 = ∑ n = 0 + ∞ f n ( - 1 ) x + 1 n n !

Isso nos dá

1 2 n + 1 ( n + 1 ) 3 = f n ( - 1 ) n !

Para n = 15 :

1 2 16 ( 16 ) 3 = f 15 ( - 1 ) 15 !

O que nos dá

f 15 - 1 = 15 ! 2 16 ( 16 ) 3

Resposta

f 15 - 1 = 15 ! 2 16 ( 16 ) 3

Exercícios de Livros Relacionados

Demonstre que a série obtida no Exercício 11 representa x para todo x .
Encontre a série de Taylor de f centrada em 4 se f n 4 = - 1 n n ! 3 n n + 1 Qual é o raio de convergência da série de Taylor?
Encontre a série de Maclaurin f ( x ) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n → 0 .] Também encontre o raio de converg
Use a série binomial para expandir a função como uma série de potência. Diga o raio de convergência. 1 1 + x 4
Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada. f x = sen ⁡ π x