Calcule a integral definida
Passo 1
Você pode estar pensando: meu Deus! Eu nunca vi tanto assim em uma integral...
Primeiro de tudo, essa é uma integral definida, por conta desses numerozinhos em cima e em baixo da integral.
Eles são chamados de limites de integração. Quando uma integral tem esses limites de integração, ela é chamada de integral definida!
![]()
Mas essa integral provavelmente assusta por causa do dentro da raiz quadrada, estou certo? Talvez fosse mais fácil se dentro da raiz quadrada tivesse algo mais simples.
Então, se o que atrapalha a gente é esse , porque não tentamos nos livrar dele? E podemos fazer isso, criando uma nova variável que deve ficar no lugar de .
Essa técnica de criar uma nova variável para substituir um termo difícil da integral é chamada de substituição simples! Ela é uma das técnicas de integração mais importantes!
A intenção é transformar nossa integral difícil que está escrita em função de , em uma nova integral mais simples escrita agora em função de .
Se a gente substituir por esse , a integral vai ficar:
A cara dela já está melhorzinha, né? Mas ainda não resolvemos nosso problema! Nós precisamos trocar tudo que está escrito em , por relações equivalentes em !
No próximo passo a gente vai descobrir como substituir e por alguma relação em e .
Passo 2
Vamos atrás do . E para descobrir quanto vale , a gente precisa derivar o em relação a !
Como vamos derivar uma soma, podemos derivar cada pedaço separadamente:
Derivamos usando a regra do peteleco! Nessa regra, o expoente cai na frente de multiplicando e ao cair ele perde uma unidade no expoente, deixando pra trás um expoente .
Agora é a vez do 9. Temos que nos lembrar que a derivada de uma constante vale zero. Logo, a derivada de vale zero!
Resumindo, a derivada de vale:
Show, olha o que a gente estava procurando ali embaixo do . Se a gente passar o para o lado direito teremos:
Pra deixar o sozinho, vamos passar agora o para o lado esquerdo da equação:
Agora a gente pode substituir o também o da integral pelo .
Aqui temos dois detalhes importantes. Não podemos usar os limites de integração, porque eles eram da variável e não da variável . Então faremos a integração em , sem os limites mesmo e quando a gente voltar pra , aí sim colocamos os limites.
Além disso, na nossa integral temos multiplicando e dividindo, então podemos cancelar um com o outro, sobrando só:
Agora temos uma integral toda em e bem mais simples de se resolver. Partiu resolvê-la, então.
Passo 3
Dividir por é a mesma coisa que multiplicar por . Por isso, podemos transformar o que está dividindo o em .
Primeiro, temos que lembrar que a constante pode ser tirada da integral!
Depois, precisamos lembrar que calcular a raiz quadrada de um número é a mesma coisa que elevar o número a . Ou seja, é igual a .
Agora está claro que precisamos integrar uma potência de .
Pra nossa sorte, existe uma regrinha bem simples que vai ajudar a encontrar rapidinho a integral de qualquer potência de . A regrinha é: soma no expoente e divide por esse resultado. Ou seja, a regrinha geral, ficaria assim:
Para usar essa regra, vemos que o expoente de vale . E vai ficar assim:
Vamos resolver esse , colocando os dois valores em forma de fração com o mesmo denominador. Ou seja, vamos escrever o 1 como sendo
Agora a gente soma em cima e repete em baixo:
Aplicando essa regra, achamos:
Para tirar o que está no denominador da fração a gente coloca ele invertido na frente multiplicando o
Simplificando o :
Já estamos quase lá. Agora vamos usar a regrinha do expoente fracionário, onde a gente pode transformar ele em raiz, assim ó:

Beleza, conseguimos integrar, mas lembra que nossa integral era em e tinha os limites de integração?
Passo 4
Pra voltarmos pra variável certa, vamos lembrar que chamamos o . Então vamos substituir nosso e colocar os limites de integração de .
Passo 5
Finalmente vamos usar os limites de integração!
Fazemos isso, substituindo o pelos dois limites, um de cada vez na função. Primeiro, nós vamos trocar o pelo limite de cima (pelo ) e depois vamos trocar pelo limite debaixo (pelo ). E então subtraímos as expressões encontradas:
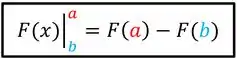
Usando essa regra, a expressão vira:
Agora vamos resolver essas contas aí com cuidado. Primeiro os parênteses que estão dentro das raízes:
Agora em e , podemos jogar o pra fora da raiz. Então primeiro a gente tira a raiz quadrada e depois eleva a 3. Isso facilita as nossas contas já que o e o tem raízes quadradas.
Então:
Agora a gente faz a subtração das frações:
Já estão com o mesmo denominador, então a gente só resolve em cima e repete em baixo:
Pronto! Finalmente achamos o resultado da integral! Mas vamos recordar esse passo a passo da substituição por partes:
- A gente criou uma nova variável .
- Depois, a gente substituiu o da integral por algo relacionado a e o da integral por algo relacionado a .
- Além disso, a gente precisou tirar limites de integração. Eles serviam para a integral de , mas não para a integral de .
- Integramos a função encontrada em .
- Voltamos para a variável .
- Por fim, substituímos os limites de integração!
- Fizemos umas continhas e FIM!