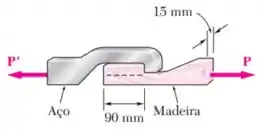
Quando a força alcançou , o corpo de prova de madeira mostrado na figura falhou sobre cisalhamento ao longo da superfície indicada pela linha tracejada. Determine a tensão de cisalhamento média ao longo daquela superfície no instante da falha.
Passo 1
O exercício quer saber a tensão de cisalhamento média na superfície indicada pela linha tracejada, que é a superfície que estava resistindo ao cisalhamento antes da peça falhar.
Para encontrar a tensão de cisalhamento média, vamos nos lembrar de sua fórmula:
Da fórmula, temos que para encontrar o valor de na superfície indicada no instante da falha, devemos encontrar primeiro:
- A força cortante interna resultante nessa superfície no instante da falha;
- A área dessa superfície.
O esforço interno no instante da falha é igual à força , como mostra o Diagrama de Corpo Livre e a análise das condições de equilíbrio na imagem abaixo:
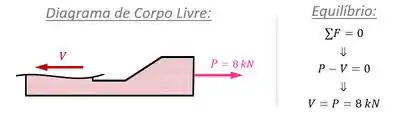
Já a área é retangular e pode ser calculada a partir da espessura do bloco de madeira e do comprimento da superfície.
Passo 2
Começando pelo cálculo da área retangular que se encontrava sob cisalhamento até a peça falhar:
Passo 3
Como já identificamos o esforço interno e a área , podemos substituir esses valores na fórmula da tensão cisalhante média:
Para que tenhamos um resultado em , podemos reescrever a força de como :