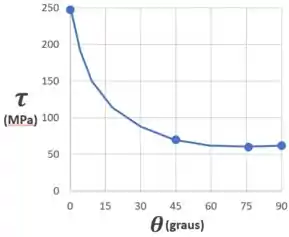
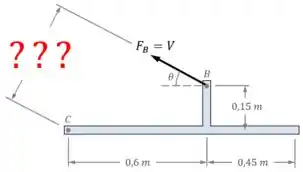
A estrutura está sujeita a carga de . Determine a tensão de cisalhamento média no parafuso em em função do ângulo da barra . Represente essa função em gráfico para e indique os valores de para os quais essa tensão é mínima. O parafuso tem diâmetro de e está sujeito a cisalhamento simples.
Passo 1
A tensão de cisalhamento média no parafuso vai ser dada pela equação de sempre:
A área será encontrada através do diâmetro do parafuso.
Mas e a força cisalhante interna ?
O parafuso está sobre cisalhamento simples, o que significa que a força cisalhante interna no parafuso é igual à força que uma peça da estrutura faz na outra no ponto .
Podemos encontrar o valor de analisando as condições de equilíbrio da peça inferior da estrutura. Para isso, vamos precisar de um DCL (Diagrama de Corpo Livre) dessa peça:
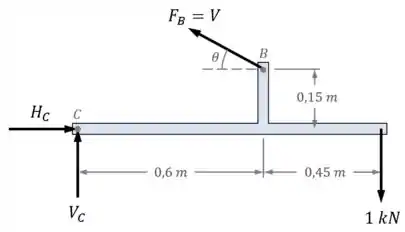
No caso, é o equilíbrio de momentos em relação ao ponto que vai nos permitir relacionar a força com a carga de .
Dessa forma, vamos encontrar o valor de em função do ângulo e, consequentemente, poderemos encontrar a tensão em função do ângulo .
Finalmente, para representar o gráfico de em função de e encontrar os valores de para os quais a tensão é mínima, vamos precisar usar um pouco de cálculo.
Passo 2
Vamos começar então pelo DCL da peça inferior da estrutura:
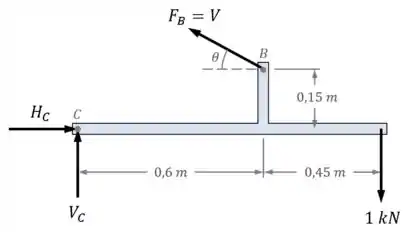
Vamos lembrar... As condições de equilíbrio que podemos aplicar nesse são:
- equilíbrio de forças (que podem ser horizontais ou verticais);
- e equilíbrio de momentos (que precisa ser em relação a algum ponto).
Nesse caso, não precisamos descobrir o valor das reações horizontal e vertical no apoio em , e . A nossa incógnita de verdade é a força , que queremos encontrar em função do ângulo .
Isso significa que o equilíbrio de momentos em relação ao ponto vai ser o suficiente para as nossas necessidades:
Para fazer esse equilíbrio de momentos, vamos nos lembrar de uma coisa: O momento gerado por uma força é igual à essa força vezes o seu braço .
Calcular o braço de uma força inclinada como é difícil:
Mas fica fácil se a gente decompor em suas componentes horizontal (que vai ter um braço de ) e vertical (que vai ter um braço de ):
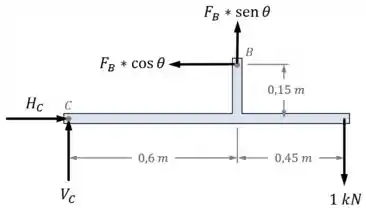
Feita a decomposição, agora podemos voltar para o equilíbrio de momentos:
Simplificando essa expressão:
Isolando :
Ainda podemos simplificar essa expressão!
Como todos os números são múltiplos de :
Como :
Passo 3
encontrado, agora vamos encontrar o valor da área .
O pino possui uma seção transversal circular de diâmetro , então podemos usar a formula da área circular em função do diâmetro:
Passo 4
Aplicando a fórmula da tensão cisalhante média:
Substituindo os valores encontrados:
Para ter resultados em , podemos reescrever como :
Passo 5
Precisamos e descobrir para quais valores de a tensão é mínima.
Vamos observar a expressão que encontramos para :
Essa expressão vai ser mínima quando a expressão for máxima.
Mas como vamos conseguir descobrir para que valores de a expressão é máxima?
Se lembrarmos de Cálculo 1, vamos nos lembrar que o máximo e mínimo das funções acontecem quando a sua derivada é igual a zero:
Vamos lembrar mais um pouco de C1!
Derivada de seno é cosseno e derivada de cosseno é menos seno, então essa derivada fica assim:
Agora temos que isolar :
Usando a função ou da sua calculadora:
Ou seja, ou é mínimo ou é máximo quando .
Passo 6
Ainda precisamos descobrir se é máximo ou mínimo quando .
Mas também precisamos esboçar um gráfico da tensão em função de .
Então vamos aproveitar para fazer as duas coisas ao mesmo tempo, calculando o valor de para alguns valores de :

Com esses valores, confirmamos que é mínimo quando e conseguimos fazer o esboço do gráfico de em função de :