O guindaste sobre esteiras equipado para demolição está se deslocando a uma velocidade constante de quando é subitamente parado. Calcule o ângulo máximo por meio do qual o cabo da bola de demolição oscila.
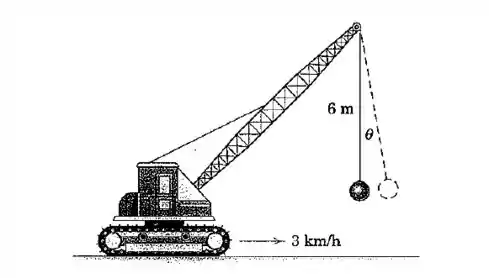
Passo 1
A bolinha está se deslocando com uma velocidade de Quando o guindaste parar, a bolinha irá subir:
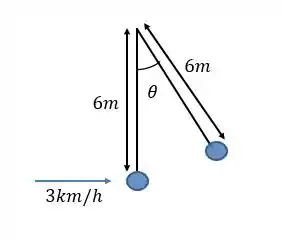
A força que estará atuando nesse sistema e exercendo trabalho será a força peso, que será contrária ao movimento, ou seja, o seu trabalho será negativo.
Passo 2
Quanto vale a altura que a bolinha sobe em função de
Basta você perceber que se é igual ao lado adjacente do triângulo e que é o valor do comprimento total, a altura vai ser a diferença entre esses valores:
Assim:
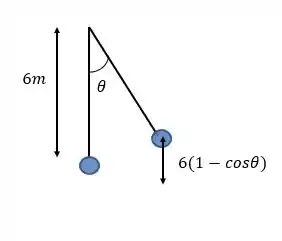
Passo 3
Basta a gente aplicar o teorema trabalho energia agora:
No estado a bolinha está em repouso. Além disso o trabalho é negativo:
Vamos converter a velocidade para
Passo 4
Assim:
Assim: