Introdução a Máquinas de Fluxo
Produzido por Raphael EloiTeoria
Classificação de Máquinas de Fluxo
Fala, galerinha! Tudo tranquilo pra começar nosso novo tópico? Então se alonga aí na cadeira e bora aprender um pouco sobre máquinas de fluxo!
Esse termo “Máquina de Fluxo” é meio feio, não é mesmo? Mas o conceito geral é bem simples! Uma máquina de fluxo nada mais é do que um equipamento que pode adicionar ou retirar energia de um fluido.
A gente já viu que um fluido perde energia ao escoar por tubulações e ao passar por “acidentes”, como válvulas, bifurcações e joelhos. Essa energia tem a ver com a pressão do fluido e chamamos a diminuição da pressão ao longo do escoamento de perda de carga.
Então, se o fluido tá sempre perdendo pressão e eu quero que ele continue escoando até um certo lugar, preciso adicionar energia em algum ponto do escoamento pra que ele chegue até o destino, né? Eu faço isso por meio de uma máquina de fluxo! Ela vai aumentar a pressão do fluido até um valor suficiente para gerar o escoamento até onde eu quero.
Dependendo do estado físico desse fluido, a gente usa diferentes equipamentos para se adicionar energia, por exemplo:
- Para líquidos: utilizamos as famosas bombas.
- Para gases: podemos usar ventiladores (baixo aumento de pressão), sopradores (médio aumento de pressão) ou compressores (alto aumento de pressão).
Dá uma olhadinha na imagem de alguns desses equipamentos:
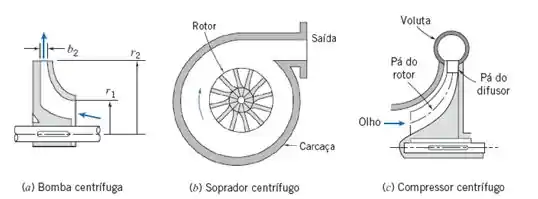
Parecem ser complicados, não é mesmo? Mas não são, a gente vai conseguir entender juntos o papel deles! ^^
Bom, mas eu te falei que também existem máquinas que retiram energia do fluido, não é mesmo? Essas são as turbinas!
Quando o fluido se choca com as pás de uma turbina, ele perde parte de sua energia para poder movimentar essas pás, ou seja, ele realiza trabalho (de rotação) sobre a turbina.
Maneiro, mas a gente vai focar mais no sistema de fluxo positivo, que adicionam energia ao sistema, basicamente vendo o funcionamento das bombas.
Equação de Euler para Turbomáquinas
A gente já viu as equações do balanço de massa, de quantidade de movimento linear (Navier-Stokes), de quantidade de movimento angular e de energia.
Já que a gente percebeu que o fluido rotaciona nas bombas e turbinas, o balanço da quantidade de momento angular será o mais importante aqui no nosso estudo!
Então, bora lá! Recordar é viver! O balanço da quantidade de movimento angular é dado por:
Matematicamente, isso tudo aí é essa equação aqui:
“É com essa equação que a gente vai analisar as turbomáquinas?” Calma, pequeno gafanhoto! A gente ainda vai simplificar bastante coisa! Vamos as simplificações:
Bom, essa é a descrição da nossa equação. Ela será a componente do torque, que está relacionada ao atrito e a pressão, somada com o campo gravitacional e com o torque do eixo aplicado ao sistema, isso tudo é igual a soma da variação da quantidade de movimento no tempo com o fluxo de quantidade de movimento angular pela superfície de controle, ok?
: Se refere a componente do torque que está relacionada com ao atrito e a pressão, e comparando essa componente do torque com o torque devido à rotação esse termo se torna desprezível.
: trata da força de campo gravitacional. Como o volume de controle é simétrico, esse termo vai se cancelar.
: trata do torque aplicado pelo sistema, podendo ser positivo (se for uma bomba, pelo fluido estar recebendo trabalho) ou negativo (se for uma turbina, pelo fluido estar exercendo trabalho). Esse vai continuar na equação, não tem jeito! haha
: trata da variação da quantidade de movimento angular ao longo do tempo. Como a gente vai tratar de regimes estacionários, esse termo também se anula.
: trata do fluxo da quantidade de movimento angular através da superfície de controle. Então, ele é bem importante e se mantém na equação.
Fazendo essas simplificações temos:
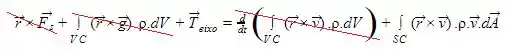
E chegamos à importante equação de Euler:
E o que essa equação diz pra gente? Ela diz que:
“Ao aplicarmos um torque no sistema (bombas), observamos uma variação da quantidade de movimento angular do fluido, ou o contrário, variações na quantidade de movimento angular produzem torque (turbinas). ”
Antes da gente dar uma desmembrada nessa equação, é importante a gente ver umas informações que vão nos ajudar…
Pensando no caso de uma bomba, o fluido entra nela, como mostrado abaixo:
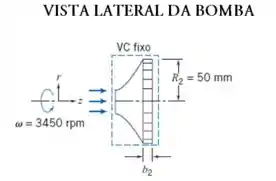
Ou seja, o fluido entra através da superfície do rotor e sai pela superfície mais externa da pá sofrendo uma rotação. Dá uma olhada nessa segunda imagem que esclarece melhor as coisas:
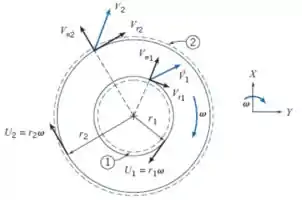
A superfície do rotor é essa superfície e a superfície mais externa da pá, é a superfície , show?
Em resumo, o que acontece no sistema é o seguinte: o fluido entra pelo rotor na posição onde , com uma velocidade (com componentes normal e tangencial) e sai pela superfície mais externa, onde , com velocidade (com componentes normal e tangencial).
O volume de controle está representado pelas linhas tracejadas, partindo da região e acabando na região , belezinha?
Voltando agora para a equação de Euler, podemos reescrevê-la em relação ao eixo de coordenadas , o eixo do rotor, desse jeito aqui:
Relacionando torque e vazão mássica
Vamos dar uma relembrada aqui na equação da vazão mássica que a gente viu nos outros tópicos? Ela era definida na forma infinitesimal como:
Opa! Esse termo está aparecendo na equação do torque, né? Então vamos substituir a definição de vazão mássica na expressão do torque, ficaremos com:
Olha só!! Parece que simplificamos mais ainda! *-*
Superfície de controle
Bom, é chegado o momento da gente analisar mais de perto essa superfície de controle, ok?
Se aplicarmos as condições de velocidade nas duas superfícies de controle, (entrada de fluido) e (saída de fluido), teremos:
Vamos usar o maiúsculo para indicar a velocidade, ok?
Como e não dependem da vazão mássica (), podemos resolver as integrais facilmente e ficamos com:
Pronto! Essa é a expressão do torque numa turbomáquina com entrada axial! A gente vê aí que o torque do eixo é responsável por gerar a componente tangencial da velocidade!
Potência do sistema ()
A gente define a potência do sistema () como sendo:
Em que é a velocidade angular de rotação no equipamento e é o torque de eixo. Ótimo! Como a gente já achou uma expressão para o , podemos substituir nessa equação, assim teremos:
Por convenção a gente pode chamar as velocidades tangenciais da velocidade do rotor de e , e sendo a velocidade tangencial dada pelo produto entre a velocidade angular e o raio, podemos escrevê-las como:
e
Nossa equação da potência, ficará com essa cara aqui, então:
Beleza!
Carga do fluido teórica ()
Por último, definimos uma propriedade bem importante! A carga do fluido teórica, é dada por:
Com ele a gente pode caracterizar bombas e turbinas da seguinte maneira:
- Se : a máquina é denominada de fluxo motriz (ou seja, são turbinas)
- Se : a máquina é denominada de fluxo operatriz (ou seja, são bombas ou ventiladores)
Agora, bora exercitar um pouco o que aprendemos, grande mestre!