Extensão de Funções
Produzido por Carolina SabaTeoria
Pessoal, estamos nos preparando para o grande momento desse assunto que é a série de Fourier. Antes de chegar lá veremos alguns conceitos introdutórios bem necessários. O primeiro é como realizar a extensão de uma função.
Mas antes precisamos revisar 3 conceitos: funções periódicas, funções pares e funções impares.
Funções periódicas
Olha pra a função :
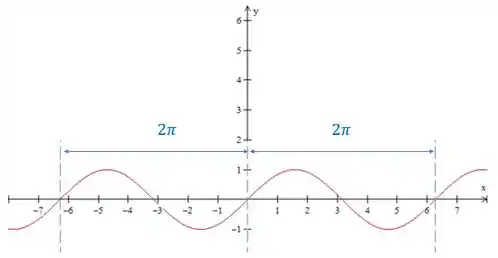
Repara que a função se repete a cada intervalo de tamanho de . Temos aí uma função periódica, uma função que se repete, seguindo sempre o mesmo padrão.
Podemos definir o período de uma função como o menor tamanho de um intervalo em para o qual uma função se repete. Assim, neste exemplo, ele vale . E dizemos que para essa função:
Ou seja, ela tem o mesmo valor para dois pontos separados por em . Se a função tem período , então:
Funções pares
Cara, já reparou que algumas funções são simétricas em relação ao eixo ? Tipo ?
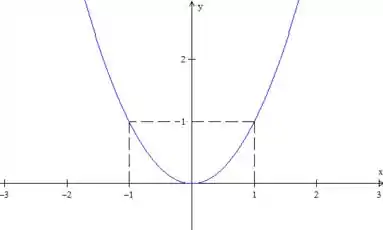
Tem como a gente ver se uma função é simétrica em relação a sem fazer o gráfico?
Olha para , vê que para , ela vale , e para , ela vale também. Temos
Vale também que
Ou seja, isso vale para qualquer
E boa notícia: Isso vale para todas as funções simétricas em relação a !
E essas funções são tão importantes que as chamamos de funções pares. Então, falou de função par, você vai lembrar que para ela vale que
Funções ímpares
Temos também as primas das funções pares: as funções ímpares. Por exemplo, a :
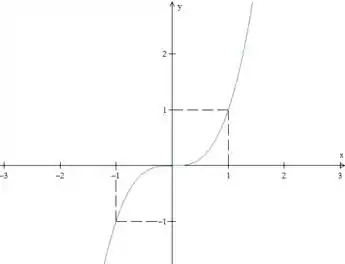
Por que elas são primas? Porque para desenhar uma função ímpar, como a nossa, a gente pode desenhar só o lado direito, espelhar esse lado em relação a (parte verde), e depois espelhar o resultado em relação a (parte azul abaixo do eixo ), assim:
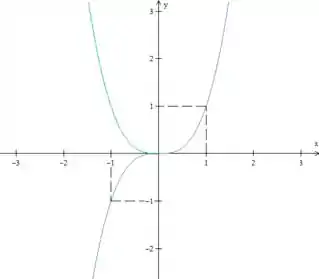
E aí a nossa curva fica sendo só a parte azul mesmo. Mesma pergunta do item anterior: A gente consegue descobrir se uma função é ímpar sem o gráfico dela?
Cara, repara que para , temos que e , ou seja, a gente pode escrever:
E isso, de novo, vale para qualquer , e para qualquer função que a gente consiga esboçar da forma que mostramos anteriormente:
Temos então que essa é a definição de funções ímpares.
Extensão de Funções
Cara, já temos a base necessária. Agora vamos ver o que é uma extensão de uma função. Imagina que temos , . O gráfico dela é assim:
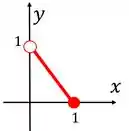
Se a gente quisesse criar uma função par a partir dessa, o que a gente faria? A gente pode espelhar ela em relação a , né? Fica assim:
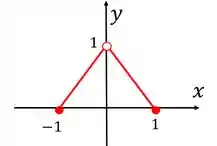
E se quisesse criar uma função ímpar? A gente só precisaria espelhar essa parte nova em relação a :
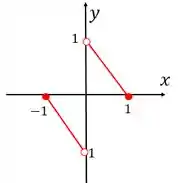
Acabamos de criar extensões para a função . A ideia de extensão é a gente pegar uma função e criar a partir dela uma função par, que vamos chamar de extensão par, ou uma função ímpar, que vai ser uma extensão ímpar de .
Agora, eu te pergunto: Como a gente vai achar as expressões dessas extensões? Vem descobrir!
Extensão Par
Vamos usar nosso exemplo
A gente já tem o gráfico, mas queremos a expressão da extensão par dessa função. Ela vai ser uma função definida por partes, certo?
O primeiro intervalo é , e nele a definição é a que já temos mesmo, isso não muda. O outro intervalo precisa ser simétrico a esse em relação a . Então vai ser , ok?
Falta a expressão da função para esse intervalo novo. Como a gente faz? Cara, é uma função par, certo? Então vale que
Temos que , né? Então podemos substituir nessa expressão, e achar outra expressão para :
Essa é a expressão que faltava. Nossa função fica
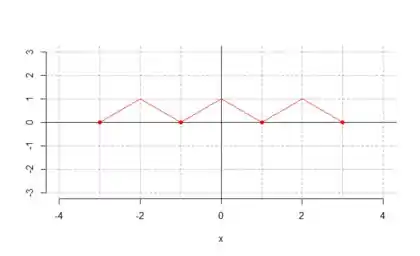
Essa é a extensão par de . Podemos também fazer a extensão par periódica dessa função. É só adicionar à definição da função a simbologia de função periódica.
Nossa função está dentro de um intervalo de tamanho 2, certo? Para fazer uma função periódica, é só repetir os valores de a cada período de tamanho .
O gráfico dessa extensão está mostrado abaixo
De forma geral, para fazer uma extensão par periódica de uma função de intervalo , fazemos
Extensão Ímpar
Agora para fazer a expressão da extensão ímpar da função , , vamos criar outra expressão, também para o intervalo simétrico .
Vai ser o mesmo esquema da anterior, vamos usar a definição de função ímpar
Temos que , então:
E
Então:
Agora, precisamos dizer que a função tem período se a gente quiser a extensão ímpar periódica dessa função, ou seja, escrevemos
Vou colocar o gráfico aqui para você dar uma olhada:
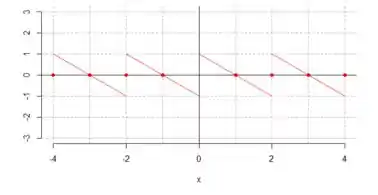
De modo geral, a extensão ímpar periódica de uma função de intervalo é:
Agora partiu exercícios! 😊