Trabalho Virtual
Produzido por Pablo RicardoTeoria
Introdução
Fala, pessoal!!! Se eu te perguntar: Qual é o ângulo que deixa essas barras em equilíbrio?
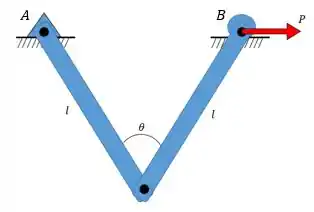
Para responder essa pergunta temos que fazer o diagrama de corpo livre. Para esta etapa é importante notar que é um apoio de 2° gênero, ou seja, possui forças de reação (uma vertical e uma horizontal), enquanto é um rolete possuindo apenas uma reação (na vertical). Lembre-se que é uma força externa que puxa o apoio (que rola né? Não é um rolete? rs).
Aí fica assim:
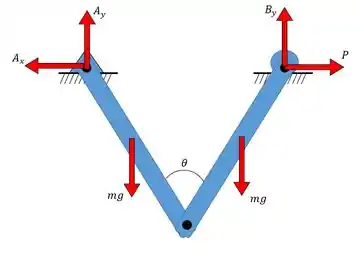
Como visto no capítulo de Equilíbrio, temos que fazer e para achar as reações. Depois, temos que separar as barrinhas e considerar todas as forças que atuam em cada barra.
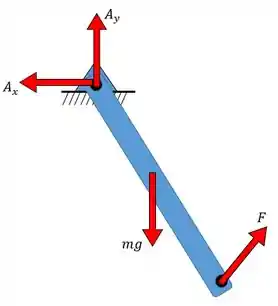
Feito isso, temos que fazer o equilíbrio toooodo de novo para essa barrinha e finalmente encontrar o ângulo . Parece trabalhoso né? E se eu te falar que tem um método mais rápido de resolver esses tipos de problemas?

Senhoras e senhores, apresento a vocês o Trabalho Virtual. Utilizamos esse método para resolver aquelas questões onde temos vários elementos interligados em que o movimento de um altera o movimento do outro, ou seja, podemos ter diferentes posições de equilíbrio no sistema.
Mas antes de começarmos, vamos fazer uma breve revisão de trabalho de uma força.
Trabalho de uma Força
Uma força aplicada a um corpo produz trabalho quando provoca um deslocamento. Vamos imaginar uma força empurrando uma caixa e produzindo um deslocamento :
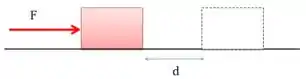
Repare que quando empurro a caixa, o seu movimento e a força estão na horizontal, ou seja, estão na mesma direção. Sempre que a força estiver na mesma direção do deslocamento que está sendo realizado, temos que o trabalho , será:
Em outras palavras o trabalho é o produto escalar entre a força e o deslocamento.
Mas e se a força aplicada não estiver no mesmo sentido do deslocamento? Nesses casos, temos que decompor a força e usar a componente que estiver paralela ao deslocamento.
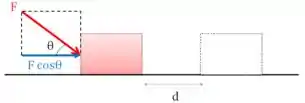
Não se esqueça de que trabalho é energia, então sua unidade é em Joule . Além disso, trabalho é uma grandeza escalar.
Agora, que já relembramos trabalho vamos introduzir um conceito de trabalho um pouco diferente. Vamos lá!
Trabalho virtual
A gente viu que para existir trabalho precisa existir deslocamento, certo? Mas os problemas que vemos em Estática estão parados.
A ideia do trabalho virtual é criarmos um movimento imaginário que vamos chamar de deslocamento virtual . E o que seria isto? É um movimento fictício que vamos obrigar o sistema a realizar para vermos as várias posições que ele pode assumir e determinarmos a mais correta.

Imagina uma bolinha que esteja em equilíbrio devido a atuação de várias forças. Para mover essa bolinha temos que aplicar uma nova força, certo? Para que o trabalho seja infinitesimal (virtual) é necessário haver também uma distância infinitesimal. Mas se eu quiser produzir um movimento muito muito pequeno, seria preciso uma força igualmente pequena, né?
A idéia é que ao criar essa força extra necessária para produzir o tal movimento infinitesimal, ela seja tão pequena que não altere em nada o conjunto de forças que já atuam no sistema, ou seja, ela vai ser desprezível.

Boa, Rubinho...Com base nessa ideia, podemos descrever o trabalho virtual realizado sobre a bolinha por esse tal deslocamento imaginário:
Uma vez que temos um deslocamento infinitesimal teremos uma variação infinitesimal do trabalho.
Diagrama de Forças Ativas
Lembra dos exercícios de Equilíbrio, onde tínhamos que fazer o diagrama de corpo livre para resolver as questões? Agora vamos fazer um diagrama um pouquinho diferente. Mas antes temos que ver alguns conceitos.
Para isso, vamos utilizar esse exemplo inicial para entendermos melhor.
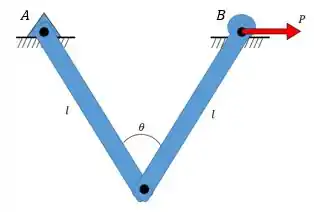
- Forças Ativas: são aquelas que estão aplicadas no corpo e que podem gerar trabalho virtual, ou seja, que podem produzir algum possível movimento. E como faço para identificar essas forças? É só ver quais das forças provocariam algum movimento na estrutura.
- Forças Reativas: são as forças que atuam nos apoios. Essas forças não realizam trabalho, pois a finalidade do apoio é impedir o movimento em uma ou mais direções.
- Forças internas: Essas forças sempre existem em pares iguais e de sentidos opostos (ação e reação), por isso, também não realizam trabalho. No nosso exemplo, temos um par dessas forças devido a conexão entre as barrinhas no ponto .
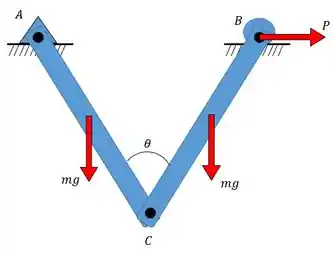
Imagina que a conexão do ponto pudesse se mover. Repare que tanto a força como as forças iriam fazer as barrinhas se moverem, logo elas são as nossas forças ativas.
No nosso exemplo, temos duas forças reativas em , porque não há movimento na horizontal e na vertical, isso acontece por que o apoio é um apoio de 2º gênero (dá pra ver isso, por que o símbolo do apoio é um triângulo fixo.
E temos uma única força em , pois não pode ter movimento na vertical, isso acontece por que é um apoio de 1º gênero (o símbolo dele é um círculo).
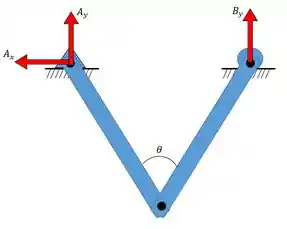
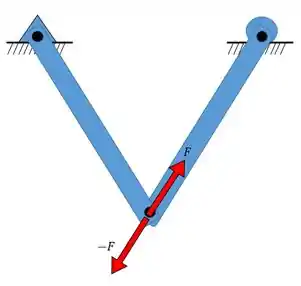
Agora que sabemos esses conceitos, podemos entender o diagrama de forças ativas. Nesse carinha desenhamos a estrutura principal do problema e colocamos apenas as forças que podem realizar trabalho virtual, ou seja, as forças ativas.
Então, como ficaria o diagrama do nosso exemplo?
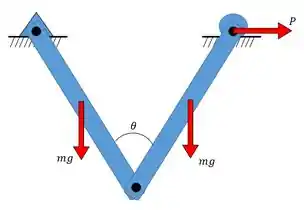
Para terminarmos de resolver esse exemplo só precisamos de mais um conceito. Aguenta aí.
Princípio do Trabalho Virtual
O Princípio do Trabalhos Virtual, que podemos abreviar por PTV, diz que o somatório dos trabalhos virtuais produzidos por cada força ativa em um sistema é nulo. Matematicamente, temos:
Nesse caso, é o trabalho virtual total.
Resumidamente, nas questões de trabalho virtual você terá que seguir esse passo a passo aqui:
1. Identificar todas as forças que podem gerar algum movimento na estrutura e montar o diagrama de forças ativas.
2. Calcular o trabalho que cada uma dessas forças faz.
3. Somar o trabalho virtual total e igualar a zero.
Agora que aprendemos isso tudo, você deve estar se perguntando qual é a vantagem de usar trabalho virtual.
– Você não precisa desmembrar toda a estrutura, você trabalha com ela inteira.
– Podemos resolver as questões sem precisar achar as forças reativas, o que economiza um tempo.
Então, bora terminar de resolver aquele exemplo para acabar com qualquer dúvida.
Sempre vamos começar as questões de trabalho virtual montando o diagrama de forças ativas. O diagrama desse exemplo nós já montamos, lembra?
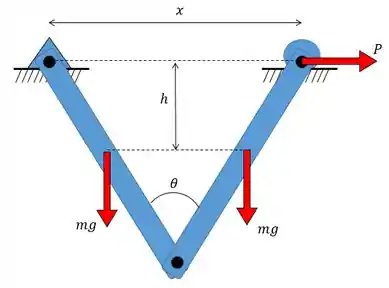
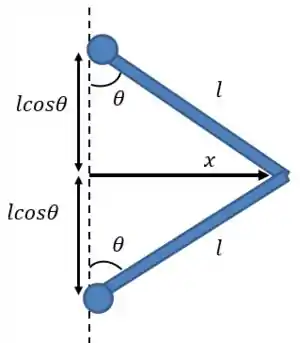
Depois temos que analisar quais são os movimentos possíveis de ocorrer devido cada força que identificamos. A gente chamou a distância entre os apoios de e a altura entre o centro de gravidade de cada barra até a linha dos apoios de . Que tal escrevermos esses valores em função de e ? Para isso vamos olhar o seguinte triângulo formado:
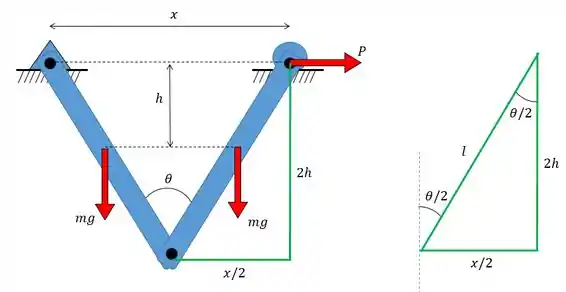
Como a figura é simétrica temos que a base do triângulo é metade da distância e o ângulo é metade do ângulo . E como o centro de gravidade das hastes é exatamente no meio vamos ter que a altura é .
Agora vamos para os trabalhos temos que a força pode fazer um deslocamento horizontal e os pesos , um deslocamento vertical. Escrevendo matematicamente isso, vamos ter o trabalho da força :
E o trabalho das forças peso:
Somando tudo vamos ter:
Por que o trabalho é igual a zero? Porque é um trabalho virtual se lembra? Ele deve ser nulo!
Sabemos que a questão pede o ângulo para haver equilíbrio. Mas repare que nessa equação não aparece nenhum ângulo , né? Então, o próximo passo é fazer aparecer a incógnita que queremos achar nessa equação aí.
Para isso, vamos achar alguma relação de e com o nosso . E como vamos fazer essa mágica? Vamos usar trigonometria.
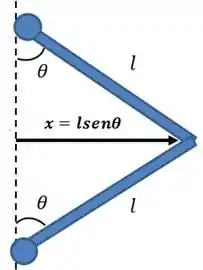
Utilizando o nosso triângulo:
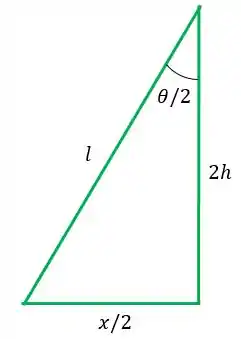
Fazendo o cosseno e seno desse triângulo, temos, para o seno:
Para o cosseno:
Lembra que falamos sobre o deslocamento virtual ser infinitesimal? Então...Vamos calcular esse deslocamento infinitesimal através do conceito de derivada, tá bom? ![]()
O próximo passo é derivar essas duas equações que achamos em função de para acharmos esses deslocamentos virtuais infinitesimais. Pessoal, lembrem que temos de derivar a função dentro do parêntesis também, isso faz com que aparece o termo , que é a derivada do ângulo.
Lembra de aplicar a regra da cadeia e que a derivada de cosseno é .
Agora para a altura:
Dessa vez a gente também aplicou a regra da cadeia mas com a derivada do seno que é .
Agora vamos substituir e naquela equação de
Calma não se assuste, podemos simplificar essa nossa equação dividindo por :
Como queremos saber o ângulo , temos que arrumar um jeito de isolar ele na fórmula:
Beleza, pessoal. Vamos colocar a mão na massa para pegar o jeito!
Trabalho virtual
Diagrama de Forças Ativas
Princípio do Trabalho Virtual
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 296, 7/1
Determine, em função do ângulo , o momento , aplicado através do eixo à conexão inferior, necessário para suportar a carga . Despreze os pesos das partes.
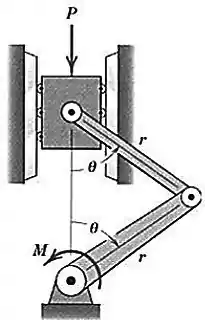
Passo 1
Temos duas coisas que exercem trabalho no sistema: A força e o momento
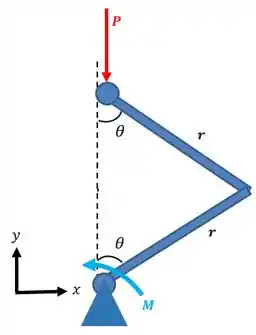
A força tem uma tendência a diminuir o comprimento , então seu trabalho é negativo:
E o momento tem uma tendência a diminuir o ângulo, então seu trabalho também é negativo:
Passo 2
Perceba que o comprimento é:
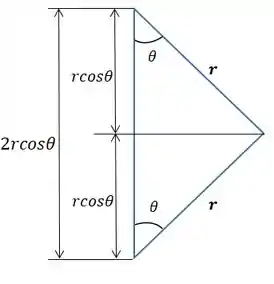
Precisamos derivar isso aí em função de :
Assim, o trabalho da força é:
Passo 3
Agora vamos usar o Princípio do Trabalho Virtual que diz que o somatório do trabalho virtual de cada força deve ser zero:
Como queremos saber o momento , teremos que:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 296, 7/2
A prensa trabalha por meio de um mecanismo de cremalheira e pinhão, e é usada para gerar grandes forças, tais como as necessárias para produzir encaixes por pressão. Se o raio médio das engrenagens do pinhão vale , determine a força que pode ser gerada pela prensa para uma dada força na manopla.
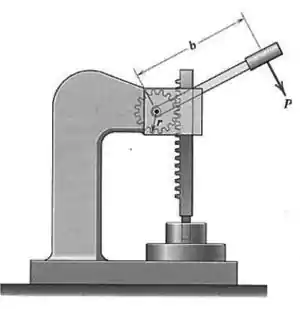
Passo 1
Temos que saber que o trabalho virtual total de todas as forças tem que ser nulo:
Então, vamos calcular o trabalho virtual de cada uma das forças e depois somá-los.
Passo 2
Se a manopla exerce uma força na superfície, a superfície exercer uma força na manopla, não é mesmo?
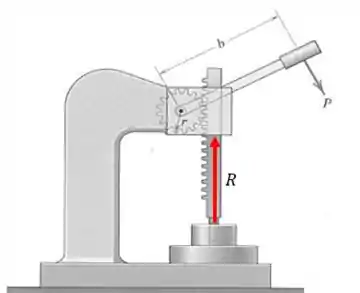
Na própria figura podemos ver que a força se encontra a uma distância do centro da engrenagem, então o seu trabalho virtual será:
E a força se encontra a uma distância do centro da engrenagem, logo seu trabalho virtual é:
Repare que eles têm sinais contrários, pois produzem momentos contrários!!!
Passo 3
Agora vamos somar esses dois momentos:
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 297, 7/10
O cilindro hidráulico é usado para afastar as conexões e elevar a carga Determine a força compressiva no cilindro, para a posição mostrada. Despreze a massa de todas as partes, à exceção de
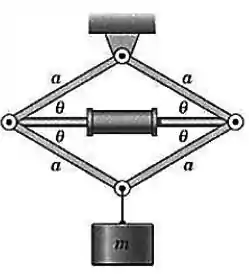
Passo 1
Repare que a estrutura formada pelas barrinhas comprime o cilindro, então o cilindro faz a seguinte força na estrutura:
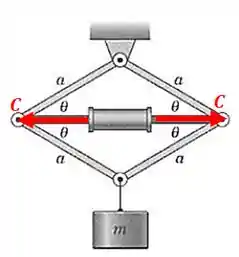
Mas isso tudo é causado pela a ação do peso:
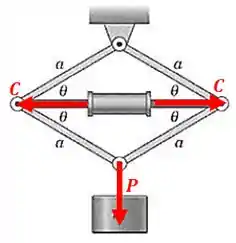
Passo 2
Vamos primeiro calcular o trabalho das forças
O comprimento que cada uma distende é dado por:
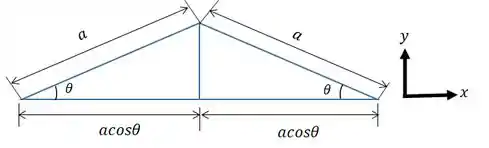
Como temos duas forças, vamos ter que:
Agora temos que derivar o comprimento em função de :
Então, vamos ter que:
Passo 3
Já o comprimento que o peso estica é dado por:
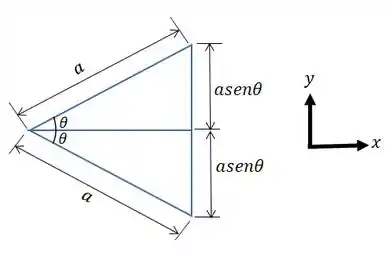
Pera, mas pela figura dá pra ver que ele vai esticar o negócio em cima e embaixo, assim:
Então, o trabalho da força peso é:
Agora precisamos derivar a comprimento em função de :
Então, temos que:
Passo 4
Sabemos que a soma do trabalho virtual de cada força deve ser zero:
Como queremos saber a força compressiva:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 296, 7/6
Cada uma das conexões uniformes do conjunto tem massa e comprimento A posição de equilíbrio do conjunto, no plano vertical, é determinada pelo binário , aplicado à conexão da esquerda. Expresse em função de
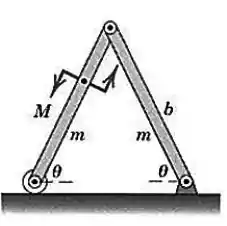
Passo 1
Para achar o ângulo de equilíbrio, vamos ter que primeiro calcular o trabalho virtual de cada força e depois usar o princípio do trabalho virtual:
Passo 2
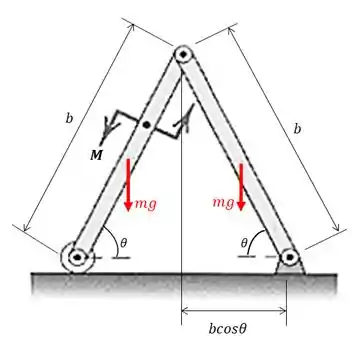
Perceba que a distância do ponto de aplicação da força peso, de ambas as barras, até o chão vale .
O trabalho virtual valerá:
E é negativo já que exibe uma tendência a diminuir a distância .
Mas como são duas barras, temos duas forças peso:
Passo 3
Já o trabalho virtual do momento pode ser escrito por:
Positivo já que o momento, por estar girando no sentido anti-horário que é o sentido natural de crescimento dos ângulos, tende a aumentar o ângulo. Assim:
Uma vez que , temos então:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 297, 7/8
A mola de constante não está distendida quando . Obtenha uma expressão para a força necessária para defletir o sistema de um ângulo A massa das barras é desprezível.
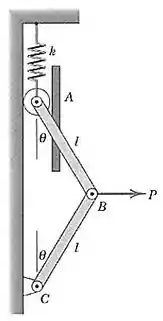
Passo 1
Vamos usar o princípio dos trabalhos virtuais:
Neste caso, temos duas forças: a força da mola () e a força
Podemos esquematizar isso assim:
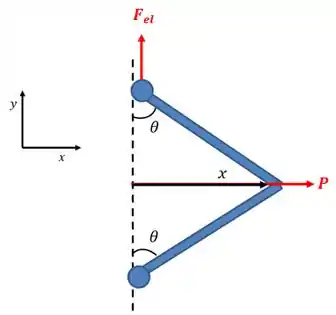
Repare que a força elástica está na direção , então vamos ter que o trabalho virtual da força elástica é:
Considerando:
A força elástica está fazendo com que y diminua, por isso seu trabalho é negativo.
Já a força está na direção , e fazendo com que aumente, então o trabalho da força é:
Passo 2
Beleza, agora precisamos melhorar a descrição do nosso sistema. A força elástica é dada por:
Quanto vale
Bom, pense no seguinte: se não houvesse , a barra ficaria totalmente esticada:
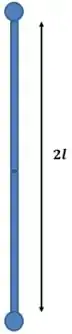
Com a força , o sistema fica assim:
Como a mola está conectada na parte circular superior, ela teve que se deslocar, certo?
Esse deslocamento será o comprimento máximo que a barra pode ter quando está esticada que é de menos o comprimento inicial que é :
Sendo assim, a força elástica será dada por:
Passo 3
Mas para achar o trabalho virtual da força elástica temos que derivar a equação de em função de :
Assim:
Passo 4
E o trabalho da força
Quanto vale Bem, basta olhar os triângulos desenhados antes.
Então, a derivada de em função de é:
Assim:
Passo 5
Agora vamos ter que a soma dos trabalhos virtuais deve ser nula:
Vamos cortar e arrumar isso aí:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 297, 7/9
Por meio de um mecanismo de cremalheira e pinhão, grandes forças podem ser desenvolvidas pelo saca-rolhas mostrado. Se o raio médio das engrenagens do pinhão vale 12 mm, determine a força que é exercida sobre a rolha para as forças dadas, , nas manoplas.
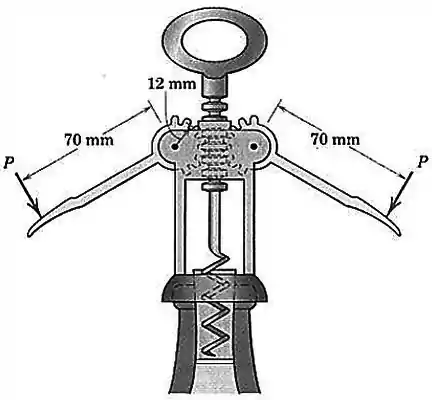
Passo 1
O nosso sistema acima pode ser representado assim:
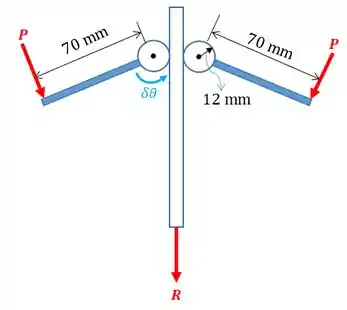
Passo 2
Perceba que a força está afastada do centro da engrenagem, então o seu trabalho é:
Já a força está afastada do centro da engrenagem, então o seu trabalho virtual é:
Mas repare que a força faz a engrenagem girar no sentido contrário ao movimento provocado pela força , então seu trabalho será negativo:
Esse aparece porque estamos lidando com um movimento de rotação da engrenagem!!!
Passo 3
Agora vamos aplicar o princípio dos trabalhos virtuais que diz que o somatório do trabalho que cada força produz deve ser zero:
Não esqueça que temos duas forças , então:
Como queremos determinar , vamos ter que:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 299, 7/22
Calcule a eficiência com a qual a cunha, com inclinação de , eleva o peso , sob a ação da força horizontal atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale
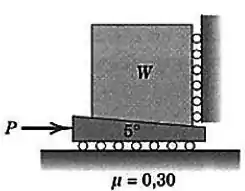
Passo 1
A eficiência será calculada por:
Qual será a força de entrada, que fornece o trabalho recebido? A força , que é a força que usamos como fonte de trabalho.
E qual é a força de saída, que gera o trabalho realizado? A força peso, já que vai ser ela que vai levantar o peso
Passo 2
Vamos analisar a cunha:
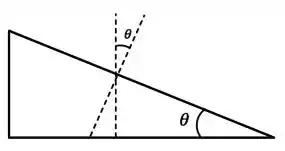
Entendeu a relação angular? Fizemos isso algumas vezes no capítulo anterior. Bem, o que falta? Falta a resistência que o peso exerce na cunha. Lembrando do ângulo de atrito fica assim:
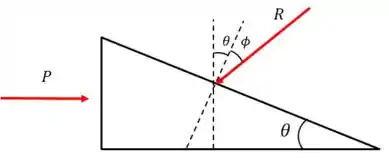
Precisamos achar as componentes horizontal e vertical da força :
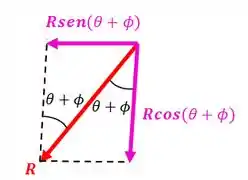
Pelo equilíbrio horizontal, teremos:
E pelo equilíbrio vertical temos:
Repare que a força de reação que a cunha exerce na caixa tem o mesmo módulo, mas sentido contrário à força representada.
Repare também que essa força tem uma componente vertical que equilibra o peso.
Passo 3
Agora, podemos escrever:
E:
Qual é a relação entre e? A mesma encontrada para e. Como a cunha é um triângulo retângulo:
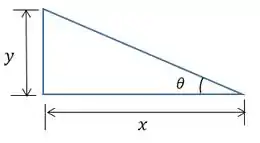
Assim, escreveremos:
Passo 4
Sendo assim:
Aqui temos que lembrar que o cálculo do ângulo de atrito é:
E é o ângulo da cunha que vale:
Então, a eficiência será:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2010, 201, 7/33
Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em . As conexões são articuladas à estrutura do caminhão em , e . Determine a força fornecida pelo cilindro para sustentar a plataforma na posição mostrada. A massa da plataforma e das conexões pode ser desprezada em comparação com a massa do caixote de com centro de massa em .
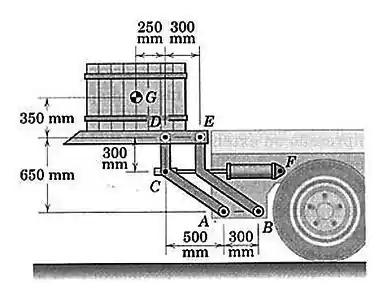
Passo 1
Vamos usar o princípio dos trabalhos virtuais:
Neste caso, temos duas forças: a força fornecida pelo cilindro e a força peso do caixote .
Podemos esquematizar isso assim:
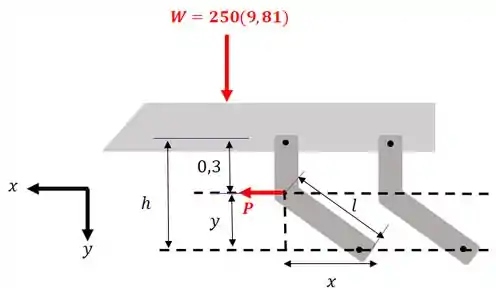
Repare que a força peso está no sentido positivo do eixo , então vamos ter que o trabalho virtual desta força é:
Já a força está no sentido positivo do eixo , então o trabalho da força é:
Passo 2
Beleza, agora precisamos melhorar a descrição do nosso sistema. A força peso é dada por:
Vamos analisar a geometria do nosso problema!
Pense no seguinte: a força garante que a plataforma fique exatamente na posição da figura. Então, vamos analisar este triângulo retângulo aqui:
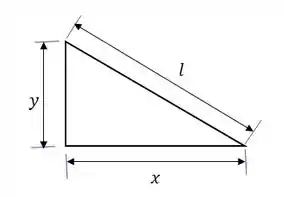
Temos que:
Se derivarmos isso, vamos ter que:
Passo 3
Então, o trabalho virtual da força peso vai ser:
Passo 4
Agora vamos ter que a soma dos trabalhos virtuais deve ser nula:
Vamos cortar e arrumar isso aí:
Agora é só substituirmos os valores de e conforme foi indicado na figura do enunciado:
Então: