Esforços Internos em Vigas
Produzido por Pablo RicardoTeoria
Introdução
Vamos dizer que na primeira questão da sua prova, você encontra o seguinte exercício:
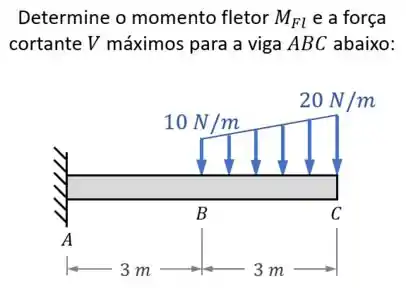
O que você faz?
Talvez você já tenha estudado como resolver esse tipo de exercício, ou na sua própria disciplina de Resistência dos Materiais, ou em uma disciplina de Mecânica ou Estática.
Nesse caso, você pode pular essa teoria e resfrescar a sua memória fazendo uns exercícios resolvidos! 😉
Mas caso você não tenha visto como resolver esse tipo de exercício, ou caso você queira re-estudar essa matéria, estamos aqui para aprender a resolvê-los! 👊
Isso porque o que esse exercício pede é basicamente a primeira e maior etapa da resolução de quase todos os exercícios de “flexão” e/ou “cisalhamento” em uma viga, que são exercícios que muito provavelmente vão cair na sua prova.
Então vamos lá!

Métodos da Estática
Basicamente, esse exercício que você viu aí em cima é um exercício de solicitação em vigas, em que o objetivo é determinar os esforços internos na viga (mais sobre eles depois!).
A boa noticia é que existe uma “receita” para resolver esses exercícios.
Essa receita consiste em 4 passos, que devem ser feitos um atrás do outro, que junto compõem o que chamamos de “métodos da estática”.
São eles:
- O diagrama de corpo livre;
- O equilíbrio;
- A análise dos esforços internos;
- E os diagramas de esforços internos.
Cada passo tem detalhes que precisamos aprender, então vamos ver eles um a um, começando pelo:
PASSO 1: Diagrama de Corpo Livre ou “DCL”
Nesse primeiro passo, o objetivo é trocar os apoios que existem na peça por reações (forças ou momentos aplicados na peça pelos apoios).
O primeiro tipo de apoio que existe é o engaste, que é o apoio que nós vimos no exemplo lá em cima:
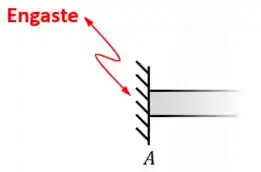
O engaste significa dizer que a peça está, naquele ponto, fixa a algo rígido (normalmente uma parede).
Um engaste em um certo ponto de uma peça faz 3 tipos de reações nela: um momento , uma força na vertical e uma força na horizontal .
Para o nosso exemplo de um engaste no ponto , por exemplo, devemos colocar as reações , e no lugar no engaste, deixando o diagrama de corpo livre assim:
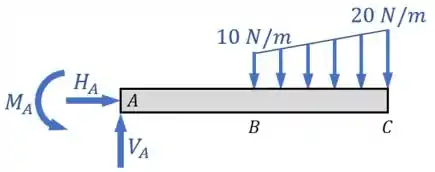
Por enquanto, a gente não conhece o valor numérico dessas reações, mas tentamos, se possível, já adivinharmos o seu sentido (para onde elas apontam) na hora de fazermos o DCL.
Os outros tipos de apoio que existem são o apoio fixo e o apoio móvel, exemplificados na viga abaixo:
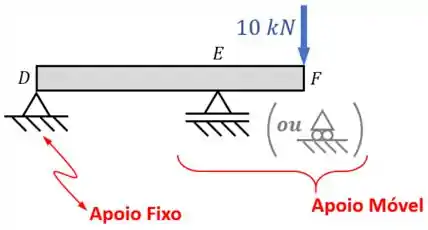
Os apoios fixos são como um pino, que fazem no ponto em que encostam na peça uma força na vertical e uma força na horizontal .
Para o apoio fixo em do exemplo acima, as reações ficam assim:
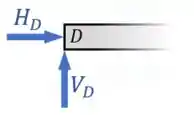
Já os apoios móveis são como plataformas deslizantes, que sempre só fazem na peça uma única reação: uma força sempre perpendicular ao chão.
Normalmente o chão é horizontal, e então a reação perpendicular ao chão é chamada de uma força na vertical . É o que acontece no apoio móvel em do nosso exemplo acima:
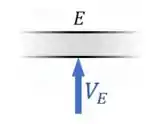
Mas, às vezes, o chão em um apoio móvel é inclinado. Nesse caso, a reação perpendicular ao chão deve ser chamada dessa forma mesmo, como no exemplo abaixo:
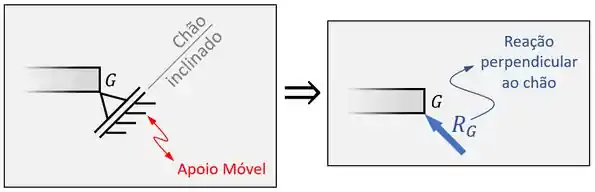
Aí...
Uma vez que você já tiver desenhado a sua peça com reações no lugar dos apoios (esse desenho é o tal diagrama de corpo livre da peça), você pode seguir para o:
PASSO 2: Equilíbrio
Aqui, o objetivo é aplicar as condições de equilíbrio na peça: equações que nos permitem descobrir quais são os valores necessários para as reações em uma peça para que essa peça fique em equilíbrio.
Existem 3 condições de equilíbrio que nós usamos, que são:
- O equilíbrio de forças na vertical, ;
- O equilíbrio de forças na horizontal, ;
- E o equilíbrio de momentos em relação à algum ponto da barra, .
Nessas três equações, nós temos sempre um somatório de forças ou momentos que devem ser iguais à zero.
Basicamente, o que essas equações estão dizendo é que a força resultante e o momento resultante na peça devem ser nulos.
Aí, para fazer esses somatórios, podemos trabalhar com forças e momentos igual trabalhávamos lá na física:
- O somatório de forças na vertical, por exemplo, pode ser feito somando as componentes verticais de todas as forças na peça, tendo em mente o sentido de cada uma;
- E o somatório de momentos pode ser feito somando os momentos já aplicados em uma peça com todos os momentos que as forças na peça geram em relação a um certo ponto escolhido, tendo em mente o braço de cada força.
Forças Distribuídas
Normalmente, a parte mais difícil dessa etapa de equilíbrio é trabalhar com forças distribuídas.
Elas são forças que agem ao longo de um dado comprimento, e, assim, tem unidades (newtowns por metro) ou similar, ao invés da unidade usual de uma força concentrada, que é (newtons).
Um exemplo é a força do nosso exemplo inicial, que ainda varia linearmente entre e ao longo de seu comprimento:
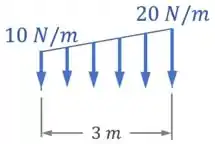
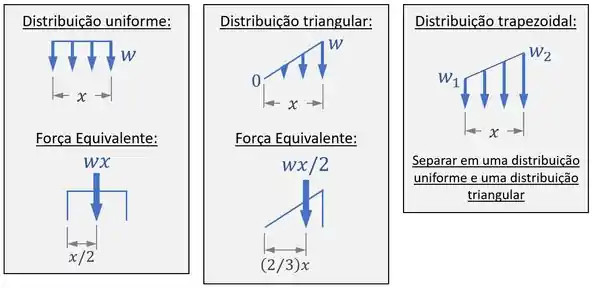
Aqui, o segredo é trocar a força distribuída “” por uma força equivalente (ou duas, no caso de uma distribuição trapezoidal), como mostra a imagem abaixo:
PASSO 3: Análise dos Esforços Internos
Depois de descobrir o valor das reações desconhecidas na sua peça através do equilíbrio, o próximo passo é a análise dos esforços internos.
Nela, o objetivo é descrever os esforços internos na sua peça: as forças e momentos que atuam dentro da peça, no material dela.
E como que a gente faz isso? 🤔
Fazendo seções na peça, desenhando os esforços que atuam nessas seções e aplicando o equilíbrio para descobrir o valor desses esforços.
Vamos entender isso por partes...
i. Fazendo seções na peça
Aqui, precisamos identificar todas as descontinuidades que existem na peça.
Uma descontinuidade pode ser o início ou o final da peça, uma força ou momento concentrado, ou o início ou final de uma força distribuída.
Na nossa viga , por exemplo, temos descontinuidades em , em e em :
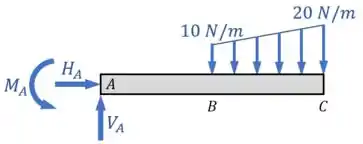
O que isso significa é que precisamos fazer seções entre esses pontos de descontinuidade.
Nesse exemplo acima, por exemplo precisamos fazer um desenho para analisar os esforços internos nas seções entre e e outro desenho para as seções entre e .
Aí, ao fazer essas “seções”, nós podemos escolher qual lado da viga queremos manter e qual lado da viga queremos descartar.
Se escolhermos manter o lado esquerdo da viga para as seções entre e e o lado direito da viga para as seções entre e , essas seções ficam assim:
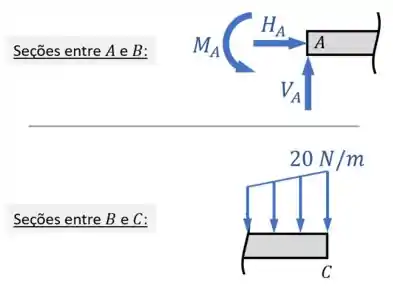
Agora, depois de fazer essas seções/desenhos acima, ainda precisamos definir um eixo (normalmente o eixo ) de referência e indicar os intervalos de para o qual aquele desenho vale:
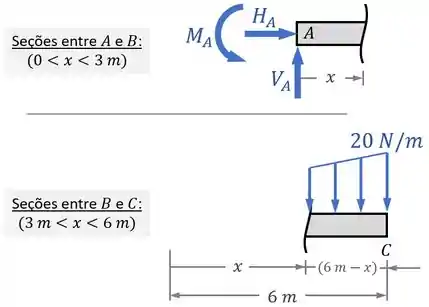
ii. Desenhando os esforços que atuam nessas seções
Aqui, nós vamos ter 3 tipos de esforços internos:
- A força normal , perpendicular à seção, que deve ser desenhada apontando para fora da peça:
- A força cortante , paralela à seção, que deve ser desenhada para cima quando estiver à esquerda da peça e para baixo quando estiver à direita, como se ela quisesse fazer a peça girar no sentido horário:
- E o momento fletor , que deve ser desenhado como se ele quisesse comprimir a parte superior da peça ou da viga e esticar a parte inferior:
![]()

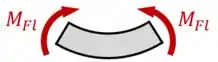
Dessa forma, os desenhos das nossas seções ficam assim:
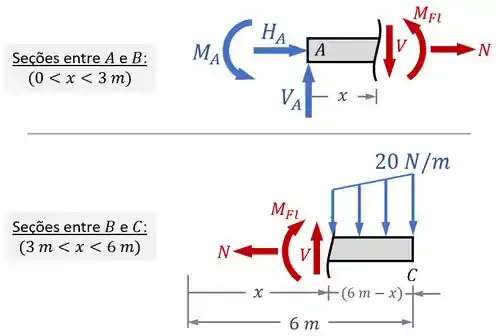
iii. Aplicando o equilíbrio para descobrir o valor desses esforços
Feitos os desenhos acima, a última etapa da análise dos esforços internos está em aplicar as condições de equilíbrio (, e ) para cada um desses desenhos.
Assim, vamos conseguir descrever o valor dos esforços internos , e na peça como funções , e da posição da seção em que esses esforços atuam.
PASSO 4: Diagramas de Esforços Internos ou “DEI”
Por fim, o último passo é pegar as funções , e que foram encontradas na análise dos esforços internos e plotar elas em gráficos chamados de diagramas de esforços internos.
Na hora de plotar esses gráficos, é importante verificar coisas como:
- O valor das funções , e no início e fim de cada intervalo de seções utilizados na análise dos esforços internos;
- A linearidade ou concavidade dessas funções;
- E os pontos críticos (pontos de máximo ou de mínimo) dessas funções.
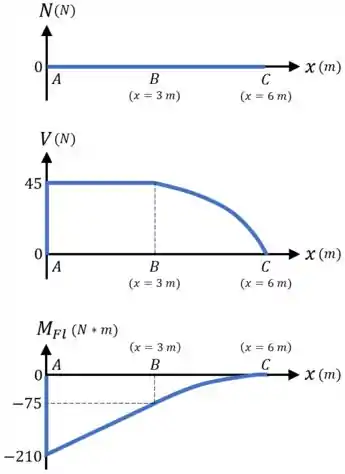
Se fosse para resolver o exercício do início por completo, os seus diagramas de esforços internos ficariam assim:
Finalização
Feitos os quatro passos acima, aí você consegue responder o que o exercício tiver pedido sobre os esforços internos na peça.
Para o exercício da viga , por exemplo, que queria saber o momento fletor e a força cortante máximas nessa viga, podemos recorrer aos diagramas de esforços internos acima.
Desses diagramas, vemos que o valor máximo, em termos absolutos, do momento fletor é e da força cortante é .
Agora...
Assim, na teoria, já dá pra entender um pouco como resolver esses exercícios.
Mas se você quiser ficar craque mesmo, aí é só fazer os exercícios resolvidos a seguir!