Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Coordenadas Cilíndricas

Ver Todos os Exercícios

Teoria

Oiii, Bem vindo ao Responde Aí! Bora aprender juntinhos como usar as Coordenadas cilíndricas!

Sistema de Coordenadas Cilíndricas

Você lembra das coordenadas polares? Se você não lembra, ou não conhece, tudo bem, você pode dar uma conferida aqui! As coordenadas cilíndricas são as coordenadas polares, mas tridimensionais!!

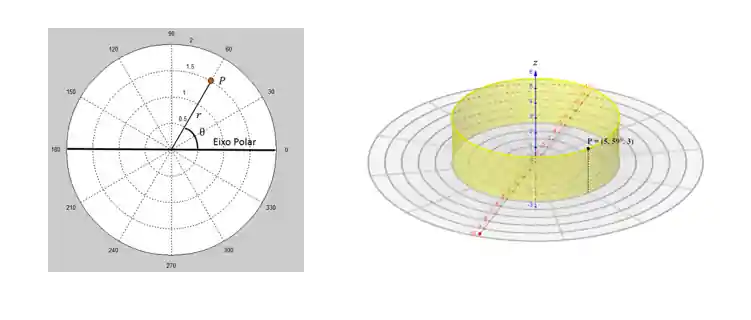
Coordenadas polares e cilíndricas.
Coordenadas polares e cilíndricas.

-Mas como assim?! 😖

Nas coordenadas cilíndricas a gente continua tendo as coordenadas e , mas agora, além dessas teremos a coordenada ! A figura ai em cima ajuda bastante a gente visualizar, a coordenada é uma velha conhecida nossa, ela é a mesma que a gente usa no sistema cartesiano.

-E como a gente pode representar um ponto nas coordenadas cilíndricas?

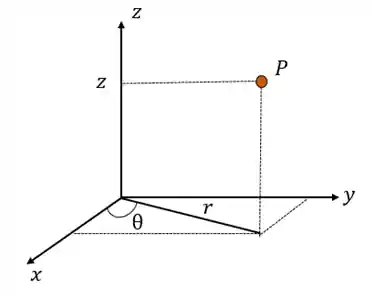
Ponto P em coordenadas cilíndricas.
Ponto P em coordenadas cilíndricas.

Ele é representado por . O sistema de coordenadas cilíndricas é muito útil quando a gente vai resolver integrais triplas, por exemplo!

📢 Clique para ver mais:

Quer aprender mais sobre coordenadas cilíndricas? Se liga nesse vídeo completaço, cheio de exemplos que o Responde Aí preparou pra você! 👇

Coordenadas Cilíndricas Para Coordenadas Cartesianas

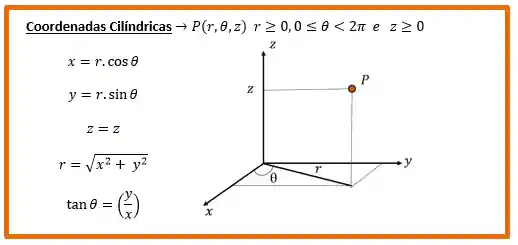
Na figura abaixo podemos ver as relações entre as coordenadas cartesianas e cilíndricas:

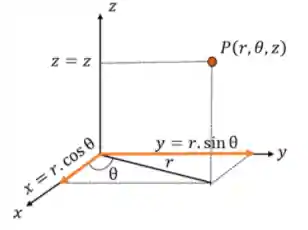
Coordenadas cilíndricas no sistema cartesiano.
Coordenadas cilíndricas no sistema cartesiano.

Temos então as seguintes relações:

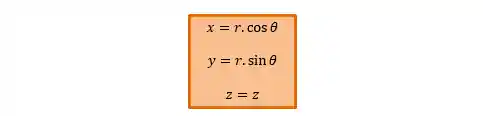
Relações entre coordenadas cartesianas e cilíndricas.
Relações entre coordenadas cartesianas e cilíndricas.

Mas e se quiséssemos transformar as coordenadas cartesianas em cilíndricas? Tudo que precisamos fazer é pegar as relações acima e colocar , e em evidência!

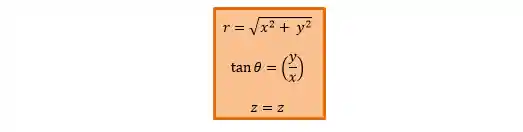
Relações entre coordenadas cartesianas e cilíndricas.
Relações entre coordenadas cartesianas e cilíndricas.

Pronto!! Já conhecemos mais um sistema de coordenadas!! Eu vou deixar pra você um resumindo com as relações das coordenadas cilíndricas!

Resumo das relações entre coordenadas cilíndricas e cartesianas.
Resumo das relações entre coordenadas cilíndricas e cartesianas.

Agora, vamos praticar com exercícios?!

Coordenadas Cilíndricas Para Coordenadas Cartesianas

Exercícios Resolvidos

Exercício Resolvido #1

Unicamp, Lista 3 – Geometria Analítica (MA141), 2014, pág 1, ex. 10

Encontre uma equação em coordenadas cilíndricas da superfície cuja equação em coordenadas cartesianas é dada:

  1. x 2 + y 2 + z 2 = 9 z

  2. x 2 + y 2 = 9

Passo 1

Vamos colocar em prática o que aprendemos sobre coordenadas cilíndricas na teoria!! Como queremos encontrar as equações em coordenadas cilíndricas vamos utilizar as seguintes relações:

x = r . cos ⁡ θ   ( 1 )

y = r . sin ⁡ θ     ( 2 )

z = z       3

x 2 + y 2 = r 2   ( 4 )

Bora, achar as equações!!

Passo 2

  1. x 2 + y 2 + z 2 = 9 z

    2. Pela relação (3), o z das coordenadas cartesianas é o mesmo das coordenadas cilíndricas, então não vamos mexer nele.

    Mas vamos precisar trocar o x 2     e o y 2 .

    Elevando as expressões (1) e (2) ao quadrado:

    x 2 = r 2 cos 2 ⁡ θ

    y 2 = r 2 s e n 2 θ  

    Substituindo na expressão dada:

    r 2 cos 2 ⁡ θ + r 2 s e n 2 θ + z 2 = 9 z

    r 2 cos 2 ⁡ θ + s e n 2 θ + z 2 = 9 z

    Opa, mas sabemos que:

    cos 2 ⁡ θ + s e n 2 θ = 1

    Então temos:

    r 2 + z 2 = 9 z

    r 2 + z - 9 2 2 = 81 4

    Essa foi rápida!! Uhuull!!

    Vamos para a próxima!!

    Passo 3

  2. x 2 + y 2 = 9

Substituindo a relação ( 4 ) , temos:

r 2 = 9

De curiosidade, essa é a expressão de um círculo de centro na origem e raio 3 .

Resposta

a )   r 2 + z - 9 2 2 = 81 4

b )   r 2 = 9

Exercício Resolvido #2

Unicamp, Lista 3 – Geometria Analítica (MA141), 2014, pág 1, ex. 11

Encontre uma equação em coordenadas cartesianas da superfície cuja equação em coordenadas cilíndricas é dada:

  1. r = 3 cos ⁡ θ

  2. z 2 sin ⁡ θ = r 3

Passo 1

Agora, temos as expressões em coordenadas cilíndricas e queremos achar as expressões em coordenadas cartesianas.

Passo 2

  1. Temos a expressão r = 3 cos ⁡ θ e queremos obtê-la em coordenadas cartesianas. Para isso, vamos usar as seguintes relações:

    2. r = x 2 +   y 2   ( 1 )

    x = r cos ⁡ θ → cos ⁡ θ = x r → cos ⁡ θ = x x 2 +   y 2     ( 2 )

    z = z       ( 3 )

    Substituindo as relações ( 1 ) ,   ( 2 ) e ( 3 ) na expressão do enunciado, temos:

    r = 3 cos ⁡ θ →   x 2 +   y 2 = 3 cos ⁡ θ   ( 4 )

    Assim, substituindo a relação ( 5 ) em ( 4 ) , temos:

    x 2 +   y 2 = 3 x x 2 +   y 2

    Rearanjando a expressão:

    x 2 +   y 2 = 3 x

    x - 3 2 2 + y 2 = 9 4

    Chegamos na expressão que queríamos. O enunciado não nos pediu para identificar a cônica, mas por motivo de curiosidade essa é a expressão de uma cíircunferência de centro C 3 2 ,   0 e raio r = 3 2 .

    Passo 3

  2. z 2 sin ⁡ θ = r 3

Fazendo o mesmo passo a passo do item anterior e utilizando as relações 1 ,   ( 2 ) e ( 3 ) e além dessas:

sin ⁡ θ = y x 2 +   y 2

Vamos substituir as relações na equação que nos foi dada:

z 2 sin ⁡ θ = r 3

z 2 y x 2 +   y 2 = ( x 2 +   y 2 ) x 2 +   y 2

Rearranjando a expressão, temos:

z 2 y = ( x 2 +   y 2 ) 2

Prontinho!! Chegamos na expressão que queríamos!!

Resposta

a )   x - 3 2 2 + y 2 = 9 4

b )   z 2 y = ( x 2 +   y 2 ) 2

Exercício Resolvido #3

Lista Unicamp – Geometria Analítica (MA141)pág 1, ex. 495

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por:

x 2 + y 2 + 4 z 2 = 16

Passo 1

Vamos relembrar as relações entre coordenadas cilíndricas e cartesianas!

x = r c o s θ

y = r s i n θ

z = z

Belezinha, agora vamos substituir na equação do enunciado!

r c o s θ 2 + r s i n θ 2 + 4 z 2 = 16

r 2 ( cos 2 ⁡ θ + sin 2 ⁡ θ ) + 4 z 2 = 16

r 2 + 4 z 2 = 16

Prontinho!!

Resposta

r 2 + 4 z 2 = 16

Exercício Resolvido #4

Lista Unicamp – Geometria Analítica (MA141) pág 1, ex. 498

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por:

x 2 + y 2 = 9

Passo 1

Vamos relembrar as relações entre coordenadas cilíndricas e cartesianas mais uma vez!

x = r c o s θ

y = r s i n θ

z = z

Show de bolinhas, agora vamos substituir na equação do enunciado!

r c o s θ 2 + r s i n θ 2 = 9

r 2 ( cos 2 ⁡ θ + sin 2 ⁡ θ ) = 9

Lembrando que cos 2 ⁡ θ + s i n 2 θ = 1

r 2 = 9

Eitcha! Isso aí faz total sentido, já que sabemos que x 2 + y 2 = 9 é a equação de um círculo centrado na origem, cujo r a i o = 3 . Muito maneirinho, né não?!

Resposta

r 2 = 9

Exercício Resolvido #5

Lista Unicamp – Geometria Analítica (MA141) pág 1, ex. 496

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por:

x 2 - y 2 = 3 z 2

Passo 1

Vamos relembrar as relações entre coordenadas cilíndricas e cartesianas mais uma vez!

x = r c o s θ

y = r s i n θ

z = z

Show de bolinhas, agora vamos substituir na equação do enunciado!

r c o s θ 2 - r s i n θ 2 = 3 z 2

r 2 cos 2 ⁡ θ - sin 2 ⁡ θ = 3 z 2

Lembrando que c o s 2 θ = cos 2 ⁡ θ - s i n 2 θ

r 2 c o s 2 θ = 3 z 2

Prontinho!!

Resposta

r 2 c o s 2 θ = 3 z 2