União, Soma e Interseção de Subespaços Vetoriais
Produzido por Bruno PestanaTeoria
União de Subespaços Vetoriais
Eaí, se fizermos a união de dois subespaços, ainda teremos um subespaço?
Bom, primeiro temos que lembrar qual a definição de união de conjuntos né haha. Se liga:
Opa, traduzindo o matematiquês teríamos: O conjunto A união com B e compostos por elementos que pertencem a A ou a B. Então para algum elemento pertencer à união de dois conjuntos basta ele pertencer a um dos conjuntos, é isso? Exatamente!
Então voltamos a pergunta, essa união é um subespaço?
E agora que vem o pulo do gato. Se pegarmos um vetor e outro vetor , com e subespaços vetoriais.
Pelo que eu falei ali em cima, como então , do mesmo jeito, já que então . Se for um subespaço vetorial, então ele deve ser fechado para soma, lembra? Logo, , concorda?
Bom, se e , então Não conseguiu visualizar?
Imagine que o subespaço fosse um plano e uma reta que atravessa esse plano. Portanto, e :
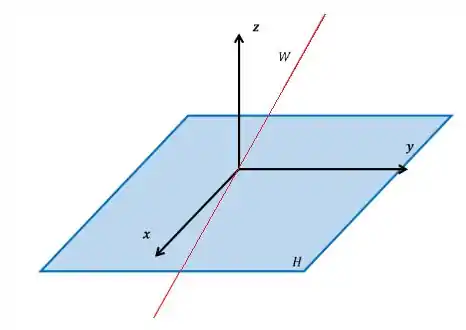
Vamos acrescentar os vetores e
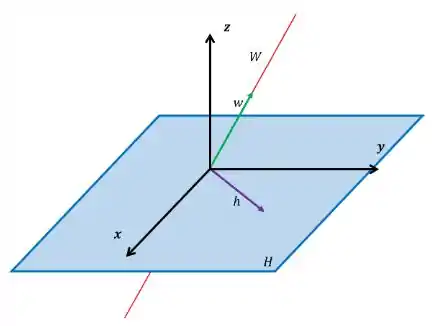
Queremos analisar a soma desses vetores pois para ser um espaço vetorial, então tem que pertencer a .
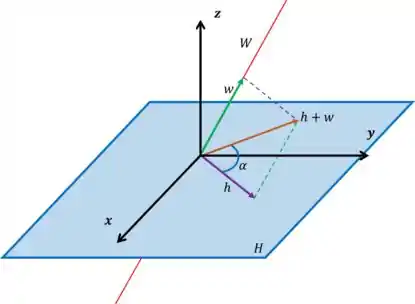
E, como podemos ver, sob essas condições, não é um subespaço vetorial, pois não está fechado para a soma. O vetor claramente não pertence à nem à .
Mas, por exemplo, se a reta estivesse contida no plano , teríamos . Logo, seria um subespaço!
Tente imaginar a reta contida inteiramente do plano. Assim, todos os vetores da reta estariam no plano. Ao somarmos um vetor de (do plano) com um vetor de (que faz parte do plano) obteríamos um vetor que também estaria no plano!
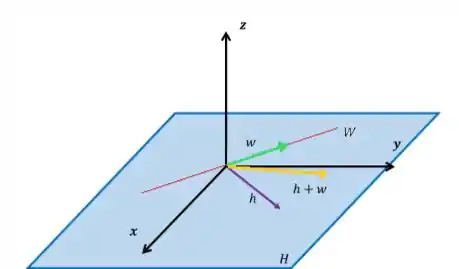
Perceba, então, que depende da ocasião. Não podemos generalizar se é subespaço vetorial. Ele será um subespaço se ou .
Soma de Subespaços Vetoriais
Beleza, e a soma de subespaços? Gerará um subespaço vetorial? Não? Ou não podemos afirmar nada? Bom, primeiro temos que entender o que é a soma de subespaços!
Primeira coisa que vocês têm que por na cabeça é que não tem nada a ver com união! É bem comum confundir as duas e até achar que significam a mesma coisa, mas vocês nunca vão cometer esse erro, porque foram avisados haha.
Quando nós somamos dois conjuntos e , nós somamos todos os elementos de , com todos os elementos de ! Ou seja:
Novamente traduzindo o matematiquês, significa que o conjunto formado pela soma de W e H é formado pelos elementos y tal que sendo que pertence a H e pertence a W. Então os elementos de não são mais elementos de ou , mas a combinação linear de todos os elementos desses subespaços.
Opa, então podemos escrever a soma de dois conjuntos como o conjunto gerado pela junção dos geradores dos dois conjuntos.

Mas em?
Calma, deixa eu explicar melhor. Por exemplo, se e , então . Sacou?
No caso da figura lá de cima, é um reta do , e é um plano do . Logo, !! Se liga:
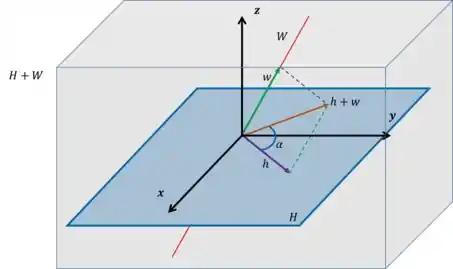
Obs: Vale lembrar que nesse caso porque e ! Se, por exemplo, a reta estivesse contida no plano , teríamos que , beleza?
Na figura acima, fica claro que está contido em ! E isso não foi coincidência, é algo que sempre vai acontecer! Se e são subespaços de , então também será subespaço vetorial de .
Base da Soma de Subespaços
Bom, acabamos de ver que a soma de dois subespaços sempre será um subespaço. Sendo assim, seria interessante se soubéssemos como achar a base dessa soma não acham? E na verdade é bem simples! Lembrando do que eu falei agora pouco:
“Se e , então .”
Opa, se é um gerador de , então para acharmos uma base basta tirarmos os elementos do meio!
E fim de papo galera.
Interseção de Subespaço Vetorial
Já aprendemos a unir e a somar subespaços. Agora só falta interseção né galera? Bom, vamos ver como fica.
A primeira coisa que temos que ver é como escrever a interseção de dois conjuntos:
Esse novo conjunto é formado por todos os elementos do espaço onde está contido que satisfazem as duas condições ao mesmo tempo.
Lembra que na união de conjuntos era necessário satisfazer pelo menos uma delas? Então, na interseção ele tem que satisfazer ambas. Bem intuitivo né? Ficaria algo assim:
Momento tradução: O conjunto A intersecção com B é formado pelos elementos x tal que x pertence a A e também pertencem a B
Agora que já sabemos achar a interseção, temos aquela pergunta clássica, a interseção de dois subespaços também é um subespaço vetorial?
Vamos ver esses conjuntos aqui embaixo:
Será que a interseção desses dois subespaços do também é subespaço do ?
Vamos por passos:
Passo 1: Pra podermos definir bem o subconjunto gerado pela interseção dos subespaços precisamos das condições deles. A do ta fácil:
Mas e a do ? Do jeito que tá, tá complicado de ver né. Bom, vamos passar para a forma cartesiana então:
Portanto, temos o sistema:
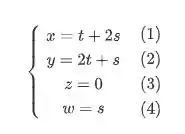
De temos:
Substituindo e em :
Beleza, agora temos as condições dos dois conjuntos:
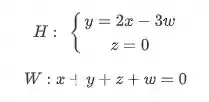
Passo 2: Agora vamos ver qual o conjunto de vetores que satisfaz ambas as condições ao mesmo tempo. Para isso, é só montarmos um sistema com as equações que temos:
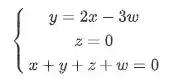
Substituindo as duas primeiras equações na última, obtemos:
Passo 3: Assim, podemos concluir que:
Opa, então os vetores que pertencem a tem essa cara:
Portanto,
Caraca, então conseguimos escrever a interseção como um ! Logo, este conjunto é um subespaço vetorial (lembre-se do teorema)!
Pera, então pegamos dois conjuntos que eram subespaços vetoriais e sua interseção deu também um subespaço! Será que isso sempre acontece? De fato, sim, e isso nos leva a mais um teorema:
