Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.3 - Ex. 21
21. Suponha que tenha o produto interno euclidiano. Em cada parte, use o processo de Gram-Schmidt para transformar a base numa base ortonormal e esboce os vetores de ambas as bases no plano .
(a)
(a)
Passo 1
(a) Pelo processo, primeiro vamos repetir o primeiro vetor:
Depois fazemos a projeção pra achar o segundo:
Fazendo o produto interno:
Calculando a norma:
Passo 2
Então:
Fazendo as continhaszzzzZzzzZzZ...
Para ser ortonormal:
Calculando a norma de
Então:
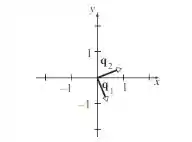
Passo 3
(a) Pelo processo, primeiro vamos repetir o primeiro vetor:
Depois fazemos a projeção pra achar o segundo:
Fazendo o produto interno:
Calculando a norma:
Passo 4
Então:
Fazendo as continhaszzzzZzzzZzZ...
Para ser ortonormal:
Calculando a norma de
Então:
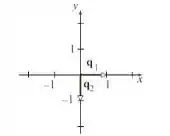
Resposta
(a)
(b)
Exercícios de Livros Relacionados
26. Suponha que o R 3 tenha o produto interno euclidiano. O subespaço de R 3 gerado pelos vetores u → 1 = 4 5 , 0 , - 3 5 e u → 2 = 0,1 , 0 é um plano passando pela origem. Expresse w → = 1,2 , 3 na f
25. Suponha que R 3 tenha produto interno u → , v → = u 1 v 1 + 2 u 2 v 2 + 3 u 3 v 3 Use o processo de Gram-Schmidt para transformar u → 1 = 1,1 , 1 ,u → 2 = 1,1 , 0 , u → 3 = 1,0 , 0 Numa base orton
22. Suponha que R 2 tenha o produto interno euclidiano. Em cada parte, use o processo de Gram-Schmidt para transformar a base u → 1 , u → 2 , u → 3 numa base ortonormal.(a)u → 1 = 1,1 , 1 , u → 2 = -
27. Repita o Exércício 26 com u → 1 = ( 1,1 , 1 ) e u → 2 = 2,0 , - 1 .
28. Suponha que R 4 tenha o produto interno euclidiano. Expresse o vetor w = - 1,2 , 6,0 na forma w = w 1 + w 2 , sendo w 1 um vetor no espaço gerado por u 1 = ( - 1,0 , 1,2 ) e u 2 0,1 , 0,1 , e w 2