1. Fala, galerinha! Preparados para mais uma questão? Então bora lá!

Como é paralelo a , então devemos ter uma proporcionalidade entre esses dois vetores. Isso pode ser escrito como

Por outro lado, ortogonal a , o que significa que o produto interno dos dois vetores é nulo. Assim, se considerarmos que , onde são constantes a serem determinadas, obtemos

Vamos reservar esse resultado para mais tarde.

Outra informação importante do enunciado é que deve ser uma soma de e , ou seja

Portanto,

Agora preste atenção no pulo do gato. Lembra daquele resultado do Passo 1? ? Então, vamos multiplicar a primeira equação acima por , a segunda deixamos como está e a terceira multiplicamos por . Depois somamos as três equações e, em um determinado momento teremos que pode ser eliminado por ser igual a zero. Então, ficamos só com uma equação para . Olha só:

Agora, somando as três equações, obtemos

Legal não é mesmo?

Agora que sabemos o valor de , podemos substituir no sistema de equações e obter as outras constantes:

Pronto, agora sabemos que

A figura com e está no enunciado da questão. Nesse caso, levamos em conta que é paralelo a enquanto é perpendicular. Além disso, usamos os módulos dos vetores e .

Passo 2

2. Para descobrir a área do paralelogramo, só precisamos multiplicar a largura do paralelogramo por sua altura. A largura é justamente o módulo do vetor, ou seja, . A altura é um pouco mais complicada porque temos que saber o ângulo entre os vetores e . Na figura abaixo, vemos que

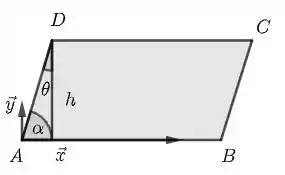
Por outro lado, o ângulo entre e é dado pela fórmula

Então, como , temos

Então, a altura vai ter a seguinte expressão:

Finalmente, a área do paralelogramo será